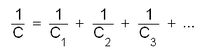This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കപ്പാസിറ്റന്സ്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (പുതിയ താള്: == കപ്പാസിറ്റന്സ് == == Capacitance == വൈദ്യുത ചാര്ജ് സംഭരിക്കാന് ക...) |
Mksol (സംവാദം | സംഭാവനകള്) (→Capacitance) |
||
| (ഇടക്കുള്ള 5 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 5: | വരി 5: | ||
== Capacitance == | == Capacitance == | ||
| - | വൈദ്യുത ചാര്ജ് സംഭരിക്കാന് കഴിയുന്ന ഒരു സംവിധാനത്തിലെ (കപ്പാസിറ്റര്) ചാര്ജും പൊട്ടന്ഷ്യലും തമ്മിലുള്ള | + | വൈദ്യുത ചാര്ജ് സംഭരിക്കാന് കഴിയുന്ന ഒരു സംവിധാനത്തിലെ (കപ്പാസിറ്റര്) ചാര്ജും പൊട്ടന്ഷ്യലും തമ്മിലുള്ള അനുപാതം. രണ്ടു ലോഹത്തകിടുകള് (പ്ലേറ്റുകള്) ഒരു പാരാവൈദ്യുത പദാര്ഥം (dielectric) കൊണ്ട് വേര്തിരിച്ച സംവിധാനത്തെയാണ് പൊതുവേ കപ്പാസിറ്റര് അഥവാ കണ്ടന്സര് എന്നു വിളിക്കുന്നത്. അതിന്റെ കപ്പാസിറ്റന്സ് രണ്ടു പ്ലേറ്റുകളും അഭിമുഖമായി വരുന്ന വിസ്തൃതി, അവ തമ്മിലുള്ള അകലം, പാരാവൈദ്യുതത്തിന്റെ സ്വഭാവം തുടങ്ങിയ ഘടകങ്ങളെ ആശ്രയിച്ചിരിക്കും (കപ്പാസിറ്റി എന്ന പേരാണ് മുമ്പ് ഉപയോഗിച്ചിരുന്നത്). |
| - | കപ്പാസിറ്ററിന്റെ പ്ലേറ്റുകളിലൊന്നിന് 'Q' ചാര്ജു നല്കിയാല് (മറ്റേ പ്ലേറ്റില് തുല്യ അളവില് വിപരീത ചാര്ജ് | + | കപ്പാസിറ്ററിന്റെ പ്ലേറ്റുകളിലൊന്നിന് 'Q' ചാര്ജു നല്കിയാല് (മറ്റേ പ്ലേറ്റില് തുല്യ അളവില് വിപരീത ചാര്ജ് പ്രേരിതമാകും) അതിന്റെ പൊട്ടന്ഷ്യല് 'V' അളവ് ഉയരുമെങ്കില് പ്രസ്തുത കപ്പാസിറ്ററിന്റെ കപ്പാസിറ്റന്സ് C = Q/V എന്നു നിര്വചിച്ചിരിക്കുന്നു. ഒരു നിശ്ചിതഘടനയുള്ള കപ്പാസിറ്ററിന്റെ കപ്പാസിറ്റന്സ് നിശ്ചിതമായിരിക്കും. |
| - | കപ്പാസിറ്റന്സിന്റെ ഏകകം ഫാരഡ് (Fared - f) ആണ്. 1 കൂളൂം ചാര്ജു നല്കുമ്പോള് ഒരു കപ്പാസിറ്ററിന്റെ പൊട്ടന്ഷ്യല് 1 വോള്ട്ട് ഉയരുമെങ്കില് അതിന്റെ കപ്പാസിറ്റന്സ് 1 ഫാരഡ് ആണെന്ന് പറയും. ഫാരഡ് വളരെ വലിയ ഏകകം ആകയാല് പ്രായോഗിക ആവശ്യങ്ങള്ക്ക് മൈക്രാഫാരഡ് | + | |
| - | ( | + | [[ചിത്രം:Vol6_317_1.jpg|200px]] |
| - | എന്ന സൂത്രവാക്യം ഉപയോഗിക്കാം. അതുപോലെ, കപ്പാസിറ്ററുകള് സമാന്തരമായി ബന്ധിച്ചാല് പരിണത കപ്പാസിറ്റന്സ്,C = | + | |
| + | കപ്പാസിറ്റന്സിന്റെ ഏകകം ഫാരഡ് (Fared - f) ആണ്. 1 കൂളൂം ചാര്ജു നല്കുമ്പോള് ഒരു കപ്പാസിറ്ററിന്റെ പൊട്ടന്ഷ്യല് 1 വോള്ട്ട് ഉയരുമെങ്കില് അതിന്റെ കപ്പാസിറ്റന്സ് 1 ഫാരഡ് ആണെന്ന് പറയും. ഫാരഡ് വളരെ വലിയ ഏകകം ആകയാല് പ്രായോഗിക ആവശ്യങ്ങള്ക്ക് മൈക്രാഫാരഡ് μ<sub>f</sub> = 10<sup>-6</sup>f) പൈകോഫാരഡ് (P<sub>f</sub> = 10<sup>-12</sup>f) എന്നീ ചെറിയ ഏകകങ്ങള് ആണ് ഉപയോഗിക്കാറ്. നിശ്ചിത കപ്പാസിറ്റന്സുള്ള ഒന്നിലേറെ കപ്പാസിറ്ററുകളെ അന്യോന്യം ബന്ധിപ്പിച്ച് ഒരു വൈദ്യുത പരിപഥത്തിനാവശ്യമായ പരിണത കപ്പാസിറ്റന്സ് സൃഷ്ടിച്ചെടുക്കാന് കഴിയും. ഉദാഹരണത്തിന്, C<sub>1</sub>, C<sub>2</sub>, C<sub>3</sub>..... എന്നിങ്ങനെ വ്യത്യസ്ത കപ്പാസിറ്റന്സുള്ള കപ്പാസിറ്ററുകള് ഒരു ശ്രണിയില് ബന്ധിച്ചാല് അവയുടെ പരിണത കപ്പാസിറ്റന്സ് C കാണാന് | ||
| + | |||
| + | [[ചിത്രം:Vol6_317_2.jpg|200px]] | ||
| + | |||
| + | [[ചിത്രം:Vol6_317_3.jpg|200px]] | ||
| + | |||
| + | എന്ന സൂത്രവാക്യം ഉപയോഗിക്കാം. അതുപോലെ, കപ്പാസിറ്ററുകള് സമാന്തരമായി ബന്ധിച്ചാല് പരിണത കപ്പാസിറ്റന്സ്,C = C<sub>1</sub> + C<sub>2</sub> + C<sub>3</sub>- + ...ആയിരിക്കും. ശ്രണീബന്ധനത്തില് പരിണത കപ്പാസിറ്റി കുറയുമെന്നും സമാന്തര ബന്ധനത്തില് കൂടുമെന്നും വ്യക്തം. രണ്ടുതരം ബന്ധനവും ഒന്നിച്ച് ഉപയോഗപ്പെടുത്തിയാണ് ആവശ്യമായ പരിണത കപ്പാസിറ്റി കൈവരിക്കുക. | ||
Current revision as of 10:52, 24 ഡിസംബര് 2014
കപ്പാസിറ്റന്സ്
Capacitance
വൈദ്യുത ചാര്ജ് സംഭരിക്കാന് കഴിയുന്ന ഒരു സംവിധാനത്തിലെ (കപ്പാസിറ്റര്) ചാര്ജും പൊട്ടന്ഷ്യലും തമ്മിലുള്ള അനുപാതം. രണ്ടു ലോഹത്തകിടുകള് (പ്ലേറ്റുകള്) ഒരു പാരാവൈദ്യുത പദാര്ഥം (dielectric) കൊണ്ട് വേര്തിരിച്ച സംവിധാനത്തെയാണ് പൊതുവേ കപ്പാസിറ്റര് അഥവാ കണ്ടന്സര് എന്നു വിളിക്കുന്നത്. അതിന്റെ കപ്പാസിറ്റന്സ് രണ്ടു പ്ലേറ്റുകളും അഭിമുഖമായി വരുന്ന വിസ്തൃതി, അവ തമ്മിലുള്ള അകലം, പാരാവൈദ്യുതത്തിന്റെ സ്വഭാവം തുടങ്ങിയ ഘടകങ്ങളെ ആശ്രയിച്ചിരിക്കും (കപ്പാസിറ്റി എന്ന പേരാണ് മുമ്പ് ഉപയോഗിച്ചിരുന്നത്).
കപ്പാസിറ്ററിന്റെ പ്ലേറ്റുകളിലൊന്നിന് 'Q' ചാര്ജു നല്കിയാല് (മറ്റേ പ്ലേറ്റില് തുല്യ അളവില് വിപരീത ചാര്ജ് പ്രേരിതമാകും) അതിന്റെ പൊട്ടന്ഷ്യല് 'V' അളവ് ഉയരുമെങ്കില് പ്രസ്തുത കപ്പാസിറ്ററിന്റെ കപ്പാസിറ്റന്സ് C = Q/V എന്നു നിര്വചിച്ചിരിക്കുന്നു. ഒരു നിശ്ചിതഘടനയുള്ള കപ്പാസിറ്ററിന്റെ കപ്പാസിറ്റന്സ് നിശ്ചിതമായിരിക്കും.
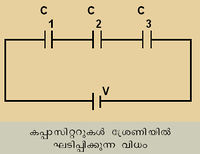
കപ്പാസിറ്റന്സിന്റെ ഏകകം ഫാരഡ് (Fared - f) ആണ്. 1 കൂളൂം ചാര്ജു നല്കുമ്പോള് ഒരു കപ്പാസിറ്ററിന്റെ പൊട്ടന്ഷ്യല് 1 വോള്ട്ട് ഉയരുമെങ്കില് അതിന്റെ കപ്പാസിറ്റന്സ് 1 ഫാരഡ് ആണെന്ന് പറയും. ഫാരഡ് വളരെ വലിയ ഏകകം ആകയാല് പ്രായോഗിക ആവശ്യങ്ങള്ക്ക് മൈക്രാഫാരഡ് μf = 10-6f) പൈകോഫാരഡ് (Pf = 10-12f) എന്നീ ചെറിയ ഏകകങ്ങള് ആണ് ഉപയോഗിക്കാറ്. നിശ്ചിത കപ്പാസിറ്റന്സുള്ള ഒന്നിലേറെ കപ്പാസിറ്ററുകളെ അന്യോന്യം ബന്ധിപ്പിച്ച് ഒരു വൈദ്യുത പരിപഥത്തിനാവശ്യമായ പരിണത കപ്പാസിറ്റന്സ് സൃഷ്ടിച്ചെടുക്കാന് കഴിയും. ഉദാഹരണത്തിന്, C1, C2, C3..... എന്നിങ്ങനെ വ്യത്യസ്ത കപ്പാസിറ്റന്സുള്ള കപ്പാസിറ്ററുകള് ഒരു ശ്രണിയില് ബന്ധിച്ചാല് അവയുടെ പരിണത കപ്പാസിറ്റന്സ് C കാണാന്
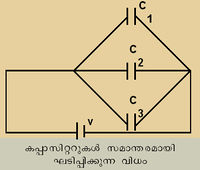
എന്ന സൂത്രവാക്യം ഉപയോഗിക്കാം. അതുപോലെ, കപ്പാസിറ്ററുകള് സമാന്തരമായി ബന്ധിച്ചാല് പരിണത കപ്പാസിറ്റന്സ്,C = C1 + C2 + C3- + ...ആയിരിക്കും. ശ്രണീബന്ധനത്തില് പരിണത കപ്പാസിറ്റി കുറയുമെന്നും സമാന്തര ബന്ധനത്തില് കൂടുമെന്നും വ്യക്തം. രണ്ടുതരം ബന്ധനവും ഒന്നിച്ച് ഉപയോഗപ്പെടുത്തിയാണ് ആവശ്യമായ പരിണത കപ്പാസിറ്റി കൈവരിക്കുക.