This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
അനിശ്ചിതത്വ തത്ത്വം
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
(→അനിശ്ചിതത്വ തത്ത്വം) |
Mksol (സംവാദം | സംഭാവനകള്) (→അനിശ്ചിതത്വ തത്ത്വം) |
||
| (ഇടക്കുള്ള 22 പതിപ്പുകളിലെ മാറ്റങ്ങള്‍ ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 2: | വരി 2: | ||
Uncertainty principle | Uncertainty principle | ||
| - | + | മൗലിക പ്രാധാന്യമുള്ള ഒരു ഭൌതികശാസ്ത്ര തത്ത്വം. 1927-ല്‍, ജര്‍മന്‍ ഭൌതികശാസ്ത്രജ്ഞനായ വെര്‍ണര്‍ ഹൈസന്‍ബര്‍ഗ് ആണ് ഈ തത്ത്വം അവതരിപ്പിച്ചത്. ഇതു സൂക്ഷ്മകണങ്ങളുടെ ക്വാണ്ടം സ്വഭാവത്തിന്റെ ഒരു പരിണതഫലമാണ്. | |
| - | ബലതന്ത്രത്തില്‍ ഒരു വസ്തുവിന്റെ അവസ്ഥയെ കുറിക്കുന്നതിന് (സ്ഥാനം, സംവേഗം), (ഊര്‍ജം, പ്രസ്തുത ഊര്‍ജാവസ്ഥയില്‍ സ്ഥിതിചെയ്യുന്ന സമയം) തുടങ്ങിയ ചര ജോഡികള്‍ പ്രധാനമാണ്. ഇവയെ വിഹിത ചരങ്ങള്‍ (canonical variables) എന്നു പറയും. സ്ഥൂലവസ്തുക്കളുടെ കാര്യത്തില്‍ വിഹിത ചരങ്ങളെ എത്ര കൃത്യതയോടെയും അളന്നു തിട്ടപ്പെടുത്താന്‍ കഴിയും. എന്നാല്‍ സൂക്ഷ്മകണങ്ങളുടെ കാര്യത്തില്‍ രണ്ടു ചരങ്ങളെയും ഒരേസമയം കൃത്യമായി നിര്‍ണയിക്കുക സാധ്യമല്ല എന്ന്അനിശ്ചിതത്വ തത്ത്വം അനുശാസിക്കുന്നു. ഉദാഹരണത്തിന്ഒരു കണത്തിന്റെ സ്ഥാനം 'x'-ഉം അതിന്റെ x ദിശയിലുള്ള സംവേഗം 'P<sub>x</sub>'-ഉം ആണെന്നിരിക്കട്ടെ. x അളക്കുന്നതില്‍ വരുന്ന പിശക് (error) 'Δx'-ഉം 'P<sub>x</sub>' അളക്കുന്നതില്‍ വരുന്ന പിശക് 'ΔP<sub>x</sub>'-ഉം ആണെങ്കില്‍ ഈ അനിശ്ചിതത്വങ്ങളുടെ ഗുണനഫലം, Δx.ΔP<sub>x</sub>≥<math>\frac{h}{2 | + | ബലതന്ത്രത്തില്‍ ഒരു വസ്തുവിന്റെ അവസ്ഥയെ കുറിക്കുന്നതിന് (സ്ഥാനം, സംവേഗം), (ഊര്‍ജം, പ്രസ്തുത ഊര്‍ജാവസ്ഥയില്‍ സ്ഥിതിചെയ്യുന്ന സമയം) തുടങ്ങിയ ചര ജോഡികള്‍ പ്രധാനമാണ്. ഇവയെ വിഹിത ചരങ്ങള്‍ (canonical variables) എന്നു പറയും. സ്ഥൂലവസ്തുക്കളുടെ കാര്യത്തില്‍ വിഹിത ചരങ്ങളെ എത്ര കൃത്യതയോടെയും അളന്നു തിട്ടപ്പെടുത്താന്‍ കഴിയും. എന്നാല്‍ സൂക്ഷ്മകണങ്ങളുടെ കാര്യത്തില്‍ രണ്ടു ചരങ്ങളെയും ഒരേസമയം കൃത്യമായി നിര്‍ണയിക്കുക സാധ്യമല്ല എന്ന്അനിശ്ചിതത്വ തത്ത്വം അനുശാസിക്കുന്നു. ഉദാഹരണത്തിന്ഒരു കണത്തിന്റെ സ്ഥാനം 'x'-ഉം അതിന്റെ x ദിശയിലുള്ള സംവേഗം 'P<sub>x</sub>'-ഉം ആണെന്നിരിക്കട്ടെ. x അളക്കുന്നതില്‍ വരുന്ന പിശക് (error) 'Δx'-ഉം 'P<sub>x</sub>' അളക്കുന്നതില്‍ വരുന്ന പിശക് 'ΔP<sub>x</sub>'-ഉം ആണെങ്കില്‍ ഈ അനിശ്ചിതത്വങ്ങളുടെ ഗുണനഫലം, Δx.ΔP<sub>x</sub>≥<math>\frac{h}{2\pi}</math>എന്ന് അനിശ്ചിതത്വ തത്ത്വം പ്രസ്താവിക്കുന്നു. h-പ്ളാങ്ക് സ്ഥിരാങ്കം. Δx എത്രകണ്ട് കുറയുന്നുവോ (x എത്രമാത്രം സുനിശ്ചിതമാകുന്നുവോ) അത്രകണ്ട് Δp<sub>x></sub> കൂടുന്നു (P<sub>x</sub> അത്രയ്ക്ക് അനിശ്ചിതമാകുന്നു). |
| - | ഇതുപോലെ Δy.ΔP<sub>y</sub>≥h | + | ഇതുപോലെ Δy.ΔP<sub>y</sub>≥<math>\frac{h}{2\pi}</math>,Δz. |
| - | & | + | ΔP<sub>z</sub>≥<math>\frac{h}{2\pi}</math>എന്നീ പ്രസ്താവങ്ങളും ശരിയാണ്. ഒരു കണത്തിന്റെ ഊര്‍ജം 'E', സമയം 't' ഇവയെ ബന്ധിപ്പിക്കുന്ന അനിശ്ചിതത്വ നിയമമാണ് . |
| - | ΔE.Δt≥h | + | ΔE.Δt≥<math>\frac{h}{2\pi}</math> |
| - | സ്ഥൂലവസ്തുക്കള്‍ക്ക് പ്രസക്തമല്ലാത്ത ഈ നിയമം എന്തുകൊണ്ട് സൂക്ഷ്മകണങ്ങള്‍ക്കുമാത്രം ബാധകമാകുന്നു എന്ന് ഒരു ഉദാഹരണത്തിലൂടെ വ്യക്തമാക്കാം. ഒരു ഇലക്ട്രോണിന്റെ സ്ഥാനം 'x' കൃത്യമായി അളക്കുന്നതിനായി ഇലക്ട്രോണ്‍ ഉണ്ടാകാന്‍ സാധ്യതയുള്ള സ്ഥാനത്തേക്ക് & | + | സ്ഥൂലവസ്തുക്കള്‍ക്ക് പ്രസക്തമല്ലാത്ത ഈ നിയമം എന്തുകൊണ്ട് സൂക്ഷ്മകണങ്ങള്‍ക്കുമാത്രം ബാധകമാകുന്നു എന്ന് ഒരു ഉദാഹരണത്തിലൂടെ വ്യക്തമാക്കാം. ഒരു ഇലക്ട്രോണിന്റെ സ്ഥാനം 'x' കൃത്യമായി അളക്കുന്നതിനായി ഇലക്ട്രോണ്‍ ഉണ്ടാകാന്‍ സാധ്യതയുള്ള സ്ഥാനത്തേക്ക് λ തരംഗദൈര്‍ഘ്യമുള്ള ഒരു പ്രകാശ പുഞ്ജത്തെ അയയ്ക്കുമ്പോള്‍ ഒരു പ്രകാശകണം അതില്‍തട്ടി പ്രതിഫലിച്ചു വന്നാല്‍ സ്ഥാനനിര്‍ണയം ആയി. എന്നാല്‍, ഇലക്ട്രോണ്‍ λ ദൈര്‍ഘ്യത്തിനുള്ളില്‍ എവിടെയൊ ഉണ്ട് എന്ന അറിവേ അതു നല്‍കുന്നുള്ളു. അഥവാ,Δx ≈ λ ഇലക്ട്രോണിന്റെ സംവേഗം കാണണമെങ്കില്‍ രണ്ടുതവണ അതിന്റെ സ്ഥാനം കണ്ട് സ്ഥാനാന്തരത്തെ സമയംകൊണ്ട് ഹരിച്ച്പ്രവേഗംകണ്ട്,അതിനെപിണ്ഡംകൊണ്ട്ഗുണിക്കണം.എന്നാല്‍,ആദ്യത്തെസ്ഥാനനിര്‍ണയത്തില്‍ത്തന്നെ ഇലക്ട്രോണിന്റെ സംവേഗത്തില്‍ മാറ്റം വന്നിട്ടുണ്ടാകും. കാരണം, തരംഗദൈര്‍ഘ്യമുള്ള പ്രകാശ കണത്തിന് <math>\frac{h}{\lambda}</math>സംവേഗമുണ്ട്. ഇലക്ട്രോണില്‍ പതിച്ച പ്രകാശകണം അതിന്റെ സംവേഗത്തിലൊരു പങ്ക് (എത്രയെന്നറിയില്ല) ഇലക്ട്രോണിന് കൈമാറിയിരിക്കാം. അഥവാ, ഇലക്ട്രോണിന്റെസംവേഗത്തില്‍ഉണ്ടായഅനിശ്ചിതത്വംΔP<sub>x</sub>≈ |
| - | h/ | + | <math>\frac{h}{\lambda}</math> . അപ്പോള്‍ Δx.ΔP<sub>x</sub>≈Λ |
| - | .h/ | + | .<math>\frac{h}{\lambda}</math>≈ h എന്നു കിട്ടുന്നു. |
| - | Δxകുറയ്ക്കാന്& | + | Δxകുറയ്ക്കാന്λ കുറച്ചാല്‍ മതി; അഥവാ ആവൃത്തി കൂടിയ പ്രകാശം (ഉദാ. എക്സ്റേ) ഉപയോഗിച്ചാല്‍ മതി. അപ്പോള്‍ ΔP<sub>x</sub>≈<math>\frac{h}{\lambda}</math> വളരെക്കൂടും. അപ്പോഴും അനിശ്ചിതത്വങ്ങളുടെ ഗുണനഫലം 'h' ന്റെ തോതില്‍ തന്നെ ആയിരിക്കും. |
| - | മുന്‍ പറഞ്ഞത് ഒരു ഏകദേശ ചിത്രമാണ്. ഗണിതപരമായി Δx.ΔP<sub>x</sub>≥h | + | മുന്‍ പറഞ്ഞത് ഒരു ഏകദേശ ചിത്രമാണ്. ഗണിതപരമായി Δx.ΔP<sub>x</sub>≥<math>\frac{h}{2\pi}</math>എന്ന ബന്ധം നിഷ്പാദിപ്പിച്ചെടുക്കാന്‍ കഴിയും. |
ഇലക്ട്രോണിനുപകരം ഒരു സ്ഥൂലവസ്തുവാണ് പരിഗണിക്കുന്നതെങ്കില്‍ പ്രകാശകണം പതിച്ചാല്‍ അതിന്റെ സംവേഗത്തിലുണ്ടാകുന്ന മാറ്റം അവഗണനീയമായിരിക്കും. തന്മൂലം സ്ഥൂല വസ്തുക്കള്‍ക്ക് അനിശ്ചിതത്വ തത്ത്വം അപ്രസക്തമാണ്. | ഇലക്ട്രോണിനുപകരം ഒരു സ്ഥൂലവസ്തുവാണ് പരിഗണിക്കുന്നതെങ്കില്‍ പ്രകാശകണം പതിച്ചാല്‍ അതിന്റെ സംവേഗത്തിലുണ്ടാകുന്ന മാറ്റം അവഗണനീയമായിരിക്കും. തന്മൂലം സ്ഥൂല വസ്തുക്കള്‍ക്ക് അനിശ്ചിതത്വ തത്ത്വം അപ്രസക്തമാണ്. | ||
| - | അളവുപകരണത്തിന്റെയോ അളവ് രീതിയുടെയോ പരിമിതിയായി അനിശ്ചിതത്വ തത്ത്വത്തെ കണക്കാക്കരുത്. സൂക്ഷ്മകണങ്ങളുടെ ചലനത്തിന്റെ | + | അളവുപകരണത്തിന്റെയോ അളവ് രീതിയുടെയോ പരിമിതിയായി അനിശ്ചിതത്വ തത്ത്വത്തെ കണക്കാക്കരുത്. സൂക്ഷ്മകണങ്ങളുടെ ചലനത്തിന്റെ മൗലിക സ്വഭാവം തന്നെയാണത്. അതിനെ മറികടക്കുക സൈദ്ധാന്തികമായിത്തന്നെ സാധ്യമല്ല. |
| - | + | ക്ലാസിക്കല്‍ ഭൗതികശാസ്ത്രത്തിലെ കാരണതാ തത്ത്വത്തോട് (Causation principle) ഒട്ടും പൊരുത്തപ്പെടാത്ത ഒരു സ്ഥിതിവിശേഷമാണ് ഈ തത്ത്വത്തില്‍ അന്തര്‍ലീനമായിരിക്കുന്നത്. h എന്ന സ്ഥിരാങ്കത്തിന്റെ പരിമാണം അത്യധികം ചെറുതായത് കൊണ്ടാണ് ഈ സ്ഥിതിവിശേഷം ക്ളാസ്സിക്കല്‍ ഭൌതികശാസ്ത്രത്തില്‍ അനുഭവപ്പെടാതിരുന്നത്. നോ: ക്വാണ്ടം സിദ്ധാന്തം | |
(പ്രൊഫ. ടി.ബി. തോമസ്, സ.പ.) | (പ്രൊഫ. ടി.ബി. തോമസ്, സ.പ.) | ||
| + | [[Category:ഭൗതികം-ക്വാണ്ടം ബലതന്ത്രം]] | ||
Current revision as of 10:53, 24 നവംബര്‍ 2014
അനിശ്ചിതത്വ തത്ത്വം
Uncertainty principle
മൗലിക പ്രാധാന്യമുള്ള ഒരു ഭൌതികശാസ്ത്ര തത്ത്വം. 1927-ല്‍, ജര്‍മന്‍ ഭൌതികശാസ്ത്രജ്ഞനായ വെര്‍ണര്‍ ഹൈസന്‍ബര്‍ഗ് ആണ് ഈ തത്ത്വം അവതരിപ്പിച്ചത്. ഇതു സൂക്ഷ്മകണങ്ങളുടെ ക്വാണ്ടം സ്വഭാവത്തിന്റെ ഒരു പരിണതഫലമാണ്.
ബലതന്ത്രത്തില്‍ ഒരു വസ്തുവിന്റെ അവസ്ഥയെ കുറിക്കുന്നതിന് (സ്ഥാനം, സംവേഗം), (ഊര്‍ജം, പ്രസ്തുത ഊര്‍ജാവസ്ഥയില്‍ സ്ഥിതിചെയ്യുന്ന സമയം) തുടങ്ങിയ ചര ജോഡികള്‍ പ്രധാനമാണ്. ഇവയെ വിഹിത ചരങ്ങള്‍ (canonical variables) എന്നു പറയും. സ്ഥൂലവസ്തുക്കളുടെ കാര്യത്തില്‍ വിഹിത ചരങ്ങളെ എത്ര കൃത്യതയോടെയും അളന്നു തിട്ടപ്പെടുത്താന്‍ കഴിയും. എന്നാല്‍ സൂക്ഷ്മകണങ്ങളുടെ കാര്യത്തില്‍ രണ്ടു ചരങ്ങളെയും ഒരേസമയം കൃത്യമായി നിര്‍ണയിക്കുക സാധ്യമല്ല എന്ന്അനിശ്ചിതത്വ തത്ത്വം അനുശാസിക്കുന്നു. ഉദാഹരണത്തിന്ഒരു കണത്തിന്റെ സ്ഥാനം 'x'-ഉം അതിന്റെ x ദിശയിലുള്ള സംവേഗം 'Px'-ഉം ആണെന്നിരിക്കട്ടെ. x അളക്കുന്നതില്‍ വരുന്ന പിശക് (error) 'Δx'-ഉം 'Px' അളക്കുന്നതില്‍ വരുന്ന പിശക് 'ΔPx'-ഉം ആണെങ്കില്‍ ഈ അനിശ്ചിതത്വങ്ങളുടെ ഗുണനഫലം, Δx.ΔPx≥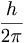
എന്ന് അനിശ്ചിതത്വ തത്ത്വം പ്രസ്താവിക്കുന്നു. h-പ്ളാങ്ക് സ്ഥിരാങ്കം. Δx എത്രകണ്ട് കുറയുന്നുവോ (x എത്രമാത്രം സുനിശ്ചിതമാകുന്നുവോ) അത്രകണ്ട് Δpx> കൂടുന്നു (Px അത്രയ്ക്ക് അനിശ്ചിതമാകുന്നു).
ഇതുപോലെ Δy.ΔPy≥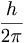,Δz.
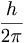ΔPz≥എന്നീ പ്രസ്താവങ്ങളും ശരിയാണ്. ഒരു കണത്തിന്റെ ഊര്‍ജം 'E', സമയം 't' ഇവയെ ബന്ധിപ്പിക്കുന്ന അനിശ്ചിതത്വ നിയമമാണ് .
ΔE.Δt≥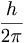
സ്ഥൂലവസ്തുക്കള്‍ക്ക് പ്രസക്തമല്ലാത്ത ഈ നിയമം എന്തുകൊണ്ട് സൂക്ഷ്മകണങ്ങള്‍ക്കുമാത്രം ബാധകമാകുന്നു എന്ന് ഒരു ഉദാഹരണത്തിലൂടെ വ്യക്തമാക്കാം. ഒരു ഇലക്ട്രോണിന്റെ സ്ഥാനം 'x' കൃത്യമായി അളക്കുന്നതിനായി ഇലക്ട്രോണ്‍ ഉണ്ടാകാന്‍ സാധ്യതയുള്ള സ്ഥാനത്തേക്ക് λ തരംഗദൈര്‍ഘ്യമുള്ള ഒരു പ്രകാശ പുഞ്ജത്തെ അയയ്ക്കുമ്പോള്‍ ഒരു പ്രകാശകണം അതില്‍തട്ടി പ്രതിഫലിച്ചു വന്നാല്‍ സ്ഥാനനിര്‍ണയം ആയി. എന്നാല്‍, ഇലക്ട്രോണ്‍ λ ദൈര്‍ഘ്യത്തിനുള്ളില്‍ എവിടെയൊ ഉണ്ട് എന്ന അറിവേ അതു നല്‍കുന്നുള്ളു. അഥവാ,Δx ≈ λ ഇലക്ട്രോണിന്റെ സംവേഗം കാണണമെങ്കില്‍ രണ്ടുതവണ അതിന്റെ സ്ഥാനം കണ്ട് സ്ഥാനാന്തരത്തെ സമയംകൊണ്ട് ഹരിച്ച്പ്രവേഗംകണ്ട്,അതിനെപിണ്ഡംകൊണ്ട്ഗുണിക്കണം.എന്നാല്‍,ആദ്യത്തെസ്ഥാനനിര്‍ണയത്തില്‍ത്തന്നെ ഇലക്ട്രോണിന്റെ സംവേഗത്തില്‍ മാറ്റം വന്നിട്ടുണ്ടാകും. കാരണം, തരംഗദൈര്‍ഘ്യമുള്ള പ്രകാശ കണത്തിന്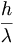 
സംവേഗമുണ്ട്. ഇലക്ട്രോണില്‍ പതിച്ച പ്രകാശകണം അതിന്റെ സംവേഗത്തിലൊരു പങ്ക് (എത്രയെന്നറിയില്ല) ഇലക്ട്രോണിന് കൈമാറിയിരിക്കാം. അഥവാ, ഇലക്ട്രോണിന്റെസംവേഗത്തില്‍ഉണ്ടായഅനിശ്ചിതത്വംΔPx≈
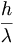. അപ്പോള്‍ Δx.ΔPx≈Λ
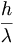.≈ h എന്നു കിട്ടുന്നു.
Δxകുറയ്ക്കാന്λ കുറച്ചാല്‍ മതി; അഥവാ ആവൃത്തി കൂടിയ പ്രകാശം (ഉദാ. എക്സ്റേ) ഉപയോഗിച്ചാല്‍ മതി. അപ്പോള്‍ ΔPx≈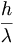 വളരെക്കൂടും. അപ്പോഴും അനിശ്ചിതത്വങ്ങളുടെ ഗുണനഫലം 'h' ന്റെ തോതില്‍ തന്നെ ആയിരിക്കും.
മുന്‍ പറഞ്ഞത് ഒരു ഏകദേശ ചിത്രമാണ്. ഗണിതപരമായി Δx.ΔPx≥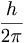എന്ന ബന്ധം നിഷ്പാദിപ്പിച്ചെടുക്കാന്‍ കഴിയും.
ഇലക്ട്രോണിനുപകരം ഒരു സ്ഥൂലവസ്തുവാണ് പരിഗണിക്കുന്നതെങ്കില്‍ പ്രകാശകണം പതിച്ചാല്‍ അതിന്റെ സംവേഗത്തിലുണ്ടാകുന്ന മാറ്റം അവഗണനീയമായിരിക്കും. തന്മൂലം സ്ഥൂല വസ്തുക്കള്‍ക്ക് അനിശ്ചിതത്വ തത്ത്വം അപ്രസക്തമാണ്.
അളവുപകരണത്തിന്റെയോ അളവ് രീതിയുടെയോ പരിമിതിയായി അനിശ്ചിതത്വ തത്ത്വത്തെ കണക്കാക്കരുത്. സൂക്ഷ്മകണങ്ങളുടെ ചലനത്തിന്റെ മൗലിക സ്വഭാവം തന്നെയാണത്. അതിനെ മറികടക്കുക സൈദ്ധാന്തികമായിത്തന്നെ സാധ്യമല്ല.
ക്ലാസിക്കല്‍ ഭൗതികശാസ്ത്രത്തിലെ കാരണതാ തത്ത്വത്തോട് (Causation principle) ഒട്ടും പൊരുത്തപ്പെടാത്ത ഒരു സ്ഥിതിവിശേഷമാണ് ഈ തത്ത്വത്തില്‍ അന്തര്‍ലീനമായിരിക്കുന്നത്. h എന്ന സ്ഥിരാങ്കത്തിന്റെ പരിമാണം അത്യധികം ചെറുതായത് കൊണ്ടാണ് ഈ സ്ഥിതിവിശേഷം ക്ളാസ്സിക്കല്‍ ഭൌതികശാസ്ത്രത്തില്‍ അനുഭവപ്പെടാതിരുന്നത്. നോ: ക്വാണ്ടം സിദ്ധാന്തം
(പ്രൊഫ. ടി.ബി. തോമസ്, സ.പ.)
