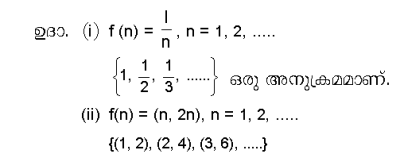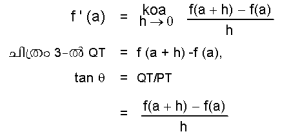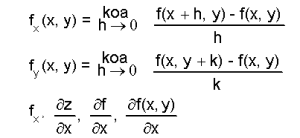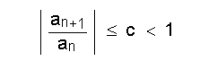This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
അനാലിസിസ് (ഗണിതം)
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→മിതീയ ഗണങ്ങള്) |
Mksol (സംവാദം | സംഭാവനകള്) (→അഭികേന്ദ്രസരണവും അപകേന്ദ്രസരണവും) |
||
| (ഇടക്കുള്ള 55 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 8: | വരി 8: | ||
==ചരിത്രം== | ==ചരിത്രം== | ||
| - | ഗണിതശാസ്ത്രത്തില് പ്രാചീനകാലത്തു ഗ്രീസിലും ഇന്ത്യയിലുമുണ്ടായിട്ടുള്ള ജ്യാമിതീയവും ബീജഗണിതപരവുമായ വളര്ച്ച അനാലിസിസിന്റെ അന്തര്ധാരകളായിരിക്കാമെങ്കിലും എ.ഡി. 1600 മുതലാണ് ഇതു ശ്രദ്ധാര്ഹമായ ഒരു ശാസ്ത്രശാഖയായിത്തീര്ന്നത്. ബലതന്ത്ര (Mechanics)ത്തിന്റെയും താത്ത്വികഭൌതിക (Theoretical Physics)ത്തിന്റെയും അവശ്യ വളര്ച്ചയ്ക്കാധാരമായിട്ടാണ് ഈ ശാഖയുണ്ടായത്. അവകലനവും സമാകലനവും (Diiferentiation and integration), സാധാരണ അവകലസമവാക്യങ്ങളും വ്യതിയാനകലനവും (Ordinary Differential equations and Different Calculus) ബലതന്ത്രത്തിനുവേണ്ടിയാണുണ്ടായത്. ധ്വാനിക (Acoustics)ത്തില് നിന്നും താപഗതിക (Thermodynamics)ത്തില് നിന്നും ഫൂറിയേ ശ്രേണി(Fourier series)യും പ്രകാശിക(Optics)ത്തില്നിന്ന് സമ്മിശ്ര വിശ്ളേഷണവും (Complex Analysis), ഇലാസ്തികത (Elasticity), ദ്രവഗതികം (Hydrodynamics), വിദ്യുത്ഗതികം (Electrodynamics) എന്നിവയില് നിന്ന് ആംശിക-അവകലവാക്യങ്ങളും (Partial Diiferential equations) പ്രേരിതമായെന്നു സാമാന്യമായി പറയാം. 19-ാം ശ.-ത്തില് ബലതന്ത്രം, താപഗതികം എന്നിവയിലെ സാംഖ്യികദര്ശനങ്ങളില്നിന്നാണ് സാംഖ്യികസംഭാവ്യത (Statistical probability) പോലും ഉണ്ടായതെന്നവാദം നിലവിലുണ്ട്. ശാസ്ത്രജ്ഞന്മാരായ | + | ഗണിതശാസ്ത്രത്തില് പ്രാചീനകാലത്തു ഗ്രീസിലും ഇന്ത്യയിലുമുണ്ടായിട്ടുള്ള ജ്യാമിതീയവും ബീജഗണിതപരവുമായ വളര്ച്ച അനാലിസിസിന്റെ അന്തര്ധാരകളായിരിക്കാമെങ്കിലും എ.ഡി. 1600 മുതലാണ് ഇതു ശ്രദ്ധാര്ഹമായ ഒരു ശാസ്ത്രശാഖയായിത്തീര്ന്നത്. ബലതന്ത്ര (Mechanics)ത്തിന്റെയും താത്ത്വികഭൌതിക (Theoretical Physics)ത്തിന്റെയും അവശ്യ വളര്ച്ചയ്ക്കാധാരമായിട്ടാണ് ഈ ശാഖയുണ്ടായത്. അവകലനവും സമാകലനവും (Diiferentiation and integration), സാധാരണ അവകലസമവാക്യങ്ങളും വ്യതിയാനകലനവും (Ordinary Differential equations and Different Calculus) ബലതന്ത്രത്തിനുവേണ്ടിയാണുണ്ടായത്. ധ്വാനിക (Acoustics)ത്തില് നിന്നും താപഗതിക (Thermodynamics)ത്തില് നിന്നും ഫൂറിയേ ശ്രേണി(Fourier series)യും പ്രകാശിക(Optics)ത്തില്നിന്ന് സമ്മിശ്ര വിശ്ളേഷണവും (Complex Analysis), ഇലാസ്തികത (Elasticity), ദ്രവഗതികം (Hydrodynamics), വിദ്യുത്ഗതികം (Electrodynamics) എന്നിവയില് നിന്ന് ആംശിക-അവകലവാക്യങ്ങളും (Partial Diiferential equations) പ്രേരിതമായെന്നു സാമാന്യമായി പറയാം. 19-ാം ശ.-ത്തില് ബലതന്ത്രം, താപഗതികം എന്നിവയിലെ സാംഖ്യികദര്ശനങ്ങളില്നിന്നാണ് സാംഖ്യികസംഭാവ്യത (Statistical probability) പോലും ഉണ്ടായതെന്നവാദം നിലവിലുണ്ട്. ശാസ്ത്രജ്ഞന്മാരായ ഐസക് ന്യൂട്ടനും (1642-1727) ഗോട്ഫ്രീഡ് ലൈബ്നിറ്റ്സും (1646-1716) കലന(Calculus)ത്തിന്റെ നിശ്ചിതമായ മാര്ഗങ്ങള് കണ്ടെത്തിയതോടെയാണ് അനാലിസിസ് സര്വശാസ്ത്രവ്യാപിയായ ഒരു വിജ്ഞാനശാഖയായിത്തീര്ന്നത്. |
== സ്വഭാവം== | == സ്വഭാവം== | ||
| - | അവകലനവും സമാകലനവും അനാലിസിസിലെ അടിസ്ഥാനമാര്ഗങ്ങളാണെങ്കിലും അനന്തത ( | + | അവകലനവും സമാകലനവും അനാലിസിസിലെ അടിസ്ഥാനമാര്ഗങ്ങളാണെങ്കിലും അനന്തത (Infinity) ആണ് അടിസ്ഥാനതത്ത്വം. വാസ്തവത്തില് ഗണിതശാസ്ത്രം തന്നെ അനന്തതകളുടെ പഠനമാണെന്നു പറയാം. പരിമിതമായ കാര്യങ്ങള് മിക്കവയും പ്രാഥമികഗണിതത്തില് കഴിഞ്ഞാല് അവശേഷിക്കുന്ന തൊണ്ണൂറു ശ.മാ.വും അനന്തത ഉള്ക്കൊള്ളുന്ന പഠനങ്ങളാണ്. അനന്തമായ വലുപ്പം, അനന്തസൂക്ഷ്മം, അനന്തസാമീപ്യം, അനന്തമായ ഉപവിഭജനം എന്നിവയും അനന്ത-അനുക്രമം, അനന്തശ്രേണി, ഫലനം, ഫലനത്തിന്റെ അവിച്ഛിന്നത, ഫലനത്തിന്റെ വ്യുത്പന്നം (derivative), ഫലനത്തിന്റെ സമാകലം (Integral) എന്നിവയുമാണ് വിശ്ളേഷണത്തില് സ്പര്ശിക്കപ്പെടുന്ന കാര്യങ്ങള്. അവകലജഗുണാങ്കം (differential) ഗണിത തത്ത്വങ്ങളിലെന്നല്ല, സാമ്പത്തികശാസ്ത്രം പോലുള്ള എല്ലാ വിജ്ഞാനശാഖകളിലും മൌലികപ്രാധാന്യമര്ഹിക്കുന്ന ആശയമാണ്. |
=== വാസ്തവിക സംഖ്യകള് === | === വാസ്തവിക സംഖ്യകള് === | ||
| വരി 19: | വരി 19: | ||
| - | ബി.സി. 5-ഉം 4-ഉം ശ.-ങ്ങളില് ഗ്രീക്കുകാര് അനാലിസിസിലെ അതിപ്രധാനമായ ചില പ്രശ്നങ്ങള്ക്കു പരിഹാരം നല്കി. | + | ബി.സി. 5-ഉം 4-ഉം ശ.-ങ്ങളില് ഗ്രീക്കുകാര് അനാലിസിസിലെ അതിപ്രധാനമായ ചില പ്രശ്നങ്ങള്ക്കു പരിഹാരം നല്കി. √2 ഒരു വിഗണസംഖ്യയാണ് (irrational number: അനാനുപാതികസംഖ്യ). ഗ്രീസിലും ഇന്ത്യയിലും π = 3.14159.... എന്ന വിഗണസംഖ്യയെക്കുറിച്ചുള്ള പഠനങ്ങളുണ്ടായി. വ്യാസാര്ധം 1 ആയിട്ടുള്ള വൃത്തത്തിന്റെ വിസ്തീര്ണം ആണ് π വൃത്തത്തിനു തുല്യവ്യാപ്തിയുള്ള ചതുരം നിര്മിക്കുന്ന പ്രശ്നത്തിനു പ്രാചീനകാലത്തുതന്നെ ഉത്തരം കണ്ടെത്താന് പരിശ്രമം ആരംഭിച്ചിരുന്നു. ഈ വഴിക്കുള്ള പരിശ്രമങ്ങളെല്ലാം 17-ാം ശ.-ത്തിലെ സമാകലസിദ്ധാന്തത്തിനും കലനത്തിന്റെ താത്വികവളര്ച്ചയ്ക്കും കാരണമായി. |
| വരി 28: | വരി 28: | ||
order | order | ||
| - | വാസ്തവിക സംഖ്യകളെ സംബന്ധിച്ച ഒരാശയമാണ് ക്രമം. ഗണങ്ങളെയും 'ക്രമ'പ്പെടുത്താന് കഴിയും. 8-നെക്കാള് ചെറുതാണ് 3 എന്നത് 3 < 8 എന്നും 3 നെക്കാള് വലുതാണ് 8 എന്നത് 8 > 3 എന്നും സൂചിപ്പിക്കപ്പെടുന്നു. സമതയും കൂടി ഉള്പ്പെടുത്തുമ്പോള് ≤,≥ എന്നീ പ്രതീകങ്ങളാണ് ഉപയോഗിക്കുന്നത്. ഉദാ. a& | + | വാസ്തവിക സംഖ്യകളെ സംബന്ധിച്ച ഒരാശയമാണ് ക്രമം. ഗണങ്ങളെയും 'ക്രമ'പ്പെടുത്താന് കഴിയും. 8-നെക്കാള് ചെറുതാണ് 3 എന്നത് 3 < 8 എന്നും 3 നെക്കാള് വലുതാണ് 8 എന്നത് 8 > 3 എന്നും സൂചിപ്പിക്കപ്പെടുന്നു. സമതയും കൂടി ഉള്പ്പെടുത്തുമ്പോള് ≤, ≥ എന്നീ പ്രതീകങ്ങളാണ് ഉപയോഗിക്കുന്നത്. ഉദാ. a≤b; c≥d; ഇതില് a,b, c, d എന്നിവ വാസ്തവിക സംഖ്യകളാണ്. |
=== നിരപേക്ഷമൂല്യം === | === നിരപേക്ഷമൂല്യം === | ||
Absolute value | Absolute value | ||
| - | + | [[Image:p500.png]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
== പൂര്ണത== | == പൂര്ണത== | ||
| - | + | Completeness | |
വാസ്തവിക സംഖ്യാഗണത്തെ ആധാരമാക്കിയാണ് ഇതില് ആശയങ്ങള് പ്രതിപാദിക്കുന്നത്. ഒരു വാസ്തവിക സംഖ്യാഗണ(S)ത്തിലുള്ള ഏത് അംഗത്തിനെക്കാളും വലിയതായി ഒരു വാസ്തവിക സംഖ്യ (b) സ്വീകരിക്കാനുണ്ടെങ്കില്, ആ സംഖ്യ b ആണ്, s ഗണത്തിന്റെ ഒരു b എന്ന ഒരു ഉന്നത പരിബന്ധം (upper bound); S-ലെ ഒരംഗമാകണമെന്നില്ല. ഉദാ. S ={1/8,1/4,1/2}എന്ന ഗണത്തിലെ ഏതു സംഖ്യയും 1-നെക്കാള് ചെറുതാണ്. അതുകൊണ്ട് ട-ന്റെ ഒരു ഉന്നതപരിബന്ധമാണ് 1. S ഗണത്തിനുണ്ടാകാവുന്ന അനവധി പരിബന്ധങ്ങളില്വച്ച് ഏറ്റവും ചെറുതിനെയാണ് അല്പതമ-ഉന്നതപരിബന്ധം (least upper bound:lub ) അഥവാ സുപ്രീമം (Supremum:sup) എന്നു പറയുന്നത്. അതുപോലെ ഏത് അംഗത്തെക്കാളും ചെറുതായ ഒരു വാസ്തവികസംഖ്യയുണ്ടെങ്കില് അതിനെ ഒരു നിമ്നപരിബന്ധം (lower bound) എന്നും അത്തരം പരിബന്ധങ്ങളില് ഏറ്റവും വലിയതിനെ അധികതമ നിമ്നപരിബന്ധം (greatest lower bound:glb) അഥവാ ഇന്ഫിമം (infimum: inf) എന്നും പറയുന്നു. | വാസ്തവിക സംഖ്യാഗണത്തെ ആധാരമാക്കിയാണ് ഇതില് ആശയങ്ങള് പ്രതിപാദിക്കുന്നത്. ഒരു വാസ്തവിക സംഖ്യാഗണ(S)ത്തിലുള്ള ഏത് അംഗത്തിനെക്കാളും വലിയതായി ഒരു വാസ്തവിക സംഖ്യ (b) സ്വീകരിക്കാനുണ്ടെങ്കില്, ആ സംഖ്യ b ആണ്, s ഗണത്തിന്റെ ഒരു b എന്ന ഒരു ഉന്നത പരിബന്ധം (upper bound); S-ലെ ഒരംഗമാകണമെന്നില്ല. ഉദാ. S ={1/8,1/4,1/2}എന്ന ഗണത്തിലെ ഏതു സംഖ്യയും 1-നെക്കാള് ചെറുതാണ്. അതുകൊണ്ട് ട-ന്റെ ഒരു ഉന്നതപരിബന്ധമാണ് 1. S ഗണത്തിനുണ്ടാകാവുന്ന അനവധി പരിബന്ധങ്ങളില്വച്ച് ഏറ്റവും ചെറുതിനെയാണ് അല്പതമ-ഉന്നതപരിബന്ധം (least upper bound:lub ) അഥവാ സുപ്രീമം (Supremum:sup) എന്നു പറയുന്നത്. അതുപോലെ ഏത് അംഗത്തെക്കാളും ചെറുതായ ഒരു വാസ്തവികസംഖ്യയുണ്ടെങ്കില് അതിനെ ഒരു നിമ്നപരിബന്ധം (lower bound) എന്നും അത്തരം പരിബന്ധങ്ങളില് ഏറ്റവും വലിയതിനെ അധികതമ നിമ്നപരിബന്ധം (greatest lower bound:glb) അഥവാ ഇന്ഫിമം (infimum: inf) എന്നും പറയുന്നു. | ||
| വരി 70: | വരി 56: | ||
A , B ഇവ ശൂന്യമല്ലാത്ത രണ്ടു വാസ്തവിക സംഖ്യാഗണങ്ങളും f : A → B ഒരു ഫലനവും ആണെന്നു കരുതുക. x<sub>1</sub>, x<sub>2</sub> ഇവ A-യിലെ അംഗങ്ങളും x<sub>1</sub> < x<sub>2</sub> ഉം ആകുമ്പോഴെല്ലാം f(x<sub>1</sub>) ≤ f(x<sub>2</sub>) ആണെങ്കില് f വര്ധമാനഫലനം ആണ് എന്നു പറയുന്നു. , x<sub>1</sub>, x<sub>2</sub> ആകുമ്പോഴെല്ലാം f(x<sub>1</sub>) | A , B ഇവ ശൂന്യമല്ലാത്ത രണ്ടു വാസ്തവിക സംഖ്യാഗണങ്ങളും f : A → B ഒരു ഫലനവും ആണെന്നു കരുതുക. x<sub>1</sub>, x<sub>2</sub> ഇവ A-യിലെ അംഗങ്ങളും x<sub>1</sub> < x<sub>2</sub> ഉം ആകുമ്പോഴെല്ലാം f(x<sub>1</sub>) ≤ f(x<sub>2</sub>) ആണെങ്കില് f വര്ധമാനഫലനം ആണ് എന്നു പറയുന്നു. , x<sub>1</sub>, x<sub>2</sub> ആകുമ്പോഴെല്ലാം f(x<sub>1</sub>) | ||
| - | ≥ f(x<sub>2</sub>) ആണെങ്കില് f ഹ്രസ്വമാനഫലനം ആണെന്നും പറയുന്നു. | + | ≥ f(x<sub>2</sub>) ആണെങ്കില് f ഹ്രസ്വമാനഫലനം ആണെന്നും പറയുന്നു. A എന്ന ഗണത്തില് f എന്ന ഫലനം വര്ധമാനമോ അഥവാ ഹ്രസ്വമാനമോ ആണെങ്കില് f ഏകദിഷ്ടമാണ് എന്നു പറയുന്നു. |
== മിതീയ ഗണങ്ങള് == | == മിതീയ ഗണങ്ങള് == | ||
| വരി 78: | വരി 64: | ||
=== ദൂരഫലനം അഥവാ മെട്രിക്'=== | === ദൂരഫലനം അഥവാ മെട്രിക്'=== | ||
| - | a, b എന്നിവ A എന്ന ഗണത്തിലെ രണ്ടംഗങ്ങളാണെന്നു കരുതുക. d(a, b) എന്ന ചിഹ്നം കൊണ്ടു സൂചിപ്പിക്കപ്പെടുന്നതും a, b എന്നിവയുമായി ബന്ധപ്പെടുത്താവുന്നതുമായ ഒരു വാസ്തവികസംഖ്യ താഴെ ചേര്ക്കുന്ന വ്യവസ്ഥകള്ക്കു വിധേയമാണെങ്കില് d ഒരു മെട്രിക് അഥവാ ദൂരഫലനമാണെന്നു പറയുന്നു; (i) d (a, b) അന്യൂന സംഖ്യയാണ്; അതായത് d(a, b) ≥o.(ii) a-ഉം b-ഉം തുല്യമാണെങ്കില് മാത്രമേ, d(a, b)യുടെ മൂല്യം പൂജ്യം ആകുന്നുള്ളു. (iii) d(a,b)ഉം d( | + | a, b എന്നിവ A എന്ന ഗണത്തിലെ രണ്ടംഗങ്ങളാണെന്നു കരുതുക. d(a, b) എന്ന ചിഹ്നം കൊണ്ടു സൂചിപ്പിക്കപ്പെടുന്നതും a, b എന്നിവയുമായി ബന്ധപ്പെടുത്താവുന്നതുമായ ഒരു വാസ്തവികസംഖ്യ താഴെ ചേര്ക്കുന്ന വ്യവസ്ഥകള്ക്കു വിധേയമാണെങ്കില് d ഒരു മെട്രിക് അഥവാ ദൂരഫലനമാണെന്നു പറയുന്നു; (i) d (a, b) അന്യൂന സംഖ്യയാണ്; അതായത് d(a, b) ≥o.(ii) a-ഉം b-ഉം തുല്യമാണെങ്കില് മാത്രമേ, d(a, b)യുടെ മൂല്യം പൂജ്യം ആകുന്നുള്ളു. (iii) d(a,b)ഉം d(b, a)ഉം തുല്യമാണ്. (iv) a, b, c എന്നിവ A ഗണത്തിലുള്ള അംഗങ്ങളാണെങ്കില്, d(a, b) + d(b, c) ≥ d(a, c). ഇതിനെ ത്രികോണ-അസമത എന്നു പറയുന്നു. |
മിതീയഗണം എന്നതുകൊണ്ടുദ്ദേശിക്കുന്നത്, ഒരു ഗണവും (A) അതിനെ ആശ്രയിച്ചിരിക്കുന്ന ഒരു മെട്രിക്കും (d) ചേര്ന്ന ജോടി (A,d) ആണ്. ഇതിന് A എന്നു മാത്രമായിട്ടും പ്രതീകം ഉപയോഗിക്കാറുണ്ട്. | മിതീയഗണം എന്നതുകൊണ്ടുദ്ദേശിക്കുന്നത്, ഒരു ഗണവും (A) അതിനെ ആശ്രയിച്ചിരിക്കുന്ന ഒരു മെട്രിക്കും (d) ചേര്ന്ന ജോടി (A,d) ആണ്. ഇതിന് A എന്നു മാത്രമായിട്ടും പ്രതീകം ഉപയോഗിക്കാറുണ്ട്. | ||
| - | ഉദാ. A {x:x വാസ്തവികസംഖ്യ} A-യിലുള്ള ഏതു അംഗജോടികള് (x<sub>1</sub>,x<sub>2</sub>)ക്കും യോജിക്കുന്നവിധം d-യെ നിര്വചിക്കാം. d (x<sub>1</sub>,x<sub>2</sub>) = | | + | ഉദാ. A {x:x വാസ്തവികസംഖ്യ} A-യിലുള്ള ഏതു അംഗജോടികള് (x<sub>1</sub>,x<sub>2</sub>)ക്കും യോജിക്കുന്നവിധം d-യെ നിര്വചിക്കാം. d (x<sub>1</sub>,x<sub>2</sub>) = |x<sub>1</sub>-x<sub>2</sub>| ഒരു മെട്രിക് ആണ്. |
=== സാമീപ്യങ്ങള് === | === സാമീപ്യങ്ങള് === | ||
Neighbourhoods | Neighbourhoods | ||
| - | + | [[Image:p.no.474.jpg|thumb|200x150px|right|ചിത്രം 1]] | |
| - | (A, d) മിതീയഗണമാണെന്നിരിക്കട്ടെ. A-യിലെ ഒരുസ്ഥിരബിന്ദുവും ε ഒരു ധനവാസ്തവിക സംഖ്യയുമാണെന്നു കരുതുക. ഈ വ്യവസ്ഥിതിയില് d(a,x)-ന്റെ മൂല്യം ε-നെക്കാള് ചെറുതായിരിക്കുന്ന വിധത്തിലുള്ള A-യിലെ x അംഗങ്ങള് ചേര്ന്ന ഗണത്തെ a-യുടെ ഒരു സാമീപ്യം എന്നു പറയുന്നു; N(a, ε) എന്നാണിതിന്റെ പ്രതീകം. അതായത് N (a, ε) = {x:x& | + | (A, d) മിതീയഗണമാണെന്നിരിക്കട്ടെ. A-യിലെ ഒരുസ്ഥിരബിന്ദുവും ε ഒരു ധനവാസ്തവിക സംഖ്യയുമാണെന്നു കരുതുക. ഈ വ്യവസ്ഥിതിയില് d(a,x)-ന്റെ മൂല്യം ε-നെക്കാള് ചെറുതായിരിക്കുന്ന വിധത്തിലുള്ള A-യിലെ x അംഗങ്ങള് ചേര്ന്ന ഗണത്തെ a-യുടെ ഒരു സാമീപ്യം എന്നു പറയുന്നു; N(a, ε) എന്നാണിതിന്റെ പ്രതീകം. അതായത് N (a, ε) = {x : x ε A, d (a, x)< ε}. ഈ ഗണത്തില്നിന്ന് a എന്ന ബിന്ദു ഒഴിവാക്കിയാല്, അവശേഷിക്കുന്നത്, N' (a, ε) അപവര്ജിതസാമീപ്യം (deleted neighbourhood) ആണ്. |
== ആന്തരബിന്ദുക്കളും അതിര്ത്തിബിന്ദുക്കളും == | == ആന്തരബിന്ദുക്കളും അതിര്ത്തിബിന്ദുക്കളും == | ||
| വരി 94: | വരി 80: | ||
(Interior points and boundary points). | (Interior points and boundary points). | ||
| - | + | M എന്ന ഗണത്തിന്റെ ഉപഗണമാണ് A എന്നു കരുതുക. ഒരു ഗണ(A)ത്തിലെ അംഗം 'a' ആ ഗണത്തിന്റെ ഒരു 'ആന്തരബിന്ദു'വാകുന്നത്, അതിന്റെ ഏതെങ്കിലും ഒരു സാമീപ്യം N (a, ε) മുഴുവനും അ-ല് ഉള്ക്കൊള്ളുമ്പോഴാണ്; സാമീപ്യം ഒന്നും A-യില് ഉള്ക്കൊള്ളുന്നില്ലെങ്കില് ആ അംഗം 'a' A-യുടെ ഒരു ബഹിര്ബിന്ദു (exterior point) വും ആകും; ഓരോ സാമീപ്യ N(a, ε) വും A യിലെയും A-യ്ക്കു പുറത്തുള്ള ഭാഗത്തെയും അതായത്, M-A യേയും സന്ധിക്കുന്നു (Intersect) എങ്കില് A-യുടെ ഒരു അതിര്ബിന്ദുവാണ് a എന്നു പറയുന്നു. ആന്തരബിന്ദു സമൂഹത്തിന് ആ ഗണത്തിന്റെ ആന്തരഭാഗം (interior) എന്നും ബാഹ്യബിന്ദുക്കളുടെ സമൂഹത്തിന് ആ ഗണത്തിന്റെ ബഹിര്ഭാഗം (exterior) എന്നും പറയുന്നു; അതിര്ബിന്ദുക്കളുടെ സമൂഹം ആ ഗണത്തിന്റെ അതിര്ത്തിഭാഗ(boundary)വും. | |
അതിര്ത്തിഭാഗവുംകൂടി ഉള്പ്പെടുന്ന ഗണത്തെ സംവൃതഗണം (closed set) എന്നും ആന്തരഭാഗം ഉള്പ്പെടുന്ന ഗണത്തെ വിവൃതഗണം (open set) എന്നും പറയുന്നു. | അതിര്ത്തിഭാഗവുംകൂടി ഉള്പ്പെടുന്ന ഗണത്തെ സംവൃതഗണം (closed set) എന്നും ആന്തരഭാഗം ഉള്പ്പെടുന്ന ഗണത്തെ വിവൃതഗണം (open set) എന്നും പറയുന്നു. | ||
| വരി 104: | വരി 90: | ||
Sequences | Sequences | ||
| - | അനുക്രമം നിര്വചിക്കപ്പെടുന്നത് ഒരു ഫലനമായിട്ടാണ്. f : N | + | അനുക്രമം നിര്വചിക്കപ്പെടുന്നത് ഒരു ഫലനമായിട്ടാണ്. f : N → M അതായത്, നിസര്ഗസംഖ്യകളെ M എന്ന ഗണത്തിലെ അംഗങ്ങളുമായി ബന്ധപ്പെടുത്തുന്ന ഫലനമാണ് M-ലെ ഒരു അനുക്രമം. |
| - | + | [[Image:p501.png]] | |
| + | === അനുക്രമസീമ === | ||
| - | {1,1/2,1/3,.........} | + | 'ബിന്ദുക്കള്' ക്രമമായിരിക്കുമ്പോള് ആ അനുക്രമത്തിന്റെ പ്രവണത നിര്ണയിക്കുന്നതിനുള്ള ആശയമാണ് സീമ. ഒരു സ്ഥിരബിന്ദുവാണ് സീമയെന്നു പറയാം. സാങ്കേതികമായി പറഞ്ഞാല് പരിമേയമായ ഏതാനും അംഗങ്ങളൊഴിച്ച് ശേഷിക്കുന്ന മറ്റു സാന്തമോ അനന്തമോ അംഗങ്ങള് മുഴുവനും ഉള്പ്പെടുന്നതായ ഒരു സാമീപ്യം b എന്ന ഒരു ബിന്ദുവിനുണ്ടെങ്കില്, bയെ അനുക്രമത്തിന്റെ സീമയെന്ന് പറയുന്നു. ഇതിനെ f(n)=b , f(n) = b. എന്ന് എഴുതും.{1,1/2,1/3,...........}. എന്ന അനുക്രമത്തിന്റെ സീമ 0 ആണ്. എന്തുകൊണ്ടെന്നാല് N (0,ε) എന്ന സാമീപ്യത്തില് അതിലെ അനന്തം അംഗങ്ങള് ഉള്പ്പെടുന്നു. ε എന്ന ധനവാസ്തവികസംഖ്യയെ അപേക്ഷിച്ച് N (0,ε) എന്ന ഗണത്തിനു പുറമേ പോകുന്ന അംഗങ്ങളുടെ എണ്ണം പരിമിതമാണ്. സീമ ഉള്ള അനുക്രമത്തെ അഭികേന്ദ്രസരണമെന്നും അല്ലാത്തതിനെ അപകേന്ദ്രസരണമെന്നും പറയുന്നു. |
| - | + | == കോഷി അനുക്രമങ്ങള് == | |
| - | + | അനുക്രമത്തിലെ ഒരു പരിധിക്കുശേഷമുള്ള പദങ്ങളില് ഏതു രണ്ടെണ്ണവും തമ്മിലുള്ള ദൂരം വളരെ ചെറിയ ഒരു ധനവാസ്തവിക സംഖ്യയ്ക്കു താഴെയായിരിക്കുമെങ്കില് ആ അനുക്രമം ഒരു കോഷി അനുക്രമമായിരിക്കും. അഭികേന്ദ്രസരണം ആയ ഏതു അനുക്രമത്തിന്റെയും ഒരു സാമാന്യ സവിശേഷതയാണിത്. എന്നാല് എല്ലാ മിതീയ ഗണങ്ങളിലും കോഷി അനുക്രമങ്ങള് അഭികേന്ദ്രസരണമാകണമെന്നില്ല. വാസ്തവിക സംഖ്യാഅനുക്രമങ്ങളില് കോഷി അനുക്രമങ്ങള് എല്ലാം അഭികേന്ദ്രസരണങ്ങള് ആണ്. | |
| - | + | === ബോല്സാനോ-വെയര്സ്റ്റ്രോസ് തത്ത്വം=== | |
| - | + | സമതലത്തെ ആസ്പദമാക്കി, അതായത് R<sup>2</sup> എന്ന തലത്തെ സംബന്ധിച്ച്, ഈ തത്ത്വം തെളിയിക്കുന്ന മാര്ഗം ഉപയോഗിച്ചു തന്നെ സാമാന്യമായ യൂക്ളിഡിയാതലങ്ങള്ക്കും പ്രയോഗിക്കാവുന്നതാണ്. ഇതിന്റെ പ്രണേതാക്കള് ബോല്സാനോ, വെയര്സ്റ്റ്രോസ് എന്നീ ഗണിതശാസ്ത്രജ്ഞന്മാരാണ്. | |
| - | |||
| - | + | R<sup>n</sup>-എന്ന n-മാനതലത്തിലെ ഓരോ ബന്ധിത (bounded) അനന്തഗണത്തിനും ഒരു സീമാബിന്ദുവെങ്കിലുമുണ്ട്. | |
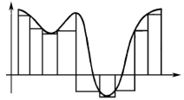
| - | + | A എന്ന ഗണം ബന്ധിതമായതിനാല് അതുള്ക്കൊള്ളുന്ന ഒരു സംവൃത സമചതുരം (S) കണ്ടെത്താന് കഴിയും. ഈ ചതുരത്തെ നാലു തുല്യ സമചതുരങ്ങളായി തിരിക്കാം (ചിത്രം 2). ഇതില് ഏതെങ്കിലുമൊരു ചതുരത്തിന് (S<sub>1</sub>), A-യിലെ അനന്തമായ ഭാഗം ഉള്ക്കൊള്ളാന് കഴിയും. A അനന്തമായതിനാല് ഇതു സാധ്യമാണ്. S<sub>1</sub>-നെ വീണ്ടും നാലു തുല്യഭാഗങ്ങളായി തിരിക്കുക. ഇവയിലൊന്നില് A-യിലെ അനന്തമായ ഭാഗം ഉള്ക്കൊള്ളുന്ന ലഘുചതുരം തുടര്ച്ചയായി കണ്ടെത്തുകയും ചെയ്യാം. അങ്ങനെ S, S<sub>1</sub>, S<sub>2</sub>, S<sub>3</sub> ... എന്നു ചുരുങ്ങിവരുന്ന ഗണങ്ങളുടെ അനുക്രമം ഉണ്ടാകുന്നു. n വര്ധിപ്പിച്ചുകൊണ്ടു പോയാല് S<sub>n</sub>- എന്ന ചതുരത്തിന്റെ വശം ചെറുതായി വരികയും സീമ 0 ആയിത്തീരുകയും ചെയ്യും. S<sub>1</sub>-ല് നിന്ന് (a<sub>1</sub>,b<sub>1</sub>) എന്നൊരു ബിന്ദു, S<sub>2</sub>-ല് നിന്നു മറ്റൊരു ബിന്ദു (a<sub>2</sub>, b<sub>2</sub>), S<sub>3</sub>-ല് നിന്നു (a<sub>3</sub>, b<sub>3</sub>) അങ്ങനെ S<sub>n</sub>-ല് നിന്നു (a<sub>n</sub>, b<sub>n</sub>) (ഈ ബിന്ദുക്കളെല്ലാം വ്യത്യസ്തമാണ്) എന്നിവ ക്രമത്തിലെടുത്താല് അത് ഒരു കോഷി അനുക്രമമായിരിക്കും. S<sub>n</sub>-ന്റെ വശത്തിനു സീമ 0 ആയിരിക്കുന്നതാണ് അതിനു കാരണം. അതുകൊണ്ട് (a,b) എന്നൊരു ബിന്ദു R<sup>2</sup>തലത്തിലുണ്ടാകുന്നു.അതിനുള്ളവ്യവസ്ഥ n സീമ <u>→</u>∞(a<sub>n</sub>,b<sub>n</sub>), = (a, b) എന്നതാണ്. N ((a, b), ε) എന്ന ഓരോ സാമീപ്യത്തിലും A യിലെ (a<sub>n</sub>,b<sub>n</sub>) എന്നീ അനന്തം വ്യത്യസ്ത ബിന്ദുക്കള് ഉള്ക്കൊള്ളുന്നതിനാല്, (a, b) എന്ന ബിന്ദു A യുടെ സീമാബിന്ദുവാണ് (ചിത്രം 2). | |
| - | |||
| - | + | [[Image:p502A.png]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
=== ഫലനത്തിന്റെ സീമ === | === ഫലനത്തിന്റെ സീമ === | ||
| - | A, B എന്നിവ രണ്ടു മിതീയ ഗണങ്ങളായിരിക്കട്ടെ; a, b എന്നിവ A, B ഗണങ്ങളിലെ സ്ഥിരബിന്ദുക്കളും. A ഗണത്തെയോ a ഒഴിവാക്കിക്കൊണ്ടുള്ള A-നെയോ (അതായത് A- {a | + | A, B എന്നിവ രണ്ടു മിതീയ ഗണങ്ങളായിരിക്കട്ടെ; a, b എന്നിവ A, B ഗണങ്ങളിലെ സ്ഥിരബിന്ദുക്കളും. A ഗണത്തെയോ a ഒഴിവാക്കിക്കൊണ്ടുള്ള A-നെയോ (അതായത് A- {a}), B യിലേക്ക് രൂപാന്തരപ്പെടുത്തുന്ന ഫലനമാണ് f. a ഉള്പെടാത്ത A യുടെ സാമീപ്യത്തെ N' (a, ∂) എന്നു സൂചിപ്പിക്കുക. ∂ ഒരു ധനപൂര്ണസംഖ്യയാണെന്നും N' (a, ∂) ശൂന്യഗണമല്ലെന്നും സങ്കല്പിക്കുക. B-ല് N (b, ε) എന്ന bയുടെ ഓരോ സാമീപ്യത്തിനും അനുയോഗമായി A-ല് N' (a, ∂) എന്നൊരു സാമീപ്യം ഉണ്ടാവുകയും N' (a, ∂) യുടെ രൂപാന്തരണമായ f [N' (a,∂) N (b,ε)-ല് ഉള്ക്കൊള്ളുകയും ആണെങ്കില്, f (x)-ന്റെ സീമ b ആണെന്നു പറയുന്നു; x →af(x)=b എന്നു രേഖപ്പെടുത്താം. |
രണ്ടു ഫലനങ്ങളുടെ ആകെത്തുകയുടെയും വ്യത്യാസങ്ങളുടെയും കാര്ത്തീയ ഗുണിതത്തിന്റെയും ഹരണത്തിന്റെയും സീമകള് യഥാക്രമം സീമകളുടെ ആകെത്തുകയും വ്യത്യാസവും ഗുണിതവും ഹരണഫലവുമാണ്; ഹാരകഫലനം ശൂന്യമാകരുതെന്ന നിബന്ധനയുണ്ട്. | രണ്ടു ഫലനങ്ങളുടെ ആകെത്തുകയുടെയും വ്യത്യാസങ്ങളുടെയും കാര്ത്തീയ ഗുണിതത്തിന്റെയും ഹരണത്തിന്റെയും സീമകള് യഥാക്രമം സീമകളുടെ ആകെത്തുകയും വ്യത്യാസവും ഗുണിതവും ഹരണഫലവുമാണ്; ഹാരകഫലനം ശൂന്യമാകരുതെന്ന നിബന്ധനയുണ്ട്. | ||
| - | |||
== അവിച്ഛിന്നത == | == അവിച്ഛിന്നത == | ||
| വരി 145: | വരി 124: | ||
Continuity | Continuity | ||
| - | f(x) എന്ന ഫലനം a എന്ന ബിന്ദുവില് അവിച്ഛിന്നമാകണമെങ്കില് f(a)-ക്ക് നിശ്ചിതമായ ഒരു മൂല്യം ഉണ്ടായിരിക്കണം; മാത്രമല്ല, x എന്ന ചരബിന്ദു a എന്ന ബിന്ദുവിനോട് അടുക്കുന്നതനുസരിച്ച് f(x) എന്ന ഫലനം f(a) എന്ന മൂല്യത്തോട് അടുക്കുകയും വേണം. ഇതു കൃത്യതയോടെ ഇപ്രകാരം പറയാം. | + | f(x) എന്ന ഫലനം a എന്ന ബിന്ദുവില് അവിച്ഛിന്നമാകണമെങ്കില് f(a)-ക്ക് നിശ്ചിതമായ ഒരു മൂല്യം ഉണ്ടായിരിക്കണം; മാത്രമല്ല, x എന്ന ചരബിന്ദു a എന്ന ബിന്ദുവിനോട് അടുക്കുന്നതനുസരിച്ച് f(x) എന്ന ഫലനം f(a) എന്ന മൂല്യത്തോട് അടുക്കുകയും വേണം. ഇതു കൃത്യതയോടെ ഇപ്രകാരം പറയാം. ε ഒരു ധനസംഖ്യയാണെങ്കില് അതിനു ബന്ധപ്പെട്ട് δഎന്ന ഒരു ധനസംഖ്യ ഉണ്ടായിരിക്കുകയും |x-a | <δആകുമ്പോഴെല്ലാം |f(x) - f(a)| < ε ആകുകയും ചെയ്താല് f(x) എന്ന ഫലനം a-ല് അവിച്ഛിന്നമാണെന്നു പറയും. ഒരു പ്രദേശത്തുള്ള ഓരോ ബിന്ദുവിലും ഒരു ഫലനം അവിച്ഛിന്നമാണെങ്കില് മാത്രമേ ആ പ്രദേശത്തില് ആ ഫലനം അവിച്ഛിന്നം ആണെന്നു പറയാവൂ. |
| - | + | ||
അവിച്ഛിന്നമായ ഒരു ഫലനത്തിന്റെ രണ്ടു മൂല്യങ്ങള്ക്കിടയിലുള്ള ഒരു മൂല്യത്തിന് ചേരുന്നവിധം ആ മൂല്യങ്ങള്ക്ക് ആധാരമായ ബിന്ദുക്കള്ക്കിടയില് ഒരു ബിന്ദു ഉണ്ടായിരിക്കും. | അവിച്ഛിന്നമായ ഒരു ഫലനത്തിന്റെ രണ്ടു മൂല്യങ്ങള്ക്കിടയിലുള്ള ഒരു മൂല്യത്തിന് ചേരുന്നവിധം ആ മൂല്യങ്ങള്ക്ക് ആധാരമായ ബിന്ദുക്കള്ക്കിടയില് ഒരു ബിന്ദു ഉണ്ടായിരിക്കും. | ||
| വരി 154: | വരി 132: | ||
Uniform continuity | Uniform continuity | ||
| - | ഫലനത്തിന്റെ സീമയിലും അവിച്ഛിന്നതയിലും സൂചിപ്പിച്ചിരുന്ന | + | ഫലനത്തിന്റെ സീമയിലും അവിച്ഛിന്നതയിലും സൂചിപ്പിച്ചിരുന്ന ∂,εഎന്നീ ധനവാസ്തവിക സംഖ്യകള് പരസ്പരം ബന്ധപ്പെട്ടിരിക്കുന്നു. എന്നു മാത്രമല്ല ε a എന്ന ബിന്ദുവിനെയും ആശ്രയിച്ചിരിക്കുന്നതാണ് അവിച്ഛിന്നതയില് കാണുന്നത്. എന്നാല് ∂ a എന്ന ബിന്ദുവിനെ ആശ്രയിക്കാതെ തന്നെ ε-നുമായി മാത്രം ബന്ധപ്പെട്ടിരിക്കുകയെന്ന വ്യവസ്ഥയില് അവിച്ഛിന്നതയുണ്ടാകുമ്പോള് അതിന് ഏകതാന-അവിച്ഛിന്നതയെന്നു പറയുന്നു. ഏകതാന-അവിച്ഛിന്നമായ ഫലനം അവിച്ഛിന്നവുമാണ്. ഏകതാന-അവിച്ഛിന്നത അനാലിസിസില് വളരെ പ്രാധാന്യമുള്ള ആശയമാണ്. |
==വ്യുത്പന്നം== | ==വ്യുത്പന്നം== | ||
| വരി 160: | വരി 138: | ||
Derivative | Derivative | ||
| - | R-ല്നിന്നുള്ള ഒരു ഗണത്തെ | + | R-ല്നിന്നുള്ള ഒരു ഗണത്തെ R-ലേക്കുതന്നെ രൂപാന്തരണം ചെയ്യുന്ന ഫലനമാണ് f എങ്കില് R-ലുള്ള ഓരോ ബിന്ദു (a) വിനും f '(a) എന്നതു നിര്വചിക്കുന്നത് ഇപ്രകാരമാണ്: h പൂജ്യത്തെ സമീപിക്കുന്ന ഒരുചരമാണ്, f(a + h)-ഉം f(a)ഉം തമ്മി ലുള്ള വ്യത്യാസത്തെ h കൊണ്ടു ഹരിച്ചുകിട്ടുന്ന ഫലത്തിന് h പൂജ്യത്തോട് അടുക്കുമ്പോള് സീമയുണ്ടെങ്കില് അതിനു f '(a) എന്നു സൂചിപ്പിക്കുകയും f-ന്റെ a-യിലെ വ്യുത്പന്നമെന്നു വിളിക്കുകയും ചെയ്യുന്നു. അതായത് |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | [[Image:p502.png]] | |
| - | + | ||
| - | + | ||
| - | + | h പൂജ്യത്തിലേക്കടുക്കുമ്പോള്, PQ എന്ന ജ്യാവ് (chord) | |
y = f(x) എന്ന രേഖയ്ക്കു P യിലുള്ള സ്പര്ശകമായി മാറുന്നു. അതുകൊണ്ട് f '(a) എന്നത് ഈ സ്പര്ശകത്തിന്റെ ചരിവുമാനം (slope) ആണ് (ചിത്രം 3). | y = f(x) എന്ന രേഖയ്ക്കു P യിലുള്ള സ്പര്ശകമായി മാറുന്നു. അതുകൊണ്ട് f '(a) എന്നത് ഈ സ്പര്ശകത്തിന്റെ ചരിവുമാനം (slope) ആണ് (ചിത്രം 3). | ||
| വരി 180: | വരി 150: | ||
Mean value theorem | Mean value theorem | ||
| - | മാധ്യമൂല്യതത്ത്വത്തിന്റെ മുന്നോടിയായി ചില വ്യവസ്ഥകള് ക്കനുസരിച്ച് f എന്ന ഫലനത്തിന്റെ വ്യുത്പന്നം പൂജ്യമാകുന്ന ഘട്ടമാണ് റോള് തത്ത്വത്തില് (Rolle's Theorem) പ്രതിപാദിക്കുന്നത്; (a, b) എന്ന വിവൃതാന്തരാളത്തിലെ ഏത് സാമാന്യബിന്ദുവായ x-നും f '(x) ഉണ്ടായിരിക്കുക; | + | മാധ്യമൂല്യതത്ത്വത്തിന്റെ മുന്നോടിയായി ചില വ്യവസ്ഥകള് ക്കനുസരിച്ച് f എന്ന ഫലനത്തിന്റെ വ്യുത്പന്നം പൂജ്യമാകുന്ന ഘട്ടമാണ് റോള് തത്ത്വത്തില് (Rolle's Theorem) പ്രതിപാദിക്കുന്നത്; (a, b) എന്ന വിവൃതാന്തരാളത്തിലെ ഏത് സാമാന്യബിന്ദുവായ x-നും f '(x) ഉണ്ടായിരിക്കുക; [a b ] എന്ന സംവൃതാന്തരാളത്തില് f അവിച്ഛിന്നമായിരിക്കുക; f(a), f(b) എന്നിവ തുല്യമായിരിക്കുക - ഈ വ്യവസ്ഥിതിയില് f '(z) പൂജ്യമാകുന്ന വിധം (a, b) ല് z എന്നൊരു ബിന്ദുവുണ്ടായിരിക്കും. ഇതാണ് റോള് തത്ത്വം. ഇതിലെ ആദ്യത്തെ രണ്ടു വ്യവസ്ഥകള് മാത്രമായാല്, |
| - | + | f'(z) = f(b)-f(a)/b-a | |
| - | + | ||
| - | + | [[Image:p.no.476.jpg|thumb|200x100px|right|ചിത്രം3]] | |
| - | [[Image:p.no.476.jpg|thumb|200x100px|right| | + | |
ആയിരിക്കുന്ന വിധം (a, b) എന്ന വിവൃതാന്തരാളത്തില് ഉള്ക്കൊള്ളുന്ന ഒരു ബിന്ദു (z) ഉണ്ടായിരിക്കും. ഇതാണ് മാധ്യമൂല്യതത്ത്വം. സാമാന്യവത്കരിക്കപ്പെട്ടിട്ടുള്ള ഈ തത്ത്വത്തിന് ധാരാളം വ്യാഖ്യാനങ്ങള് ഉണ്ടായിട്ടുണ്ട്. ഒരു പൊതുതത്ത്വം ഇവിടെ ചേര്ക്കാം. f(x), g(x) എന്നിവ (a, b)-ല് അവകലനക്ഷമവും (അതായത് f '(x), g'(x) ഉണ്ടായിരിക്കുക) a, b എന്നീ ബിന്ദുക്കളില് f അവിച്ഛിന്നവുമാണെങ്കില്, (a, b)-യിലെ ഏതു x-നും g' (x) പൂജ്യമല്ലാത്തിടത്തോളം, | ആയിരിക്കുന്ന വിധം (a, b) എന്ന വിവൃതാന്തരാളത്തില് ഉള്ക്കൊള്ളുന്ന ഒരു ബിന്ദു (z) ഉണ്ടായിരിക്കും. ഇതാണ് മാധ്യമൂല്യതത്ത്വം. സാമാന്യവത്കരിക്കപ്പെട്ടിട്ടുള്ള ഈ തത്ത്വത്തിന് ധാരാളം വ്യാഖ്യാനങ്ങള് ഉണ്ടായിട്ടുണ്ട്. ഒരു പൊതുതത്ത്വം ഇവിടെ ചേര്ക്കാം. f(x), g(x) എന്നിവ (a, b)-ല് അവകലനക്ഷമവും (അതായത് f '(x), g'(x) ഉണ്ടായിരിക്കുക) a, b എന്നീ ബിന്ദുക്കളില് f അവിച്ഛിന്നവുമാണെങ്കില്, (a, b)-യിലെ ഏതു x-നും g' (x) പൂജ്യമല്ലാത്തിടത്തോളം, | ||
| - | + | f'(z)/g'(z) =f(b)-f(a)/g(b)-g(a) | |
| - | + | ||
| - | + | ||
ആയിരിക്കുന്നവിധം (a,b)-ല് ഒരു ബിന്ദു (z) ഉണ്ടായിരിക്കും. f(a), g(a) എന്നിവ 0 ആയിരിക്കുമ്പോള് | ആയിരിക്കുന്നവിധം (a,b)-ല് ഒരു ബിന്ദു (z) ഉണ്ടായിരിക്കും. f(a), g(a) എന്നിവ 0 ആയിരിക്കുമ്പോള് | ||
| - | + | f'(z) / g'(z) = f(b)/ g (b) | |
| - | + | ||
| - | + | ||
| - | + | ||
ആയിത്തീരും. | ആയിത്തീരും. | ||
| വരി 203: | വരി 168: | ||
ഇവിടെ a,x എന്നിവയ്ക്കിടയിലാണ് z അതുകൊണ്ട് x a-യിലേക്ക് അടുക്കുമ്പോള് z എന്ന ചരവും aയെ സമീപിക്കുന്നു. | ഇവിടെ a,x എന്നിവയ്ക്കിടയിലാണ് z അതുകൊണ്ട് x a-യിലേക്ക് അടുക്കുമ്പോള് z എന്ന ചരവും aയെ സമീപിക്കുന്നു. | ||
| - | + | [[Image:p503a.png]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
== ആംശികാവകലനവും സമ്പൂര്ണാവകലനവും == | == ആംശികാവകലനവും സമ്പൂര്ണാവകലനവും == | ||
| വരി 218: | വരി 174: | ||
Partial differentiation and Total differentiation | Partial differentiation and Total differentiation | ||
| - | x,y എന്നീ രണ്ടു സ്വതന്ത്രചരങ്ങളെ ആശ്രയിച്ചിരിക്കുന്ന ഫലനം f | + | x,y എന്നീ രണ്ടു സ്വതന്ത്രചരങ്ങളെ ആശ്രയിച്ചിരിക്കുന്ന ഫലനം f R<sup>2</sup>-ലെ ഒരു വിവൃതഗണമായ A-യെ R-ലേക്കു രൂപാന്തരണം ചെയ്യുന്നുവെന്നു കരുതുക. z = f(x,y). x,y എന്നിവയില് ഏതെങ്കിലും ഒന്നിനെ മാത്രം സ്ഥിരമായി നിര്ത്തി, മറ്റേചരത്തെ ആശ്രയിച്ചു ഫലനമൂല്യത്തിലുണ്ടാകുന്ന വ്യതിയാനത്തിന്റെ സീമ കണ്ടുപിടിക്കാന് കഴിയും. ഈ സീമയാണ് ആംശിക അവകലജാങ്കം (partial differential coefficient). |
| - | + | [[Image:p503b.png]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
എന്നു തുടങ്ങിയ ചിഹ്നങ്ങള്കൊണ്ടാണ് ആംശിക അവകലജാങ്കം സൂചിപ്പിക്കുന്നത്. x,y എന്നീ രണ്ടു സ്വതന്ത്രചരങ്ങളുടെ വ്യത്യാസങ്ങളും f(x,y) എന്ന ഫലനത്തെ സ്വാധീനിക്കാം. ആ സ്വാധീനത്തിന്റെ ഒരളവാണ് സമ്പൂര്ണാവകലനം. | എന്നു തുടങ്ങിയ ചിഹ്നങ്ങള്കൊണ്ടാണ് ആംശിക അവകലജാങ്കം സൂചിപ്പിക്കുന്നത്. x,y എന്നീ രണ്ടു സ്വതന്ത്രചരങ്ങളുടെ വ്യത്യാസങ്ങളും f(x,y) എന്ന ഫലനത്തെ സ്വാധീനിക്കാം. ആ സ്വാധീനത്തിന്റെ ഒരളവാണ് സമ്പൂര്ണാവകലനം. | ||
| വരി 234: | വരി 182: | ||
സമ്പൂര്ണാവകലനത്തെ ഇങ്ങനെ പ്രകടിപ്പിക്കാം: | സമ്പൂര്ണാവകലനത്തെ ഇങ്ങനെ പ്രകടിപ്പിക്കാം: | ||
| - | + | df = df(x,y; h, k) = f<sub>x</sub>(x,y) h + f<sub>y</sub> (x,y) k അഥവാ | |
| + | |||
| + | dz = f<sub>x</sub> (x,y) dx + f<sub>y</sub> (x, y) dy. | ||
| - | |||
| - | |||
== സമാകലനം == | == സമാകലനം == | ||
Integration | Integration | ||
| വരി 245: | വരി 193: | ||
=== വിഭജനം === | === വിഭജനം === | ||
| - | + | [a, b]എന്നത് R-ന്റെ ഒരു സംവൃത-അന്തരാളമാണെന്നു കരുതുക. a = x<sub>0</sub>, x<sub>1</sub>, x<sub>2</sub>, ....x<sub>1-1</sub>, x<sub>1</sub>, .....x<sub>n</sub> = b എന്നീ ബിന്ദുക്കള് [a, b]യെ വിഭജിക്കുന്നു. ഇവിടെ x<sub>1-1</sub> നെക്കാള് വലിയതാണ് x<sub>1</sub>;[a,b], -ല് അവിച്ഛിന്നവും ബന്ധിതവുമാണ് f. m,M, എന്നിവ ക്രമത്തില് [a, b]യുടെ നിമ്നവും ഉന്നതവുമായ പരിധികളാണ് (lower and upper bounds). f([x<sub>1-1</sub>,x<sub>1</sub>)-ന്റെ ഇന്ഫിമം ആയ m<sub>i</sub> (i= 1,2,....n) എല്ലാം m-നും M-നും ഇടയിലായിരിക്കും.m (b-a) ക്കാള് വലുതാണ് S = m<sub>1</sub> (x<sub>1</sub> -x<sub>0</sub>) + m<sub>2</sub> (x<sub>2</sub>-x<sub>1</sub>) +...+m<sub>n</sub>(x<sub>n</sub>-x<sub>n-1</sub>) ഈ സംഖ്യയെക്കാള് വലുതാണ് M (b-a). അതുകൊണ്ട് S ബന്ധിതമാണ്. S-ന്റെ സുപ്രീമം<sup>b</sup>∫ | |
| + | <sub>a</sub>fdx എന്നു സൂചിപ്പിച്ചാല്, അത് (b-a) [m,M]-ല് ഉള്പ്പെടുന്നു എന്നു സിദ്ധിക്കുന്നു. a,b -യെക്കാള് വലുതാകുമ്പോള് <sup>b</sup>∫<sub>a</sub> fdx എന്നത് - <sup>a</sup>∫<sub>b</sub>fdxആയും a, bഎന്നിവ തുല്യമാകുമ്പോള് 0 ആയും നിര്വചിക്കപ്പെടാമെങ്കില്, <sup>a</sup>∫<sub>b</sub>fdx എന്നതാണ് [a, b] എന്ന സംവൃത അന്തരാളത്തില് f-ന്റെ സ്ഥിരസമാകലം (Definite integral) എന്നു പറയാം. | ||
| - | ഈ സമാകലത്തെ പ്രതിലോമ വ്യുത്പന്നമായി കാണിക്കാന് കഴിയും.F(x) ന്റെ അവകലനമാണ് f(x) എങ്കില് | + | ഈ സമാകലത്തെ പ്രതിലോമ വ്യുത്പന്നമായി കാണിക്കാന് കഴിയും.F(x) ന്റെ അവകലനമാണ് f(x) എങ്കില് ∫<sup>b</sup><sub>a</sub>fdx= F(b)-F(a) ആയിരിക്കും. (ചിത്രം 4). |
| - | [[Image:p.no.476a.jpg|thumb|250x100px|centre| | + | [[Image:p.no.476a.jpg|thumb|250x100px|centre|ചിത്രം4]] |
== അനുക്രമങ്ങളും ശ്രേണികളും == | == അനുക്രമങ്ങളും ശ്രേണികളും == | ||
| - | നിസര്ഗസംഖ്യാഗണത്തിലുള്ള അംഗങ്ങളെ രൂപാന്തരപ്പെടുത്തുന്ന ഫലനമാണ് അനുക്രമം: അതായത്, | + | നിസര്ഗസംഖ്യാഗണത്തിലുള്ള അംഗങ്ങളെ രൂപാന്തരപ്പെടുത്തുന്ന ഫലനമാണ് അനുക്രമം: അതായത്, a<sub>1</sub>, a<sub>2</sub>, .....a<sub>n</sub>,......}. വാസ്തവിക സംഖ്യാഗണ(R)ത്തിലേക്കാണ് രൂപാന്തരണമെങ്കില് ആ അനുക്രമം വാസ്തവികവും, സമ്മിശ്രസംഖ്യാഗണത്തിലേക്കാണെങ്കില് സമ്മിശ്രസംഖ്യാനുക്രമ(complex sequence)വും ആണ്. അനുക്രമത്തെ (S<sub>n</sub>) എന്നു സൂചിപ്പിക്കാം. |
=== അഭികേന്ദ്രസരണവും അപകേന്ദ്രസരണവും === | === അഭികേന്ദ്രസരണവും അപകേന്ദ്രസരണവും === | ||
| - | ( | + | (S<sub>n</sub>) എന്ന അനുക്രമത്തിലെ ആദ്യത്തെ ഏതാനും ക്ലുപ്തമായ പദങ്ങളൊഴിച്ച് ബാക്കി ക്രമത്തില് ശേഷിക്കുന്നവയെല്ലാം S-ന്റെ ഒരു സാമീപ്യത്തില് ഉള്പ്പെടുമെങ്കില് 'S-ലേക്ക് (S<sub>n</sub>) അടുക്കുന്നു' എന്നു പറയാം. സാങ്കേതികമായി പറഞ്ഞാല്, S എന്ന ബിന്ദുവിന്റെ ഒരുസിദ്ധസാമീപ്യമായ N (s, k)-ല് {S<sub>n</sub> : n≥ m} ഉള്പ്പെടുന്നവിധം m എന്നൊരു നിസര്ഗസംഖ്യ കണ്ടുപിടിക്കാന് സാധിക്കുമെങ്കില്, (S<sub>n</sub>) S-ലേക്ക് അടുക്കുന്നു. ഈ ആശയം n → ∞ |
| - | + | S<sub>n</sub> = S,എന്നോ ,' S<sub>n</sub> → S,എന്നോ പ്രകടിപ്പിക്കാവുന്നതാണ്. n അനന്തമായി തുടര്ന്നുപോകുമ്പോള് സ്ഥിരമായ ഒരു സീമ (S) കല്പിക്കാമെങ്കില്, (S<sub>n</sub>) എന്ന അനുക്രമം അഭികേന്ദ്രസരണവും അല്ലാത്തത് അപകേന്ദ്രസരണവും ആണ്. അപകേന്ദ്രസരണത്തില് സീമ S<sub>n</sub> എന്നതിനര്ഥമില്ല; അത് അനന്തമാണ്. (S<sub>n</sub> ), (t<sub>n</sub> ) എന്നീ അനുക്രമങ്ങളുടെ സീമകള് ക്രമത്തില് s,t ആണെങ്കില്, | |
| - | + | S<sub>n</sub> + t<sub>n</sub>, S<sub>n</sub>t<sub>n</sub>, k S<sub>n</sub>,S<sub>n</sub>/t<sub>n</sub>(t<sub>n</sub>≠0) | |
എന്നിവയുടെ സീമകള് ക്രമത്തില് | എന്നിവയുടെ സീമകള് ക്രമത്തില് | ||
| - | + | ||
| - | + | S + t, St, kS, t (t ≠0 ) | |
| - | ആയിരിക്കും.∑S<sub>n</sub>, അഭികേന്ദ്രസരണമാണെങ്കില് s<sub>n</sub>-ന്റെ സീമ 0 ആണ്. അഭികേന്ദ്രസരണമാകാനുള്ള വ്യവസ്ഥകള് : (1) ∑S<sub>n</sub> ലെ എല്ലാ പദങ്ങളും ധനാത്മകമാണെങ്കില്, ∑S<sub>n</sub> ബന്ധിതമായാല് അഭികേന്ദ്രസരണവുമായിരിക്കും; (2) താരതമ്യപരീക്ഷണം (comparison test). ∑b<sub>n</sub> അഭികേന്ദ്രസരണവും ഒരു പരിധിക്കുശേഷം വരുന്ന പദങ്ങള് തമ്മില് 0&le a<sub>n</sub>&le b<sub>n</sub> എന്ന ബന്ധവുമുണ്ടെങ്കില്, ∑a<sub>n</sub> അഭികേന്ദ്രസരണമായിരിക്കും; (3) ∑| a<sub>n</sub> | അഭികേന്ദ്രസരണമാണെങ്കില് ∑a<sub>n</sub> നിരപേക്ഷ അഭികേന്ദ്രസരണമായിരിക്കും; (4) നിരപേക്ഷ അഭികേന്ദ്രസരണത്തില് അഭികേന്ദ്രസരണം ഉള്ക്കൊള്ളുന്നു; (5) ∑b<sub>n</sub> അഭികേന്ദ്രസരണം ആണെങ്കില് നിരപേക്ഷ ∑a<sub>n</sub> അഭികേന്ദ്രസരണമാണ്; (6) അംശബന്ധപരീക്ഷണം (Ratio test). ∑a<sub>n</sub> അനുക്രമത്തിന്റെ ഒരു പദവും അതിനു മുമ്പുള്ള പദവും തമ്മിലുള്ള അംശബന്ധത്തിന്റെ കേവലമൂല്യം ഏതെങ്കിലും ഒരു പരിധിക്കുശേഷം ഒരു ധനഭിന്നമാണെങ്കില്, അതായത് | + | ആയിരിക്കും.∑S<sub>n</sub>, അഭികേന്ദ്രസരണമാണെങ്കില് s<sub>n</sub>-ന്റെ സീമ 0 ആണ്. അഭികേന്ദ്രസരണമാകാനുള്ള വ്യവസ്ഥകള് : (1) ∑S<sub>n</sub> ലെ എല്ലാ പദങ്ങളും ധനാത്മകമാണെങ്കില്, ∑S<sub>n</sub> ബന്ധിതമായാല് അഭികേന്ദ്രസരണവുമായിരിക്കും; (2) താരതമ്യപരീക്ഷണം (comparison test). ∑b<sub>n</sub> അഭികേന്ദ്രസരണവും ഒരു പരിധിക്കുശേഷം വരുന്ന പദങ്ങള് തമ്മില് 0 ≤ a<sub>n</sub> ≤ b<sub>n</sub> എന്ന ബന്ധവുമുണ്ടെങ്കില്, ∑a<sub>n</sub> അഭികേന്ദ്രസരണമായിരിക്കും; (3) ∑| a<sub>n</sub> | അഭികേന്ദ്രസരണമാണെങ്കില് ∑a<sub>n</sub> നിരപേക്ഷ അഭികേന്ദ്രസരണമായിരിക്കും; (4) നിരപേക്ഷ അഭികേന്ദ്രസരണത്തില് അഭികേന്ദ്രസരണം ഉള്ക്കൊള്ളുന്നു; (5) ∑b<sub>n</sub> അഭികേന്ദ്രസരണം ആണെങ്കില് നിരപേക്ഷ ∑a<sub>n</sub> അഭികേന്ദ്രസരണമാണ്; (6) അംശബന്ധപരീക്ഷണം (Ratio test). ∑a<sub>n</sub> അനുക്രമത്തിന്റെ ഒരു പദവും അതിനു മുമ്പുള്ള പദവും തമ്മിലുള്ള അംശബന്ധത്തിന്റെ കേവലമൂല്യം ഏതെങ്കിലും ഒരു പരിധിക്കുശേഷം ഒരു ധനഭിന്നമാണെങ്കില്, അതായത് |
| - | + | [[Image:p504a.png]] | |
| - | + | ||
| + | ആണെങ്കില് ∑a<sub>n</sub>നിരപേക്ഷ അഭികേന്ദ്രസരണമാണ്; ഈ അംശബന്ധം 1-നെക്കാള് കൂടുതല് ആണെങ്കില് ∑a<sub>n</sub> അപകേന്ദ്രസരണവുമാണ്. | ||
| - | ആണെങ്കില് & | + | |a<sub>n+1</sub>/a<sub>n</sub>|നുപകരം അതിന്റെ സീമയെടുത്താലും ഈ നിയമം അനുസരിക്കാവുന്നതാണ്; എന്നാല് സീമയുടെ മൂല്യം ഒന്ന് ആണെങ്കില് പരീക്ഷണം പരാജയപ്പെടുന്നു; (7) സമാകല പരീക്ഷണം (integral test). f ഒരു വാസ്തവിക ഫലനമാണ്; [1,∞) എന്ന ഗണത്തില് അവിച്ഛിന്നവും മൂല്യശോഷണവുമുള്ളതുമാണ്; ധനാത്മകവുമാണ്. a<sub>n</sub> ആയിരിക്കെ<sup>n</sup> ∫<sub>1</sub> അഭികേന്ദ്രസരണമാണെങ്കില് മാത്രമേ, ∑a<sub>n</sub> അഭികേന്ദ്രസരണമാകയുള്ളു, |
| + | [[Image:p504b.png]] | ||
| - | + | [[Image:p.no.477.jpg|thumb|150x150px|right|ചിത്രം5]] | |
| - | [[Image:p.no.477.jpg|thumb|150x150px|right| | + | |
എന്ന സമവാക്യം ഉപയോഗിച്ചാണ് ഇതു തെളിയിക്കുന്നത്; | എന്ന സമവാക്യം ഉപയോഗിച്ചാണ് ഇതു തെളിയിക്കുന്നത്; | ||
| - | (8) ( | + | (8) (-∞ ,1] എന്ന ഗണത്തില് p പെടുന്നെങ്കില്,∑n<sup>-p</sup> അപകേന്ദ്രസരണവും (1, ∞) ല് പെടുന്നെങ്കില്, അഭികേന്ദ്രസരണവുമാണ്. |
| + | [[Category:ഗണിതം]] | ||
Current revision as of 10:01, 24 നവംബര് 2014
ഉള്ളടക്കം |
അനാലിസിസ് (ഗണിതം)
Analysis
ഗണിതശാസ്ത്രതത്ത്വങ്ങളെ അടിസ്ഥാനപരമായി വിശകലനം ചെയ്യുന്ന ശാഖ. ഗണിതശാസ്ത്രത്തിന്റെ മറ്റു ശാഖകളാണ് ജ്യാമിതി അഥവാ ക്ഷേത്രഗണിതം (Geometry), ടോപോളജി (Topology), ബീജഗണിതം (Algebra), അങ്കഗണിതം (Arithmetic) എന്നിവ. എല്ലാ ശാഖകളിലേക്കും വ്യാപിക്കുന്ന ബൃഹത്തായ വളര്ച്ചയാണ് 19-ാം ശ. മുതല് അനാലിസിസിന് ഉണ്ടായിട്ടുള്ളത്. വിശ്ളേഷണം അഥവാ വിശ്ളേഷികം എന്നും ഈ ഗണിതശാഖയെ വിളിക്കുന്നു.
ചരിത്രം
ഗണിതശാസ്ത്രത്തില് പ്രാചീനകാലത്തു ഗ്രീസിലും ഇന്ത്യയിലുമുണ്ടായിട്ടുള്ള ജ്യാമിതീയവും ബീജഗണിതപരവുമായ വളര്ച്ച അനാലിസിസിന്റെ അന്തര്ധാരകളായിരിക്കാമെങ്കിലും എ.ഡി. 1600 മുതലാണ് ഇതു ശ്രദ്ധാര്ഹമായ ഒരു ശാസ്ത്രശാഖയായിത്തീര്ന്നത്. ബലതന്ത്ര (Mechanics)ത്തിന്റെയും താത്ത്വികഭൌതിക (Theoretical Physics)ത്തിന്റെയും അവശ്യ വളര്ച്ചയ്ക്കാധാരമായിട്ടാണ് ഈ ശാഖയുണ്ടായത്. അവകലനവും സമാകലനവും (Diiferentiation and integration), സാധാരണ അവകലസമവാക്യങ്ങളും വ്യതിയാനകലനവും (Ordinary Differential equations and Different Calculus) ബലതന്ത്രത്തിനുവേണ്ടിയാണുണ്ടായത്. ധ്വാനിക (Acoustics)ത്തില് നിന്നും താപഗതിക (Thermodynamics)ത്തില് നിന്നും ഫൂറിയേ ശ്രേണി(Fourier series)യും പ്രകാശിക(Optics)ത്തില്നിന്ന് സമ്മിശ്ര വിശ്ളേഷണവും (Complex Analysis), ഇലാസ്തികത (Elasticity), ദ്രവഗതികം (Hydrodynamics), വിദ്യുത്ഗതികം (Electrodynamics) എന്നിവയില് നിന്ന് ആംശിക-അവകലവാക്യങ്ങളും (Partial Diiferential equations) പ്രേരിതമായെന്നു സാമാന്യമായി പറയാം. 19-ാം ശ.-ത്തില് ബലതന്ത്രം, താപഗതികം എന്നിവയിലെ സാംഖ്യികദര്ശനങ്ങളില്നിന്നാണ് സാംഖ്യികസംഭാവ്യത (Statistical probability) പോലും ഉണ്ടായതെന്നവാദം നിലവിലുണ്ട്. ശാസ്ത്രജ്ഞന്മാരായ ഐസക് ന്യൂട്ടനും (1642-1727) ഗോട്ഫ്രീഡ് ലൈബ്നിറ്റ്സും (1646-1716) കലന(Calculus)ത്തിന്റെ നിശ്ചിതമായ മാര്ഗങ്ങള് കണ്ടെത്തിയതോടെയാണ് അനാലിസിസ് സര്വശാസ്ത്രവ്യാപിയായ ഒരു വിജ്ഞാനശാഖയായിത്തീര്ന്നത്.
സ്വഭാവം
അവകലനവും സമാകലനവും അനാലിസിസിലെ അടിസ്ഥാനമാര്ഗങ്ങളാണെങ്കിലും അനന്തത (Infinity) ആണ് അടിസ്ഥാനതത്ത്വം. വാസ്തവത്തില് ഗണിതശാസ്ത്രം തന്നെ അനന്തതകളുടെ പഠനമാണെന്നു പറയാം. പരിമിതമായ കാര്യങ്ങള് മിക്കവയും പ്രാഥമികഗണിതത്തില് കഴിഞ്ഞാല് അവശേഷിക്കുന്ന തൊണ്ണൂറു ശ.മാ.വും അനന്തത ഉള്ക്കൊള്ളുന്ന പഠനങ്ങളാണ്. അനന്തമായ വലുപ്പം, അനന്തസൂക്ഷ്മം, അനന്തസാമീപ്യം, അനന്തമായ ഉപവിഭജനം എന്നിവയും അനന്ത-അനുക്രമം, അനന്തശ്രേണി, ഫലനം, ഫലനത്തിന്റെ അവിച്ഛിന്നത, ഫലനത്തിന്റെ വ്യുത്പന്നം (derivative), ഫലനത്തിന്റെ സമാകലം (Integral) എന്നിവയുമാണ് വിശ്ളേഷണത്തില് സ്പര്ശിക്കപ്പെടുന്ന കാര്യങ്ങള്. അവകലജഗുണാങ്കം (differential) ഗണിത തത്ത്വങ്ങളിലെന്നല്ല, സാമ്പത്തികശാസ്ത്രം പോലുള്ള എല്ലാ വിജ്ഞാനശാഖകളിലും മൌലികപ്രാധാന്യമര്ഹിക്കുന്ന ആശയമാണ്.
വാസ്തവിക സംഖ്യകള്
ശാസ്ത്രതത്ത്വങ്ങള് ഗണിതത്തിന്റെ ഭാഷയില് അവതരിപ്പിക്കുമ്പോള് അവയ്ക്കു പ്രത്യേകമായ തെളിമയും കൃത്യതയുമുണ്ടാകുന്നു. യുക്തിയുക്തമായ ഒരു പരസ്പരബന്ധം ആ തത്ത്വങ്ങള് തമ്മില് സ്ഥാപിച്ചിരിക്കുന്നതായി മനസ്സിലാക്കാനും കഴിയുന്നു. ഭൌതികശാസ്ത്രത്തിലെ ധ്വാനികം, ദ്രവഗതികം, വൈദ്യുതീപ്രാകാശികം എന്നിവയിലെല്ലാം തരംഗങ്ങളുടെ ഗതിവിഗതികള് മിക്കവാറും ഒരേതരത്തിലുള്ള അവകലസമവാക്യങ്ങള്കൊണ്ടു സൂചിപ്പിക്കാവുന്നതാണ്. ശാസ്ത്രീയ വിവരണങ്ങള് സംഖ്യകളിലൂടെയാണ് പ്രകടമാവുന്നത്; അതായത്; വാസ്തവിക സംഖ്യകളിലൂടെ പ്രകടമാകുന്ന ശാസ്ത്രസത്യങ്ങള് കൂടുതല് വ്യക്തവും കണിശവുമായിരിക്കും. സംഖ്യകളിലൂടെയുള്ള പ്രകടനസമ്പ്രദായം 17-ാം ശ.-ത്തിലാണ് നടപ്പായതെന്നു പറയാം. 20-ാം ശ.ത്തോടെ വാസ്തവിക പൂര്ണസംഖ്യകളോ സംഖ്യകള് തന്നെയോ കൂടാതെ ഭൌതിക സത്യങ്ങള് വെളിപ്പെടുത്തുന്ന സമ്പ്രദായം വളര്ന്നിട്ടുണ്ട്. 'അതീതഗണിതശാസ്ത്ര' (Meta Mathematics) ത്തിന്റെ ഉപജ്ഞാതാക്കള് സംഖ്യാപ്രകടന സമ്പ്രദായത്തില് അതീവ സംശയാലുക്കളാണ്. സംഖ്യകളിലൂടെ ശാസ്ത്രസത്യങ്ങള് പോലും കാണുന്നതില് വളരെ അപകാതയുണ്ടെന്ന് ഈ നൂതന ഗണിതശാഖയിലൂടെ തെളിയിക്കാനുള്ള ശ്രമം ഉണ്ടായിട്ടുണ്ട്.
ബി.സി. 5-ഉം 4-ഉം ശ.-ങ്ങളില് ഗ്രീക്കുകാര് അനാലിസിസിലെ അതിപ്രധാനമായ ചില പ്രശ്നങ്ങള്ക്കു പരിഹാരം നല്കി. √2 ഒരു വിഗണസംഖ്യയാണ് (irrational number: അനാനുപാതികസംഖ്യ). ഗ്രീസിലും ഇന്ത്യയിലും π = 3.14159.... എന്ന വിഗണസംഖ്യയെക്കുറിച്ചുള്ള പഠനങ്ങളുണ്ടായി. വ്യാസാര്ധം 1 ആയിട്ടുള്ള വൃത്തത്തിന്റെ വിസ്തീര്ണം ആണ് π വൃത്തത്തിനു തുല്യവ്യാപ്തിയുള്ള ചതുരം നിര്മിക്കുന്ന പ്രശ്നത്തിനു പ്രാചീനകാലത്തുതന്നെ ഉത്തരം കണ്ടെത്താന് പരിശ്രമം ആരംഭിച്ചിരുന്നു. ഈ വഴിക്കുള്ള പരിശ്രമങ്ങളെല്ലാം 17-ാം ശ.-ത്തിലെ സമാകലസിദ്ധാന്തത്തിനും കലനത്തിന്റെ താത്വികവളര്ച്ചയ്ക്കും കാരണമായി.
ഗണസിദ്ധാന്ത(Set Theory)ത്തിന്റെ ആവിര്ഭാവത്തോടെ അതിസൂക്ഷ്മത (infinitely small), അത്യനന്തം (infinitely large) എന്നീ ആശയങ്ങള്ക്കു പുതിയ ഭാവങ്ങളുണ്ടായി. അനാലിസിസ് മനസ്സിലാക്കാന് അവശ്യം അറിഞ്ഞിരിക്കേണ്ടത് ഗണസിദ്ധാന്തമാണ്. ക്ളാസിക്കല് അനാലിസിസ് ഗണസിദ്ധാന്തത്തെ ആശ്രയിക്കുന്നില്ലെങ്കിലും അതിലെ ആശയങ്ങള് ഈ സിദ്ധാന്തത്തിന്റെ വെളിച്ചത്തില് പഠിക്കുന്നത് എളുപ്പമാണ്. തുടര്ന്നുള്ള വിശദാംശങ്ങള്ക്ക് ഗണസിദ്ധാന്തബോധം ആവശ്യമാണ്.
ക്രമം
order
വാസ്തവിക സംഖ്യകളെ സംബന്ധിച്ച ഒരാശയമാണ് ക്രമം. ഗണങ്ങളെയും 'ക്രമ'പ്പെടുത്താന് കഴിയും. 8-നെക്കാള് ചെറുതാണ് 3 എന്നത് 3 < 8 എന്നും 3 നെക്കാള് വലുതാണ് 8 എന്നത് 8 > 3 എന്നും സൂചിപ്പിക്കപ്പെടുന്നു. സമതയും കൂടി ഉള്പ്പെടുത്തുമ്പോള് ≤, ≥ എന്നീ പ്രതീകങ്ങളാണ് ഉപയോഗിക്കുന്നത്. ഉദാ. a≤b; c≥d; ഇതില് a,b, c, d എന്നിവ വാസ്തവിക സംഖ്യകളാണ്.
നിരപേക്ഷമൂല്യം
Absolute value
പൂര്ണത
Completeness
വാസ്തവിക സംഖ്യാഗണത്തെ ആധാരമാക്കിയാണ് ഇതില് ആശയങ്ങള് പ്രതിപാദിക്കുന്നത്. ഒരു വാസ്തവിക സംഖ്യാഗണ(S)ത്തിലുള്ള ഏത് അംഗത്തിനെക്കാളും വലിയതായി ഒരു വാസ്തവിക സംഖ്യ (b) സ്വീകരിക്കാനുണ്ടെങ്കില്, ആ സംഖ്യ b ആണ്, s ഗണത്തിന്റെ ഒരു b എന്ന ഒരു ഉന്നത പരിബന്ധം (upper bound); S-ലെ ഒരംഗമാകണമെന്നില്ല. ഉദാ. S ={1/8,1/4,1/2}എന്ന ഗണത്തിലെ ഏതു സംഖ്യയും 1-നെക്കാള് ചെറുതാണ്. അതുകൊണ്ട് ട-ന്റെ ഒരു ഉന്നതപരിബന്ധമാണ് 1. S ഗണത്തിനുണ്ടാകാവുന്ന അനവധി പരിബന്ധങ്ങളില്വച്ച് ഏറ്റവും ചെറുതിനെയാണ് അല്പതമ-ഉന്നതപരിബന്ധം (least upper bound:lub ) അഥവാ സുപ്രീമം (Supremum:sup) എന്നു പറയുന്നത്. അതുപോലെ ഏത് അംഗത്തെക്കാളും ചെറുതായ ഒരു വാസ്തവികസംഖ്യയുണ്ടെങ്കില് അതിനെ ഒരു നിമ്നപരിബന്ധം (lower bound) എന്നും അത്തരം പരിബന്ധങ്ങളില് ഏറ്റവും വലിയതിനെ അധികതമ നിമ്നപരിബന്ധം (greatest lower bound:glb) അഥവാ ഇന്ഫിമം (infimum: inf) എന്നും പറയുന്നു.
വാസ്തവികസംഖ്യകളെ നേര്വരയിലെ ബിന്ദുക്കളുമായി അനുയോഗബന്ധത്തില് പ്രതിനിധാനം ചെയ്യാന് കഴിയും. ആ രേഖയെയാണ് വാസ്തവിക സംഖ്യാരേഖയെന്നോ വാസ്തവികരേഖയെന്നോ വാസ്തവികാക്ഷമെന്നോ പറയുന്നത്; R എന്നാണ് ചിഹ്നം. R2 വാസ്തവിക സമതലത്തിലെ എല്ലാ ബിന്ദുക്കളും ചേര്ന്ന ഗണത്തെ സൂചിപ്പിക്കുന്നു.
പൂര്ണതാതത്ത്വം.
ശൂന്യമല്ലാത്ത ഒരു വാസ്തവിക സംഖ്യാഗണമാണ് A എന്നു കരുതുക. R-ന്റെ ഉപഗണമായിരിക്കും A. Rല് A-യ്ക്ക് ഒരു ഉന്നതപരിബന്ധമുണ്ടെങ്കില് R-ല്ത്തന്നെ അതിന് സുപ്രീമവും ഉണ്ടായിരിക്കും. ഇതാണ് പൂര്ണതാതത്ത്വം. R-നെ സംബന്ധിച്ചാണിവിടെ വ്യാഖ്യാനിച്ചതെങ്കിലും മറ്റു ചില സാമാന്യഗണങ്ങള്ക്കും 'പൂര്ണത'യുണ്ട്. R ഒരു പൂര്ണക്രമിക ഫീല്ഡ് (completely ordered field) ആണ്. b ഒരു വാസ്തവിക സംഖ്യയും c ധനവാസ്തവികസംഖ്യയുമാണ് എന്നാണെങ്കില് nc > b ആയിരിക്കുന്നവിധം n എന്നൊരു നിസര്ഗസംഖ്യയുണ്ടായിരിക്കും. ഇതിന് 'ആര്ക്കിമിഡീസ് തത്ത്വ'മെന്നാണ് പറയുന്നത്. അതുപോലെ a, b (a < b) എന്നീ ക്രമത്തിലുള്ള വാസ്തവികസംഖ്യകള്ക്കിടയില് ഒരു ഗണസംഖ്യ (rational number: ആനുപാതികസംഖ്യ)r ഉണ്ടായിരിക്കും. അതായത് a < r < b; ഒന്നുണ്ടെങ്കില് അനന്തം ഗണസംഖ്യകളും ഉണ്ടായിരിക്കും.
ഏകദിഷ്ടഫലനങ്ങള്
( Monotonic functions).
A , B ഇവ ശൂന്യമല്ലാത്ത രണ്ടു വാസ്തവിക സംഖ്യാഗണങ്ങളും f : A → B ഒരു ഫലനവും ആണെന്നു കരുതുക. x1, x2 ഇവ A-യിലെ അംഗങ്ങളും x1 < x2 ഉം ആകുമ്പോഴെല്ലാം f(x1) ≤ f(x2) ആണെങ്കില് f വര്ധമാനഫലനം ആണ് എന്നു പറയുന്നു. , x1, x2 ആകുമ്പോഴെല്ലാം f(x1) ≥ f(x2) ആണെങ്കില് f ഹ്രസ്വമാനഫലനം ആണെന്നും പറയുന്നു. A എന്ന ഗണത്തില് f എന്ന ഫലനം വര്ധമാനമോ അഥവാ ഹ്രസ്വമാനമോ ആണെങ്കില് f ഏകദിഷ്ടമാണ് എന്നു പറയുന്നു.
മിതീയ ഗണങ്ങള്
(Metric Sets).
ദൂരഫലനം അഥവാ മെട്രിക്'
a, b എന്നിവ A എന്ന ഗണത്തിലെ രണ്ടംഗങ്ങളാണെന്നു കരുതുക. d(a, b) എന്ന ചിഹ്നം കൊണ്ടു സൂചിപ്പിക്കപ്പെടുന്നതും a, b എന്നിവയുമായി ബന്ധപ്പെടുത്താവുന്നതുമായ ഒരു വാസ്തവികസംഖ്യ താഴെ ചേര്ക്കുന്ന വ്യവസ്ഥകള്ക്കു വിധേയമാണെങ്കില് d ഒരു മെട്രിക് അഥവാ ദൂരഫലനമാണെന്നു പറയുന്നു; (i) d (a, b) അന്യൂന സംഖ്യയാണ്; അതായത് d(a, b) ≥o.(ii) a-ഉം b-ഉം തുല്യമാണെങ്കില് മാത്രമേ, d(a, b)യുടെ മൂല്യം പൂജ്യം ആകുന്നുള്ളു. (iii) d(a,b)ഉം d(b, a)ഉം തുല്യമാണ്. (iv) a, b, c എന്നിവ A ഗണത്തിലുള്ള അംഗങ്ങളാണെങ്കില്, d(a, b) + d(b, c) ≥ d(a, c). ഇതിനെ ത്രികോണ-അസമത എന്നു പറയുന്നു.
മിതീയഗണം എന്നതുകൊണ്ടുദ്ദേശിക്കുന്നത്, ഒരു ഗണവും (A) അതിനെ ആശ്രയിച്ചിരിക്കുന്ന ഒരു മെട്രിക്കും (d) ചേര്ന്ന ജോടി (A,d) ആണ്. ഇതിന് A എന്നു മാത്രമായിട്ടും പ്രതീകം ഉപയോഗിക്കാറുണ്ട്.
ഉദാ. A {x:x വാസ്തവികസംഖ്യ} A-യിലുള്ള ഏതു അംഗജോടികള് (x1,x2)ക്കും യോജിക്കുന്നവിധം d-യെ നിര്വചിക്കാം. d (x1,x2) = |x1-x2| ഒരു മെട്രിക് ആണ്.
സാമീപ്യങ്ങള്
Neighbourhoods
(A, d) മിതീയഗണമാണെന്നിരിക്കട്ടെ. A-യിലെ ഒരുസ്ഥിരബിന്ദുവും ε ഒരു ധനവാസ്തവിക സംഖ്യയുമാണെന്നു കരുതുക. ഈ വ്യവസ്ഥിതിയില് d(a,x)-ന്റെ മൂല്യം ε-നെക്കാള് ചെറുതായിരിക്കുന്ന വിധത്തിലുള്ള A-യിലെ x അംഗങ്ങള് ചേര്ന്ന ഗണത്തെ a-യുടെ ഒരു സാമീപ്യം എന്നു പറയുന്നു; N(a, ε) എന്നാണിതിന്റെ പ്രതീകം. അതായത് N (a, ε) = {x : x ε A, d (a, x)< ε}. ഈ ഗണത്തില്നിന്ന് a എന്ന ബിന്ദു ഒഴിവാക്കിയാല്, അവശേഷിക്കുന്നത്, N' (a, ε) അപവര്ജിതസാമീപ്യം (deleted neighbourhood) ആണ്.
ആന്തരബിന്ദുക്കളും അതിര്ത്തിബിന്ദുക്കളും
(Interior points and boundary points).
M എന്ന ഗണത്തിന്റെ ഉപഗണമാണ് A എന്നു കരുതുക. ഒരു ഗണ(A)ത്തിലെ അംഗം 'a' ആ ഗണത്തിന്റെ ഒരു 'ആന്തരബിന്ദു'വാകുന്നത്, അതിന്റെ ഏതെങ്കിലും ഒരു സാമീപ്യം N (a, ε) മുഴുവനും അ-ല് ഉള്ക്കൊള്ളുമ്പോഴാണ്; സാമീപ്യം ഒന്നും A-യില് ഉള്ക്കൊള്ളുന്നില്ലെങ്കില് ആ അംഗം 'a' A-യുടെ ഒരു ബഹിര്ബിന്ദു (exterior point) വും ആകും; ഓരോ സാമീപ്യ N(a, ε) വും A യിലെയും A-യ്ക്കു പുറത്തുള്ള ഭാഗത്തെയും അതായത്, M-A യേയും സന്ധിക്കുന്നു (Intersect) എങ്കില് A-യുടെ ഒരു അതിര്ബിന്ദുവാണ് a എന്നു പറയുന്നു. ആന്തരബിന്ദു സമൂഹത്തിന് ആ ഗണത്തിന്റെ ആന്തരഭാഗം (interior) എന്നും ബാഹ്യബിന്ദുക്കളുടെ സമൂഹത്തിന് ആ ഗണത്തിന്റെ ബഹിര്ഭാഗം (exterior) എന്നും പറയുന്നു; അതിര്ബിന്ദുക്കളുടെ സമൂഹം ആ ഗണത്തിന്റെ അതിര്ത്തിഭാഗ(boundary)വും.
അതിര്ത്തിഭാഗവുംകൂടി ഉള്പ്പെടുന്ന ഗണത്തെ സംവൃതഗണം (closed set) എന്നും ആന്തരഭാഗം ഉള്പ്പെടുന്ന ഗണത്തെ വിവൃതഗണം (open set) എന്നും പറയുന്നു.
M എന്ന മിതീയഗണത്തിന്റെ ഒരു ഉപഗണമാണ് A; M-ലുള്ള ഒരു ബിന്ദുവാണ് a. a-യുടെ ഓരോ അപവര്ജിത സാമീപ്യത്തിലും a-യുടെ ഒരു ബിന്ദുവെങ്കിലും ഉണ്ടെങ്കില്, a എന്ന ബിന്ദു A-യുടെ ഒരു സീമാബിന്ദു (limit point) ആണെന്നു പറയുന്നു. ഒരു ഗണത്തിന്റെ എല്ലാ സീമാബിന്ദുക്കളും അതില്ത്തന്നെ ഉള്പ്പെടുന്നുവെങ്കില് ആ ഗണം സംവൃതഗണമാണ്. രണ്ടു ഗണങ്ങള് തമ്മില് പൊതുബിന്ദുവില്ലാതിരിക്കയും ഒന്നു മറ്റൊന്നിന്റെ സീമാബിന്ദുക്കള് ഉള്ക്കൊള്ളാതിരിക്കയുമാണെങ്കില്, അവ വിച്ഛേദിതഗണങ്ങളാണ്. രണ്ടു വിച്ഛേദിതഗണങ്ങളുടെ സംയോഗം (union) ആയി പ്രതിനിധാനം ചെയ്യാന് കഴിയാത്ത ഗണം ബന്ധിത (connected)വും ആണ്.
അനുക്രമങ്ങള്
Sequences
അനുക്രമം നിര്വചിക്കപ്പെടുന്നത് ഒരു ഫലനമായിട്ടാണ്. f : N → M അതായത്, നിസര്ഗസംഖ്യകളെ M എന്ന ഗണത്തിലെ അംഗങ്ങളുമായി ബന്ധപ്പെടുത്തുന്ന ഫലനമാണ് M-ലെ ഒരു അനുക്രമം.
അനുക്രമസീമ
'ബിന്ദുക്കള്' ക്രമമായിരിക്കുമ്പോള് ആ അനുക്രമത്തിന്റെ പ്രവണത നിര്ണയിക്കുന്നതിനുള്ള ആശയമാണ് സീമ. ഒരു സ്ഥിരബിന്ദുവാണ് സീമയെന്നു പറയാം. സാങ്കേതികമായി പറഞ്ഞാല് പരിമേയമായ ഏതാനും അംഗങ്ങളൊഴിച്ച് ശേഷിക്കുന്ന മറ്റു സാന്തമോ അനന്തമോ അംഗങ്ങള് മുഴുവനും ഉള്പ്പെടുന്നതായ ഒരു സാമീപ്യം b എന്ന ഒരു ബിന്ദുവിനുണ്ടെങ്കില്, bയെ അനുക്രമത്തിന്റെ സീമയെന്ന് പറയുന്നു. ഇതിനെ f(n)=b , f(n) = b. എന്ന് എഴുതും.{1,1/2,1/3,...........}. എന്ന അനുക്രമത്തിന്റെ സീമ 0 ആണ്. എന്തുകൊണ്ടെന്നാല് N (0,ε) എന്ന സാമീപ്യത്തില് അതിലെ അനന്തം അംഗങ്ങള് ഉള്പ്പെടുന്നു. ε എന്ന ധനവാസ്തവികസംഖ്യയെ അപേക്ഷിച്ച് N (0,ε) എന്ന ഗണത്തിനു പുറമേ പോകുന്ന അംഗങ്ങളുടെ എണ്ണം പരിമിതമാണ്. സീമ ഉള്ള അനുക്രമത്തെ അഭികേന്ദ്രസരണമെന്നും അല്ലാത്തതിനെ അപകേന്ദ്രസരണമെന്നും പറയുന്നു.
കോഷി അനുക്രമങ്ങള്
അനുക്രമത്തിലെ ഒരു പരിധിക്കുശേഷമുള്ള പദങ്ങളില് ഏതു രണ്ടെണ്ണവും തമ്മിലുള്ള ദൂരം വളരെ ചെറിയ ഒരു ധനവാസ്തവിക സംഖ്യയ്ക്കു താഴെയായിരിക്കുമെങ്കില് ആ അനുക്രമം ഒരു കോഷി അനുക്രമമായിരിക്കും. അഭികേന്ദ്രസരണം ആയ ഏതു അനുക്രമത്തിന്റെയും ഒരു സാമാന്യ സവിശേഷതയാണിത്. എന്നാല് എല്ലാ മിതീയ ഗണങ്ങളിലും കോഷി അനുക്രമങ്ങള് അഭികേന്ദ്രസരണമാകണമെന്നില്ല. വാസ്തവിക സംഖ്യാഅനുക്രമങ്ങളില് കോഷി അനുക്രമങ്ങള് എല്ലാം അഭികേന്ദ്രസരണങ്ങള് ആണ്.
ബോല്സാനോ-വെയര്സ്റ്റ്രോസ് തത്ത്വം
സമതലത്തെ ആസ്പദമാക്കി, അതായത് R2 എന്ന തലത്തെ സംബന്ധിച്ച്, ഈ തത്ത്വം തെളിയിക്കുന്ന മാര്ഗം ഉപയോഗിച്ചു തന്നെ സാമാന്യമായ യൂക്ളിഡിയാതലങ്ങള്ക്കും പ്രയോഗിക്കാവുന്നതാണ്. ഇതിന്റെ പ്രണേതാക്കള് ബോല്സാനോ, വെയര്സ്റ്റ്രോസ് എന്നീ ഗണിതശാസ്ത്രജ്ഞന്മാരാണ്.
Rn-എന്ന n-മാനതലത്തിലെ ഓരോ ബന്ധിത (bounded) അനന്തഗണത്തിനും ഒരു സീമാബിന്ദുവെങ്കിലുമുണ്ട്.
A എന്ന ഗണം ബന്ധിതമായതിനാല് അതുള്ക്കൊള്ളുന്ന ഒരു സംവൃത സമചതുരം (S) കണ്ടെത്താന് കഴിയും. ഈ ചതുരത്തെ നാലു തുല്യ സമചതുരങ്ങളായി തിരിക്കാം (ചിത്രം 2). ഇതില് ഏതെങ്കിലുമൊരു ചതുരത്തിന് (S1), A-യിലെ അനന്തമായ ഭാഗം ഉള്ക്കൊള്ളാന് കഴിയും. A അനന്തമായതിനാല് ഇതു സാധ്യമാണ്. S1-നെ വീണ്ടും നാലു തുല്യഭാഗങ്ങളായി തിരിക്കുക. ഇവയിലൊന്നില് A-യിലെ അനന്തമായ ഭാഗം ഉള്ക്കൊള്ളുന്ന ലഘുചതുരം തുടര്ച്ചയായി കണ്ടെത്തുകയും ചെയ്യാം. അങ്ങനെ S, S1, S2, S3 ... എന്നു ചുരുങ്ങിവരുന്ന ഗണങ്ങളുടെ അനുക്രമം ഉണ്ടാകുന്നു. n വര്ധിപ്പിച്ചുകൊണ്ടു പോയാല് Sn- എന്ന ചതുരത്തിന്റെ വശം ചെറുതായി വരികയും സീമ 0 ആയിത്തീരുകയും ചെയ്യും. S1-ല് നിന്ന് (a1,b1) എന്നൊരു ബിന്ദു, S2-ല് നിന്നു മറ്റൊരു ബിന്ദു (a2, b2), S3-ല് നിന്നു (a3, b3) അങ്ങനെ Sn-ല് നിന്നു (an, bn) (ഈ ബിന്ദുക്കളെല്ലാം വ്യത്യസ്തമാണ്) എന്നിവ ക്രമത്തിലെടുത്താല് അത് ഒരു കോഷി അനുക്രമമായിരിക്കും. Sn-ന്റെ വശത്തിനു സീമ 0 ആയിരിക്കുന്നതാണ് അതിനു കാരണം. അതുകൊണ്ട് (a,b) എന്നൊരു ബിന്ദു R2തലത്തിലുണ്ടാകുന്നു.അതിനുള്ളവ്യവസ്ഥ n സീമ →∞(an,bn), = (a, b) എന്നതാണ്. N ((a, b), ε) എന്ന ഓരോ സാമീപ്യത്തിലും A യിലെ (an,bn) എന്നീ അനന്തം വ്യത്യസ്ത ബിന്ദുക്കള് ഉള്ക്കൊള്ളുന്നതിനാല്, (a, b) എന്ന ബിന്ദു A യുടെ സീമാബിന്ദുവാണ് (ചിത്രം 2).
ഫലനത്തിന്റെ സീമ
A, B എന്നിവ രണ്ടു മിതീയ ഗണങ്ങളായിരിക്കട്ടെ; a, b എന്നിവ A, B ഗണങ്ങളിലെ സ്ഥിരബിന്ദുക്കളും. A ഗണത്തെയോ a ഒഴിവാക്കിക്കൊണ്ടുള്ള A-നെയോ (അതായത് A- {a}), B യിലേക്ക് രൂപാന്തരപ്പെടുത്തുന്ന ഫലനമാണ് f. a ഉള്പെടാത്ത A യുടെ സാമീപ്യത്തെ N' (a, ∂) എന്നു സൂചിപ്പിക്കുക. ∂ ഒരു ധനപൂര്ണസംഖ്യയാണെന്നും N' (a, ∂) ശൂന്യഗണമല്ലെന്നും സങ്കല്പിക്കുക. B-ല് N (b, ε) എന്ന bയുടെ ഓരോ സാമീപ്യത്തിനും അനുയോഗമായി A-ല് N' (a, ∂) എന്നൊരു സാമീപ്യം ഉണ്ടാവുകയും N' (a, ∂) യുടെ രൂപാന്തരണമായ f [N' (a,∂) N (b,ε)-ല് ഉള്ക്കൊള്ളുകയും ആണെങ്കില്, f (x)-ന്റെ സീമ b ആണെന്നു പറയുന്നു; x →af(x)=b എന്നു രേഖപ്പെടുത്താം.
രണ്ടു ഫലനങ്ങളുടെ ആകെത്തുകയുടെയും വ്യത്യാസങ്ങളുടെയും കാര്ത്തീയ ഗുണിതത്തിന്റെയും ഹരണത്തിന്റെയും സീമകള് യഥാക്രമം സീമകളുടെ ആകെത്തുകയും വ്യത്യാസവും ഗുണിതവും ഹരണഫലവുമാണ്; ഹാരകഫലനം ശൂന്യമാകരുതെന്ന നിബന്ധനയുണ്ട്.
അവിച്ഛിന്നത
Continuity
f(x) എന്ന ഫലനം a എന്ന ബിന്ദുവില് അവിച്ഛിന്നമാകണമെങ്കില് f(a)-ക്ക് നിശ്ചിതമായ ഒരു മൂല്യം ഉണ്ടായിരിക്കണം; മാത്രമല്ല, x എന്ന ചരബിന്ദു a എന്ന ബിന്ദുവിനോട് അടുക്കുന്നതനുസരിച്ച് f(x) എന്ന ഫലനം f(a) എന്ന മൂല്യത്തോട് അടുക്കുകയും വേണം. ഇതു കൃത്യതയോടെ ഇപ്രകാരം പറയാം. ε ഒരു ധനസംഖ്യയാണെങ്കില് അതിനു ബന്ധപ്പെട്ട് δഎന്ന ഒരു ധനസംഖ്യ ഉണ്ടായിരിക്കുകയും |x-a | <δആകുമ്പോഴെല്ലാം |f(x) - f(a)| < ε ആകുകയും ചെയ്താല് f(x) എന്ന ഫലനം a-ല് അവിച്ഛിന്നമാണെന്നു പറയും. ഒരു പ്രദേശത്തുള്ള ഓരോ ബിന്ദുവിലും ഒരു ഫലനം അവിച്ഛിന്നമാണെങ്കില് മാത്രമേ ആ പ്രദേശത്തില് ആ ഫലനം അവിച്ഛിന്നം ആണെന്നു പറയാവൂ.
അവിച്ഛിന്നമായ ഒരു ഫലനത്തിന്റെ രണ്ടു മൂല്യങ്ങള്ക്കിടയിലുള്ള ഒരു മൂല്യത്തിന് ചേരുന്നവിധം ആ മൂല്യങ്ങള്ക്ക് ആധാരമായ ബിന്ദുക്കള്ക്കിടയില് ഒരു ബിന്ദു ഉണ്ടായിരിക്കും.
ഏകതാന-അവിച്ഛിന്നത
Uniform continuity
ഫലനത്തിന്റെ സീമയിലും അവിച്ഛിന്നതയിലും സൂചിപ്പിച്ചിരുന്ന ∂,εഎന്നീ ധനവാസ്തവിക സംഖ്യകള് പരസ്പരം ബന്ധപ്പെട്ടിരിക്കുന്നു. എന്നു മാത്രമല്ല ε a എന്ന ബിന്ദുവിനെയും ആശ്രയിച്ചിരിക്കുന്നതാണ് അവിച്ഛിന്നതയില് കാണുന്നത്. എന്നാല് ∂ a എന്ന ബിന്ദുവിനെ ആശ്രയിക്കാതെ തന്നെ ε-നുമായി മാത്രം ബന്ധപ്പെട്ടിരിക്കുകയെന്ന വ്യവസ്ഥയില് അവിച്ഛിന്നതയുണ്ടാകുമ്പോള് അതിന് ഏകതാന-അവിച്ഛിന്നതയെന്നു പറയുന്നു. ഏകതാന-അവിച്ഛിന്നമായ ഫലനം അവിച്ഛിന്നവുമാണ്. ഏകതാന-അവിച്ഛിന്നത അനാലിസിസില് വളരെ പ്രാധാന്യമുള്ള ആശയമാണ്.
വ്യുത്പന്നം
Derivative
R-ല്നിന്നുള്ള ഒരു ഗണത്തെ R-ലേക്കുതന്നെ രൂപാന്തരണം ചെയ്യുന്ന ഫലനമാണ് f എങ്കില് R-ലുള്ള ഓരോ ബിന്ദു (a) വിനും f '(a) എന്നതു നിര്വചിക്കുന്നത് ഇപ്രകാരമാണ്: h പൂജ്യത്തെ സമീപിക്കുന്ന ഒരുചരമാണ്, f(a + h)-ഉം f(a)ഉം തമ്മി ലുള്ള വ്യത്യാസത്തെ h കൊണ്ടു ഹരിച്ചുകിട്ടുന്ന ഫലത്തിന് h പൂജ്യത്തോട് അടുക്കുമ്പോള് സീമയുണ്ടെങ്കില് അതിനു f '(a) എന്നു സൂചിപ്പിക്കുകയും f-ന്റെ a-യിലെ വ്യുത്പന്നമെന്നു വിളിക്കുകയും ചെയ്യുന്നു. അതായത്
h പൂജ്യത്തിലേക്കടുക്കുമ്പോള്, PQ എന്ന ജ്യാവ് (chord)
y = f(x) എന്ന രേഖയ്ക്കു P യിലുള്ള സ്പര്ശകമായി മാറുന്നു. അതുകൊണ്ട് f '(a) എന്നത് ഈ സ്പര്ശകത്തിന്റെ ചരിവുമാനം (slope) ആണ് (ചിത്രം 3).
വ്യുത്പന്നങ്ങളുടെ മാധ്യമൂല്യതത്ത്വം
Mean value theorem
മാധ്യമൂല്യതത്ത്വത്തിന്റെ മുന്നോടിയായി ചില വ്യവസ്ഥകള് ക്കനുസരിച്ച് f എന്ന ഫലനത്തിന്റെ വ്യുത്പന്നം പൂജ്യമാകുന്ന ഘട്ടമാണ് റോള് തത്ത്വത്തില് (Rolle's Theorem) പ്രതിപാദിക്കുന്നത്; (a, b) എന്ന വിവൃതാന്തരാളത്തിലെ ഏത് സാമാന്യബിന്ദുവായ x-നും f '(x) ഉണ്ടായിരിക്കുക; [a b ] എന്ന സംവൃതാന്തരാളത്തില് f അവിച്ഛിന്നമായിരിക്കുക; f(a), f(b) എന്നിവ തുല്യമായിരിക്കുക - ഈ വ്യവസ്ഥിതിയില് f '(z) പൂജ്യമാകുന്ന വിധം (a, b) ല് z എന്നൊരു ബിന്ദുവുണ്ടായിരിക്കും. ഇതാണ് റോള് തത്ത്വം. ഇതിലെ ആദ്യത്തെ രണ്ടു വ്യവസ്ഥകള് മാത്രമായാല്,
f'(z) = f(b)-f(a)/b-a
ആയിരിക്കുന്ന വിധം (a, b) എന്ന വിവൃതാന്തരാളത്തില് ഉള്ക്കൊള്ളുന്ന ഒരു ബിന്ദു (z) ഉണ്ടായിരിക്കും. ഇതാണ് മാധ്യമൂല്യതത്ത്വം. സാമാന്യവത്കരിക്കപ്പെട്ടിട്ടുള്ള ഈ തത്ത്വത്തിന് ധാരാളം വ്യാഖ്യാനങ്ങള് ഉണ്ടായിട്ടുണ്ട്. ഒരു പൊതുതത്ത്വം ഇവിടെ ചേര്ക്കാം. f(x), g(x) എന്നിവ (a, b)-ല് അവകലനക്ഷമവും (അതായത് f '(x), g'(x) ഉണ്ടായിരിക്കുക) a, b എന്നീ ബിന്ദുക്കളില് f അവിച്ഛിന്നവുമാണെങ്കില്, (a, b)-യിലെ ഏതു x-നും g' (x) പൂജ്യമല്ലാത്തിടത്തോളം,
f'(z)/g'(z) =f(b)-f(a)/g(b)-g(a)
ആയിരിക്കുന്നവിധം (a,b)-ല് ഒരു ബിന്ദു (z) ഉണ്ടായിരിക്കും. f(a), g(a) എന്നിവ 0 ആയിരിക്കുമ്പോള്
f'(z) / g'(z) = f(b)/ g (b)
ആയിത്തീരും.
ഇവിടെ a,x എന്നിവയ്ക്കിടയിലാണ് z അതുകൊണ്ട് x a-യിലേക്ക് അടുക്കുമ്പോള് z എന്ന ചരവും aയെ സമീപിക്കുന്നു.
ആംശികാവകലനവും സമ്പൂര്ണാവകലനവും
Partial differentiation and Total differentiation
x,y എന്നീ രണ്ടു സ്വതന്ത്രചരങ്ങളെ ആശ്രയിച്ചിരിക്കുന്ന ഫലനം f R2-ലെ ഒരു വിവൃതഗണമായ A-യെ R-ലേക്കു രൂപാന്തരണം ചെയ്യുന്നുവെന്നു കരുതുക. z = f(x,y). x,y എന്നിവയില് ഏതെങ്കിലും ഒന്നിനെ മാത്രം സ്ഥിരമായി നിര്ത്തി, മറ്റേചരത്തെ ആശ്രയിച്ചു ഫലനമൂല്യത്തിലുണ്ടാകുന്ന വ്യതിയാനത്തിന്റെ സീമ കണ്ടുപിടിക്കാന് കഴിയും. ഈ സീമയാണ് ആംശിക അവകലജാങ്കം (partial differential coefficient).
എന്നു തുടങ്ങിയ ചിഹ്നങ്ങള്കൊണ്ടാണ് ആംശിക അവകലജാങ്കം സൂചിപ്പിക്കുന്നത്. x,y എന്നീ രണ്ടു സ്വതന്ത്രചരങ്ങളുടെ വ്യത്യാസങ്ങളും f(x,y) എന്ന ഫലനത്തെ സ്വാധീനിക്കാം. ആ സ്വാധീനത്തിന്റെ ഒരളവാണ് സമ്പൂര്ണാവകലനം.
സമ്പൂര്ണാവകലനത്തെ ഇങ്ങനെ പ്രകടിപ്പിക്കാം:
df = df(x,y; h, k) = fx(x,y) h + fy (x,y) k അഥവാ
dz = fx (x,y) dx + fy (x, y) dy.
സമാകലനം
Integration
സമാകലനത്തെ അവകലനത്തിന്റെ പ്രതിലോമക്രിയയാണെന്നു പറയാമെങ്കിലും ആകെത്തുക നിര്ണയിക്കുന്ന സമ്പ്രദായത്തില് നിന്നാണ് സമാകലം (Integral) എന്ന ആശയം ഉണ്ടായിട്ടുള്ളത്.
വിഭജനം
[a, b]എന്നത് R-ന്റെ ഒരു സംവൃത-അന്തരാളമാണെന്നു കരുതുക. a = x0, x1, x2, ....x1-1, x1, .....xn = b എന്നീ ബിന്ദുക്കള് [a, b]യെ വിഭജിക്കുന്നു. ഇവിടെ x1-1 നെക്കാള് വലിയതാണ് x1;[a,b], -ല് അവിച്ഛിന്നവും ബന്ധിതവുമാണ് f. m,M, എന്നിവ ക്രമത്തില് [a, b]യുടെ നിമ്നവും ഉന്നതവുമായ പരിധികളാണ് (lower and upper bounds). f([x1-1,x1)-ന്റെ ഇന്ഫിമം ആയ mi (i= 1,2,....n) എല്ലാം m-നും M-നും ഇടയിലായിരിക്കും.m (b-a) ക്കാള് വലുതാണ് S = m1 (x1 -x0) + m2 (x2-x1) +...+mn(xn-xn-1) ഈ സംഖ്യയെക്കാള് വലുതാണ് M (b-a). അതുകൊണ്ട് S ബന്ധിതമാണ്. S-ന്റെ സുപ്രീമംb∫ afdx എന്നു സൂചിപ്പിച്ചാല്, അത് (b-a) [m,M]-ല് ഉള്പ്പെടുന്നു എന്നു സിദ്ധിക്കുന്നു. a,b -യെക്കാള് വലുതാകുമ്പോള് b∫a fdx എന്നത് - a∫bfdxആയും a, bഎന്നിവ തുല്യമാകുമ്പോള് 0 ആയും നിര്വചിക്കപ്പെടാമെങ്കില്, a∫bfdx എന്നതാണ് [a, b] എന്ന സംവൃത അന്തരാളത്തില് f-ന്റെ സ്ഥിരസമാകലം (Definite integral) എന്നു പറയാം.
ഈ സമാകലത്തെ പ്രതിലോമ വ്യുത്പന്നമായി കാണിക്കാന് കഴിയും.F(x) ന്റെ അവകലനമാണ് f(x) എങ്കില് ∫bafdx= F(b)-F(a) ആയിരിക്കും. (ചിത്രം 4).
അനുക്രമങ്ങളും ശ്രേണികളും
നിസര്ഗസംഖ്യാഗണത്തിലുള്ള അംഗങ്ങളെ രൂപാന്തരപ്പെടുത്തുന്ന ഫലനമാണ് അനുക്രമം: അതായത്, a1, a2, .....an,......}. വാസ്തവിക സംഖ്യാഗണ(R)ത്തിലേക്കാണ് രൂപാന്തരണമെങ്കില് ആ അനുക്രമം വാസ്തവികവും, സമ്മിശ്രസംഖ്യാഗണത്തിലേക്കാണെങ്കില് സമ്മിശ്രസംഖ്യാനുക്രമ(complex sequence)വും ആണ്. അനുക്രമത്തെ (Sn) എന്നു സൂചിപ്പിക്കാം.
അഭികേന്ദ്രസരണവും അപകേന്ദ്രസരണവും
(Sn) എന്ന അനുക്രമത്തിലെ ആദ്യത്തെ ഏതാനും ക്ലുപ്തമായ പദങ്ങളൊഴിച്ച് ബാക്കി ക്രമത്തില് ശേഷിക്കുന്നവയെല്ലാം S-ന്റെ ഒരു സാമീപ്യത്തില് ഉള്പ്പെടുമെങ്കില് 'S-ലേക്ക് (Sn) അടുക്കുന്നു' എന്നു പറയാം. സാങ്കേതികമായി പറഞ്ഞാല്, S എന്ന ബിന്ദുവിന്റെ ഒരുസിദ്ധസാമീപ്യമായ N (s, k)-ല് {Sn : n≥ m} ഉള്പ്പെടുന്നവിധം m എന്നൊരു നിസര്ഗസംഖ്യ കണ്ടുപിടിക്കാന് സാധിക്കുമെങ്കില്, (Sn) S-ലേക്ക് അടുക്കുന്നു. ഈ ആശയം n → ∞ Sn = S,എന്നോ ,' Sn → S,എന്നോ പ്രകടിപ്പിക്കാവുന്നതാണ്. n അനന്തമായി തുടര്ന്നുപോകുമ്പോള് സ്ഥിരമായ ഒരു സീമ (S) കല്പിക്കാമെങ്കില്, (Sn) എന്ന അനുക്രമം അഭികേന്ദ്രസരണവും അല്ലാത്തത് അപകേന്ദ്രസരണവും ആണ്. അപകേന്ദ്രസരണത്തില് സീമ Sn എന്നതിനര്ഥമില്ല; അത് അനന്തമാണ്. (Sn ), (tn ) എന്നീ അനുക്രമങ്ങളുടെ സീമകള് ക്രമത്തില് s,t ആണെങ്കില്,
Sn + tn, Sntn, k Sn,Sn/tn(tn≠0)
എന്നിവയുടെ സീമകള് ക്രമത്തില്
S + t, St, kS, t (t ≠0 )
ആയിരിക്കും.∑Sn, അഭികേന്ദ്രസരണമാണെങ്കില് sn-ന്റെ സീമ 0 ആണ്. അഭികേന്ദ്രസരണമാകാനുള്ള വ്യവസ്ഥകള് : (1) ∑Sn ലെ എല്ലാ പദങ്ങളും ധനാത്മകമാണെങ്കില്, ∑Sn ബന്ധിതമായാല് അഭികേന്ദ്രസരണവുമായിരിക്കും; (2) താരതമ്യപരീക്ഷണം (comparison test). ∑bn അഭികേന്ദ്രസരണവും ഒരു പരിധിക്കുശേഷം വരുന്ന പദങ്ങള് തമ്മില് 0 ≤ an ≤ bn എന്ന ബന്ധവുമുണ്ടെങ്കില്, ∑an അഭികേന്ദ്രസരണമായിരിക്കും; (3) ∑| an | അഭികേന്ദ്രസരണമാണെങ്കില് ∑an നിരപേക്ഷ അഭികേന്ദ്രസരണമായിരിക്കും; (4) നിരപേക്ഷ അഭികേന്ദ്രസരണത്തില് അഭികേന്ദ്രസരണം ഉള്ക്കൊള്ളുന്നു; (5) ∑bn അഭികേന്ദ്രസരണം ആണെങ്കില് നിരപേക്ഷ ∑an അഭികേന്ദ്രസരണമാണ്; (6) അംശബന്ധപരീക്ഷണം (Ratio test). ∑an അനുക്രമത്തിന്റെ ഒരു പദവും അതിനു മുമ്പുള്ള പദവും തമ്മിലുള്ള അംശബന്ധത്തിന്റെ കേവലമൂല്യം ഏതെങ്കിലും ഒരു പരിധിക്കുശേഷം ഒരു ധനഭിന്നമാണെങ്കില്, അതായത്
ആണെങ്കില് ∑anനിരപേക്ഷ അഭികേന്ദ്രസരണമാണ്; ഈ അംശബന്ധം 1-നെക്കാള് കൂടുതല് ആണെങ്കില് ∑an അപകേന്ദ്രസരണവുമാണ്.
|an+1/an|നുപകരം അതിന്റെ സീമയെടുത്താലും ഈ നിയമം അനുസരിക്കാവുന്നതാണ്; എന്നാല് സീമയുടെ മൂല്യം ഒന്ന് ആണെങ്കില് പരീക്ഷണം പരാജയപ്പെടുന്നു; (7) സമാകല പരീക്ഷണം (integral test). f ഒരു വാസ്തവിക ഫലനമാണ്; [1,∞) എന്ന ഗണത്തില് അവിച്ഛിന്നവും മൂല്യശോഷണവുമുള്ളതുമാണ്; ധനാത്മകവുമാണ്. an ആയിരിക്കെn ∫1 അഭികേന്ദ്രസരണമാണെങ്കില് മാത്രമേ, ∑an അഭികേന്ദ്രസരണമാകയുള്ളു,
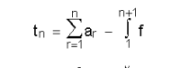
എന്ന സമവാക്യം ഉപയോഗിച്ചാണ് ഇതു തെളിയിക്കുന്നത്;
(8) (-∞ ,1] എന്ന ഗണത്തില് p പെടുന്നെങ്കില്,∑n-p അപകേന്ദ്രസരണവും (1, ∞) ല് പെടുന്നെങ്കില്, അഭികേന്ദ്രസരണവുമാണ്.