This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
അണുകേന്ദ്രവിജ്ഞാനീയം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→ന്യൂക്ളിയാര് പൊട്ടന്ഷ്യല് പ്രാചീരം) |
Mksol (സംവാദം | സംഭാവനകള്) (→അണുകേന്ദ്രസംയോജനം) |
||
| (ഇടക്കുള്ള 19 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 32: | വരി 32: | ||
(12) സെക്ളോട്രോണ് (Cyclotron) എന്ന ഉപകരണം നിര്മിച്ചത് - ലോറന്സ് (1932); | (12) സെക്ളോട്രോണ് (Cyclotron) എന്ന ഉപകരണം നിര്മിച്ചത് - ലോറന്സ് (1932); | ||
| - | (13) ന്യൂട്രോണ് കണ്ടുപിടിച്ചത് - | + | (13) ന്യൂട്രോണ് കണ്ടുപിടിച്ചത് - ചാഡ്വിക് (1932). |
(14) പോസിട്രോണ് കണ്ടുപിടിച്ചത് - ആന്ഡേഴ്സണ് (1932); | (14) പോസിട്രോണ് കണ്ടുപിടിച്ചത് - ആന്ഡേഴ്സണ് (1932); | ||
| വരി 44: | വരി 44: | ||
(18) അണുകേന്ദ്ര ഘടനയെക്കുറിച്ചുള്ള യൌഗിക-അണുകേന്ദ്രസിദ്ധാന്തം നിര്ദേശിച്ചത് - നീല്സ് ബോര് (1936); | (18) അണുകേന്ദ്ര ഘടനയെക്കുറിച്ചുള്ള യൌഗിക-അണുകേന്ദ്രസിദ്ധാന്തം നിര്ദേശിച്ചത് - നീല്സ് ബോര് (1936); | ||
| - | (19) കോസ്മിക കിരണങ്ങളില് മ്യൂ ()- മെസോണ് കണ്ടെത്തിയത് - നെദര്മേയര്, ആന്ഡേഴ്സണ് (1937); | + | (19) കോസ്മിക കിരണങ്ങളില് മ്യൂ (μ)- മെസോണ് കണ്ടെത്തിയത് - നെദര്മേയര്, ആന്ഡേഴ്സണ് (1937); |
(20) അണുകേന്ദ്രകാന്തിക-ആഘൂര്ണത്തെ (Nuclear magnetic moment) കൃത്യമായി നിര്ണയിച്ചത് - റാബി (1938); | (20) അണുകേന്ദ്രകാന്തിക-ആഘൂര്ണത്തെ (Nuclear magnetic moment) കൃത്യമായി നിര്ണയിച്ചത് - റാബി (1938); | ||
| വരി 52: | വരി 52: | ||
(22) ആദ്യത്തെ അണുകേന്ദ്ര റിയാക്റ്റര് നിര്മിച്ചു പ്രവര്ത്തിപ്പിച്ചത് - ഫെര്മി (1942); | (22) ആദ്യത്തെ അണുകേന്ദ്ര റിയാക്റ്റര് നിര്മിച്ചു പ്രവര്ത്തിപ്പിച്ചത് - ഫെര്മി (1942); | ||
| - | (23) പൈ ( ) മെസോണ് എന്ന കണം കണ്ടുപിടിച്ചത് - സെസില് പൌവല്, സീസര് ലാറ്റസ്, ജൂസെപ്പെ | + | (23) പൈ (π) മെസോണ് എന്ന കണം കണ്ടുപിടിച്ചത് - സെസില് പൌവല്, സീസര് ലാറ്റസ്, ജൂസെപ്പെ |
ഒക്കിയാലിനി (1947); | ഒക്കിയാലിനി (1947); | ||
| - | (24) വി (V)-കണത്തിന്റെ കണ്ടുപിടിത്തം - റാച്ചസ്റ്റര് | + | (24) വി (V)-കണത്തിന്റെ കണ്ടുപിടിത്തം - റാച്ചസ്റ്റര് ബട്ലര് (1947); |
(25) പരീക്ഷണശാലയില് കൃത്രിമമായി മെസോണുകള് നിര്മിച്ചത് - ഗാര്ഡ്നര്, ലാറ്റസ് (1948); | (25) പരീക്ഷണശാലയില് കൃത്രിമമായി മെസോണുകള് നിര്മിച്ചത് - ഗാര്ഡ്നര്, ലാറ്റസ് (1948); | ||
| വരി 69: | വരി 69: | ||
ഒരു അണുകേന്ദ്രത്തില് m<sub>p</sub> ദ്രവ്യമാനം വീതമുള്ള z പ്രോട്ടോണുകളും M<sub>n</sub> വീതമുള്ള N ന്യൂട്രോണുകളും അടങ്ങിയിരിക്കുന്നു. Z പ്രോട്ടോണുകളുടെ ആകെ ദ്രവ്യമാനം Z ഹൈഡ്രജന് അണുകേന്ദ്രങ്ങളുടേതായിരിക്കും. അതിനാല് അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനം M=M<sub>H</sub> Z+M<sub>n</sub>(A-Z) ആകേണ്ടതാണ്.[[Image:pno.339dr.png|thumb|left|വിവിധ ന്യൂക്ലിയസ്സുകളുടെ ശരാശരി ബന്ധന ഊര്ജ്ജം]] | ഒരു അണുകേന്ദ്രത്തില് m<sub>p</sub> ദ്രവ്യമാനം വീതമുള്ള z പ്രോട്ടോണുകളും M<sub>n</sub> വീതമുള്ള N ന്യൂട്രോണുകളും അടങ്ങിയിരിക്കുന്നു. Z പ്രോട്ടോണുകളുടെ ആകെ ദ്രവ്യമാനം Z ഹൈഡ്രജന് അണുകേന്ദ്രങ്ങളുടേതായിരിക്കും. അതിനാല് അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനം M=M<sub>H</sub> Z+M<sub>n</sub>(A-Z) ആകേണ്ടതാണ്.[[Image:pno.339dr.png|thumb|left|വിവിധ ന്യൂക്ലിയസ്സുകളുടെ ശരാശരി ബന്ധന ഊര്ജ്ജം]] | ||
| - | ഇവിടെ M<sub>H</sub> ഹൈഡ്രജന് അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനവും A=Z+N- ആണ്. എന്നാല് അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനം (M) മേല്പറഞ്ഞതില് കുറവായിരിക്കും. ദ്രവ്യമാനവ്യത്യാസം, M<sub>H</sub>Z+M<sub>n</sub>(A-Z)-M= Δ അതായത് Δ ദ്രവ്യനഷ്ടം സംഭവിക്കുന്നു. പ്രോട്ടോണുകളേയും ന്യൂട്രോണുകളേയും അതായത് ന്യൂക്ളിയോണുകളെ ബന്ധിക്കുന്ന ഊര്ജമാണിത്. അതിനാല് ബന്ധന-ഊര്ജം B=Δc<sup>2</sup>={M<sub>H</sub>Z+M<sub>n</sub>(A-Z)-M}C<sup>2</sup>.ജൂള്സ്,e.v.എന്ന് ഇലക്ട്രോണ് വോള്ട്ടായും ഇത് കണക്കാക്കപ്പെടുന്നു. (c-പ്രകാശവേഗം). ഓരോ ന്യൂക്ലിയോണിനെയും ബന്ധിക്കുന്ന ശ.ശ. ഊര്ജം B=<math>\frac{[M_HZ+M_n(A-Z)-M]C^2}{A}</math> ഇത് അണുകേന്ദ്രബലങ്ങളെ എതിര്ത്ത് ഓരോ ന്യൂക്ളിയോണിനെയും വേര്പെടുത്തി ദൂരെ മാറ്റുവാന് വേണ്ടിവരുന്ന പ്രവൃത്തിയെ ആണ് സൂചിപ്പിക്കുന്നത്. A-യെ അപേക്ഷിച്ച് B എപ്രകാരം മാറിവരുന്നു എന്നു ചിത്രത്തില്നിന്നു മനസ്സിലാക്കാം. ഏറ്റവും സ്ഥിരമായ അണുസമഭാരികം (isobar) (നോ: അണു) ആണ് കണക്കിലെടുത്തിട്ടുള്ളത്. A-50-നോടു സമീപിക്കുമ്പോള് B = 8.4 MeV കുറയുന്നില്ല. ചെറുതും വലുതും ദ്രവ്യമാനസംഖ്യയുള്ള അണുക്കള്ക്കു B ഇതിനേക്കാള് കുറവാണ്. വളരെ ചെറിയ ദ്രവ്യമാനസംഖ്യയുള്ള അണുക്കളുടെ | + | ഇവിടെ M<sub>H</sub> ഹൈഡ്രജന് അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനവും A=Z+N- ആണ്. എന്നാല് അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനം (M) മേല്പറഞ്ഞതില് കുറവായിരിക്കും. ദ്രവ്യമാനവ്യത്യാസം, M<sub>H</sub>Z+M<sub>n</sub>(A-Z)-M= Δ അതായത് Δ ദ്രവ്യനഷ്ടം സംഭവിക്കുന്നു. പ്രോട്ടോണുകളേയും ന്യൂട്രോണുകളേയും അതായത് ന്യൂക്ളിയോണുകളെ ബന്ധിക്കുന്ന ഊര്ജമാണിത്. അതിനാല് ബന്ധന-ഊര്ജം B=Δc<sup>2</sup>={M<sub>H</sub>Z+M<sub>n</sub>(A-Z)-M}C<sup>2</sup>.ജൂള്സ്,e.v.എന്ന് ഇലക്ട്രോണ് വോള്ട്ടായും ഇത് കണക്കാക്കപ്പെടുന്നു. (c-പ്രകാശവേഗം). ഓരോ ന്യൂക്ലിയോണിനെയും ബന്ധിക്കുന്ന ശ.ശ. ഊര്ജം B=<math>\frac{[M_HZ+M_n(A-Z)-M]C^2}{A}</math> ഇത് അണുകേന്ദ്രബലങ്ങളെ എതിര്ത്ത് ഓരോ ന്യൂക്ളിയോണിനെയും വേര്പെടുത്തി ദൂരെ മാറ്റുവാന് വേണ്ടിവരുന്ന പ്രവൃത്തിയെ ആണ് സൂചിപ്പിക്കുന്നത്. A-യെ അപേക്ഷിച്ച് B എപ്രകാരം മാറിവരുന്നു എന്നു ചിത്രത്തില്നിന്നു മനസ്സിലാക്കാം. ഏറ്റവും സ്ഥിരമായ അണുസമഭാരികം (isobar) (നോ: അണു) ആണ് കണക്കിലെടുത്തിട്ടുള്ളത്. A-50-നോടു സമീപിക്കുമ്പോള് B = 8.4 MeV കുറയുന്നില്ല. ചെറുതും വലുതും ദ്രവ്യമാനസംഖ്യയുള്ള അണുക്കള്ക്കു B ഇതിനേക്കാള് കുറവാണ്. വളരെ ചെറിയ ദ്രവ്യമാനസംഖ്യയുള്ള അണുക്കളുടെ B-ല് മുറതെറ്റിയ വ്യതിയാനമാണ് കാണുന്നത്. ഒരു ന്യൂക്ളിയോണിന്റെ ബന്ധന ഊര്ജം <math>\frac{B}{A}</math> ആണ്. |
== സ്വച്ഛന്ദ-അണുകേന്ദ്ര വിഘടനം == | == സ്വച്ഛന്ദ-അണുകേന്ദ്ര വിഘടനം == | ||
| - | + | Spontaneous disintegration of the nucleus | |
| - | അണുഭാരം വളരെ കൂടുതലുള്ള മൂലകങ്ങള് വികിരണത്തിനു (radiation) സ്വയം വിധേയമായി ഒന്നിനുപുറകെ മറ്റൊന്ന് എന്ന ക്രമത്തില് വിവിധ മൂലകങ്ങളായി രൂപം പ്രാപിച്ച് ഒടുവില് സ്ഥിരമൂലകമായ ഈയ (lead)ത്തില് എത്തിനില്ക്കുന്ന ഒരു പ്രത്യേകത പ്രദര്ശിപ്പിക്കുന്നുണ്ട്. സ്വാഭാവിക റേഡിയോആക്റ്റിവത (natural radioactivity) എന്നറിയപ്പെടുന്ന പ്രതിഭാസമാണിത്. ആല്ഫാ, ബീറ്റാ, ഗാമാ (αβγ ) എന്നീ മൂന്നുതരം രശ്മികളാണ് വികിരണം ചെയ്യപ്പെടുന്നത്. ആല്ഫാ രശ്മികളായി പുറപ്പെടുന്നത് ഹീലിയം അണുകേന്ദ്രങ്ങള് തന്നെയാണ്. അവയ്ക്കു നിശ്ചിതതോതില് ഊര്ജവും ഇലക്ട്രോണിന്റെ രണ്ടിരട്ടി ധനചാര്ജുമുണ്ട്. ബീറ്റ രശ്മികളായി വരുന്നത് ഇലക്ട്രോണുകള് തന്നെയാണ്. അവയ്ക്ക് അവിച്ഛിന്ന-ഊര്ജ സ്പെക്ട്രം ( | + | അണുഭാരം വളരെ കൂടുതലുള്ള മൂലകങ്ങള് വികിരണത്തിനു (radiation) സ്വയം വിധേയമായി ഒന്നിനുപുറകെ മറ്റൊന്ന് എന്ന ക്രമത്തില് വിവിധ മൂലകങ്ങളായി രൂപം പ്രാപിച്ച് ഒടുവില് സ്ഥിരമൂലകമായ ഈയ (lead)ത്തില് എത്തിനില്ക്കുന്ന ഒരു പ്രത്യേകത പ്രദര്ശിപ്പിക്കുന്നുണ്ട്. സ്വാഭാവിക റേഡിയോആക്റ്റിവത (natural radioactivity) എന്നറിയപ്പെടുന്ന പ്രതിഭാസമാണിത്. ആല്ഫാ, ബീറ്റാ, ഗാമാ (α,β,γ) എന്നീ മൂന്നുതരം രശ്മികളാണ് വികിരണം ചെയ്യപ്പെടുന്നത്. ആല്ഫാ രശ്മികളായി പുറപ്പെടുന്നത് ഹീലിയം അണുകേന്ദ്രങ്ങള് തന്നെയാണ്. അവയ്ക്കു നിശ്ചിതതോതില് ഊര്ജവും ഇലക്ട്രോണിന്റെ രണ്ടിരട്ടി ധനചാര്ജുമുണ്ട്. ബീറ്റ രശ്മികളായി വരുന്നത് ഇലക്ട്രോണുകള് തന്നെയാണ്. അവയ്ക്ക് അവിച്ഛിന്ന-ഊര്ജ സ്പെക്ട്രം (continuous energy spectrum) ആണുള്ളത്. ഗാമാ ( γ)-രശ്മികള് എക്സ്-രശ്മികളെ(X-rays)ക്കാള് തരംഗനീളം കുറഞ്ഞ വിദ്യുത് കാന്തിക തരംഗങ്ങളാണ്. അവയുടെ ഊര്ജത്തിനു ചില നിശ്ചിതമായ അളവുകളുണ്ട്. അറിവില്പ്പെട്ട എല്ലാ റേഡിയോ ആക്റ്റിവ് രൂപാന്തരണങ്ങളിലും (Radioactive transformations) α അല്ലെങ്കില് β കണമാണ് ഉത്സര്ജിതമാകുന്നത്; ഒരു രൂപാന്തരണത്തില് ഏതെങ്കിലുമൊന്നുമാത്രം. A ദ്രവ്യമാനസംഖ്യയും Z അണുസംഖ്യയുമുള്ള ഒരു അണു α -കണത്തെ ഉത്സര്ജനം ചെയ്യുമ്പോള് നൂതനമായുണ്ടാകുന്ന അണുവിന്റെ ദ്രവ്യമാനസംഖ്യ (A-4)-ഉം അണുസംഖ്യ (Z- 2)-ഉം ആണ്. ഒരു β-കണമാണ് ഉത്സര്ജിതമാകുന്നതെങ്കില് പുതിയ അണുവിന്റെ ദ്രവ്യമാനസംഖ്യ A തന്നെയാണ്; അണുസംഖ്യ (Z + 1) ആകുകയും ചെയ്യും. ഇലക്ട്രോണിന്റെ ദ്രവ്യമാനം തുച്ഛമാണെന്നതാണ് ഇതിനു കാരണം. β-കണം ഉത്സര്ജിതമാകുമ്പോള് അണുകേന്ദ്രത്തിലെ ഒരു ന്യൂട്രോണ്, പ്രോട്ടോണ് ആയിത്തീര്ന്ന്, മൊത്തം ധനചാര്ജ് (Z + 1) ആയിത്തീരുന്നു. |
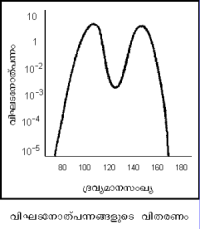
[[Image:PP3340.png|thumb|βകണങ്ങളുടെ ഊര്ജ വിതരണം]] | [[Image:PP3340.png|thumb|βകണങ്ങളുടെ ഊര്ജ വിതരണം]] | ||
| വരി 83: | വരി 83: | ||
Nuclear Pontential barrier | Nuclear Pontential barrier | ||
| - | യുറേനിയം അണുകേന്ദ്രം α-കണങ്ങളെ പ്രകീര്ണനം ചെയ്യുമ്പോള് ശ്രദ്ധേയമായ ചില വസ്തുതകള് വെളിപ്പെടുന്നു. തോറിയം-C<sup>1</sup>-ല് (Th-C<sup>1</sup>) നിന്നു ലഭിക്കുന്ന 9 MeV ഊര്ജമുള്ളവ കൂളൂംനിയമത്തെ അതിലംഘിച്ച് യുറേനിയം അണുകേന്ദ്രത്തെ സമീപിക്കുന്നതിനു ശക്തിയുള്ളതല്ല, അണുകേന്ദ്രത്തില്നിന്നു 3 x 10<sup>-12</sup> സെ.മീ. ദൂരം വരെയെങ്കിലും അണുകേന്ദ്രമണ്ഡലത്തില് α-കണത്തിന്റെ സ്ഥാനികോര്ജം (Pontential energy) കൂളും നിയമത്തിന് | + | യുറേനിയം അണുകേന്ദ്രം α-കണങ്ങളെ പ്രകീര്ണനം ചെയ്യുമ്പോള് ശ്രദ്ധേയമായ ചില വസ്തുതകള് വെളിപ്പെടുന്നു. തോറിയം-C<sup>1</sup>-ല് (Th-C<sup>1</sup>) നിന്നു ലഭിക്കുന്ന 9 MeV ഊര്ജമുള്ളവ കൂളൂംനിയമത്തെ അതിലംഘിച്ച് യുറേനിയം അണുകേന്ദ്രത്തെ സമീപിക്കുന്നതിനു ശക്തിയുള്ളതല്ല, അണുകേന്ദ്രത്തില്നിന്നു 3 x 10<sup>-12</sup> സെ.മീ. ദൂരം വരെയെങ്കിലും അണുകേന്ദ്രമണ്ഡലത്തില് α-കണത്തിന്റെ സ്ഥാനികോര്ജം (Pontential energy) കൂളും നിയമത്തിന് (Ur=<math>\frac{2 Ze^2}{r}</math>) വിധേയമാണ്. |
'''α-ന്യൂക്ലിയര് പൊട്ടന്ഷ്യല് പ്രാചീരം''' | '''α-ന്യൂക്ലിയര് പൊട്ടന്ഷ്യല് പ്രാചീരം''' | ||
[[Image:pEo341.png|left]] | [[Image:pEo341.png|left]] | ||
| - | യുറേനിയം അണുകേന്ദ്രത്തെ സമീപിക്കുന്ന ഒരു α-കണം അഭിമുഖീകരിക്കുന്നത് 9 Mev സ്തരമുള്ള ഒരു പൊട്ടന്ഷിയ ഊര്ജപ്രാചീരമാണ്. എന്നാല് യുറേനിയം അണുകേന്ദ്രം വമിക്കുന്ന α-കണത്തിനു 4 Mev ഊര്ജമാണുള്ളത്. അകത്തും ഈ ഊര്ജംതന്നെയാണുണ്ടായിരിക്കേണ്ടത്. ഈ α-കണത്തിന് ഒരു തരംഗസ്വരൂപം കൂടിയുള്ളതുകൊണ്ടാണ് 4 MeV ഉള്ള α-കണം 9 MeV സ്തരത്തിലുള്ള പ്രാചീരം കടന്നു പുറത്തുവരുന്നത്. അതിന്റെ തരംഗനീളം ആണ് h | + | അണുകേന്ദ്രത്തില്നിന്നുള്ള ദൂരം (r) 3 x 10<sup>-12</sup> സെ.മീ. ആണെങ്കില് സ്ഥാനികോര്ജം 9 MeVആയിരിക്കും. ദൂരംകുറയുംതോറും സ്ഥാനികോര്ജം വര്ധിച്ച് അധികതമത്തിലെത്തിക്കഴിഞ്ഞാല് പിന്നെ കൂളൂംനിയമം തകര്ന്നുപോകുന്നു. ഈ വികര്ഷണക്ഷമത (repulsive potential) α-കണത്തിന് അണുകേന്ദ്രത്തില് പ്രവേശനം നിരോധിക്കുന്നു. അത് ഒരു പൊട്ടന്ഷിയ പ്രാചീരമായി കണക്കാക്കാവുന്നതാണ്. അണുകേന്ദ്രത്തില്നിന്നും പുറത്തുവരുന്നതിനുമുമ്പ് അല്പസമയമെങ്കിലും α-കണം ആ രൂപത്തില് അണുകേന്ദ്രത്തില് ഉണ്ടായിരിക്കണം. അപ്പോള് α-കണവും റേഡിയോ ആക്റ്റിവ് അണുകേന്ദ്രവും തമ്മില് അകത്തും പുറത്തും ഉണ്ടാകുന്ന പരസ്പരക്രിയ (interaction) ആണ് ചിത്രത്തില് കാണിച്ചിട്ടുള്ള സ്ഥാനികോര്ജലേഖ(potential energy curve) സൂചിപ്പിക്കുന്നത്. r<sub>2</sub> മുതല് r<sub>1</sub> വരെ ലേഖ ഉയര്ന്നുകൊണ്ടിരിക്കുന്ന ഭാഗം α-കണം അണുകേന്ദ്രത്തെ സമീപിക്കുമ്പോള് വര്ധിച്ചുവരുന്ന വികര്ഷണത്തെ കാണിക്കുന്നു. അണുകേന്ദ്രത്തിന്റെ അകത്തും സമീപത്തും ഈ ലേഖയുടെ ആകൃതി കൃത്യമായി മനസ്സിലാക്കാന് കഴിഞ്ഞിട്ടില്ല. എന്നാല് വികര്ഷണക്ഷമതയ്ക്കുപകരം ഒരു ആകര്ഷണക്ഷമത V<sub>0</sub>, r<sub>0</sub> എന്ന ദൂരംവരെ പ്രവര്ത്തിക്കുന്നു. ഈ ദൂരമാണ് അണുകേന്ദ്രത്തിന്റെ ഫലപ്രദമായ വ്യാസാര്ധം. α-കണം പുറത്തുവരുമ്പോള് അതിനുള്ള ഊര്ജം (E<sub>α</sub>) തന്നെയാണ് അതിനകത്തുമുള്ളത്. α-കണത്തിന്റെ ഗതികോര്ജമായി അവശേഷിക്കുന്നത് ആകെയുള്ള E<sub>α</sub>-യില്നിന്നു V<sub>0</sub> കുറച്ചുകിട്ടുന്ന E<sub>α</sub>-V<sub>0</sub> ആണ്. |
| + | |||
| + | |||
| + | യുറേനിയം അണുകേന്ദ്രത്തെ സമീപിക്കുന്ന ഒരു α-കണം അഭിമുഖീകരിക്കുന്നത് 9 Mev സ്തരമുള്ള ഒരു പൊട്ടന്ഷിയ ഊര്ജപ്രാചീരമാണ്. എന്നാല് യുറേനിയം അണുകേന്ദ്രം വമിക്കുന്ന α-കണത്തിനു 4 Mev ഊര്ജമാണുള്ളത്. അകത്തും ഈ ഊര്ജംതന്നെയാണുണ്ടായിരിക്കേണ്ടത്. ഈ α-കണത്തിന് ഒരു തരംഗസ്വരൂപം കൂടിയുള്ളതുകൊണ്ടാണ് 4 MeV ഉള്ള α-കണം 9 MeV സ്തരത്തിലുള്ള പ്രാചീരം കടന്നു പുറത്തുവരുന്നത്. അതിന്റെ തരംഗനീളം ആണ് h <math>\sqrt {2m(E-V)}</math>. ഇവിടെ, E ചിത്രത്തില് P A B നിരപ്പായി കാണിച്ചിട്ടുള്ള ആകെ ഊര്ജവും V സ്ഥിതികോര്ജവുമാണ്. കണം MBAC DC' A' B' M' രേഖയ്ക്കു മുകളിലാണ്; അതായത് പൊട്ടന്ഷ്യല് വെല്ലി(potential well)നകത്തോ പുറത്തോ ആയിരിക്കണം. Aa,Bb,aA'a',B'b' എന്നീ പരിധികള്ക്കകത്ത് E-യെക്കാള് കൂടുതലാണ് V. അപ്പോള് E-V ഋണാത്മകമാകയാല് തരംഗനീളം കല്പിതസംഖ്യ (imaginary number) ആയിരിക്കുന്നു. അതിന്റെ അര്ഥം തരംഗത്തിനു AC DC' A' എന്ന അതിര്ത്തിക്കുള്ളില് പൂര്ണപ്രതിഫലനം (total reflection) സംഭവിക്കുന്നു എന്നതാണ്. അണുവില് ഇലക്ട്രോണുകള് നിശ്ചിത ഊര്ജങ്ങളിലും ആവൃത്തി(frequency)കളിലും സ്ഥിതി ചെയ്യുന്നതുപോലെ അണുകേന്ദ്രത്തിനകത്ത് α-കണങ്ങള് ചില നിശ്ചിത ഊര്ജങ്ങളിലും ആവൃത്തികളിലും സ്ഥിതിചെയ്യുന്നുണ്ടാകണം. ചിത്രത്തില് AB,A'B' എന്നീ മേഖലകളില് തരംഗനീളം കല്പിതമാണെങ്കിലും തരംഗഫലനം (wave function) ψ=ψ<sub>0</sub>sin 2πrt വാസ്തവികം (real) ആണ്. തരംഗ-ആയാമം (wave amplitude) A-യിലോ A'-ലോ ശൂന്യമാകുന്നില്ലെങ്കിലും എക്സ്പൊണന്ഷ്യല് (exponential) ആയി കുറഞ്ഞ് B-യില് അഥവാ B'-ല് എത്തുമ്പോള് തുച്ഛമാകുന്നു എന്നല്ലാതെ പൂജ്യമാകുന്നില്ല. B അഥവാ B' തരണംചെയ്താല് തരംഗം വീണ്ടും വാസ്തവികമായിത്തീരുന്നു. ആയാമം കുറവുള്ള ഒരു തരംഗം അണുകേന്ദ്രത്തില്നിന്നു പുറത്ത് <math>\frac{h}\sqrt{2 mE}</math> തരംഗനീളമുള്ള ഒരു ഗോളീയ തരംഗം (spherical wave) ജനിക്കുന്നു. ഒരു തരംഗം അണുകേന്ദ്രത്തിനകത്തുള്ള ഒരു തരംഗം ക്രമേണ ക്ഷയിക്കുന്നുവെന്നര്ഥം. α-കണം അണുകേന്ദ്രത്തില്നിന്നു രക്ഷപ്പെടാനുള്ള സാധ്യതയുണ്ടാകുന്നു. | ||
പ്രാചീരത്തിന്റെ ഉയരം കൂടുന്തോറും തരംഗസമൂഹം (wave packet) പുറത്തേക്ക് ഒഴുകുന്ന നിരക്കു ചുരുങ്ങുകയും അണുകേന്ദ്രത്തില്നിന്നു പുറത്തുവരുവാനുള്ള സാധ്യത കുറയുകയും ചെയ്യും. | പ്രാചീരത്തിന്റെ ഉയരം കൂടുന്തോറും തരംഗസമൂഹം (wave packet) പുറത്തേക്ക് ഒഴുകുന്ന നിരക്കു ചുരുങ്ങുകയും അണുകേന്ദ്രത്തില്നിന്നു പുറത്തുവരുവാനുള്ള സാധ്യത കുറയുകയും ചെയ്യും. | ||
| വരി 102: | വരി 105: | ||
ഒരു തുള്ളിക്കകത്തുള്ള തന്മാത്രകള് അവയുടെ ഏറ്റവും സമീപത്തുള്ള തന്മാത്രകളുടെ സ്വാധീനശക്തിക്കു മാത്രമേ വിധേയമായിരിക്കയുള്ളു. അതുപോലെ ന്യൂക്ളിയോണും ന്യൂക്ളിയോണും തമ്മിലുള്ള ബലങ്ങള്ക്കു ഹ്രസ്വപരാസമേയുള്ളു. തുള്ളിയുടെ പ്രതലത്തിലുള്ള തന്മാത്രകള് അകത്തുള്ളവയെപ്പോലെ ദൃഢമായ ബന്ധനത്തില് അല്ല സ്ഥിതിചെയ്യുന്നത്. അതുപോലെ അണുകേന്ദ്രത്തിന്റെ പ്രതലത്തിലെ ന്യൂക്ളിയോണുകള് അകത്തുള്ളവയെപ്പോലെ ദൃഢമായി ബന്ധപ്പെട്ടിരിക്കുന്നില്ല. | ഒരു തുള്ളിക്കകത്തുള്ള തന്മാത്രകള് അവയുടെ ഏറ്റവും സമീപത്തുള്ള തന്മാത്രകളുടെ സ്വാധീനശക്തിക്കു മാത്രമേ വിധേയമായിരിക്കയുള്ളു. അതുപോലെ ന്യൂക്ളിയോണും ന്യൂക്ളിയോണും തമ്മിലുള്ള ബലങ്ങള്ക്കു ഹ്രസ്വപരാസമേയുള്ളു. തുള്ളിയുടെ പ്രതലത്തിലുള്ള തന്മാത്രകള് അകത്തുള്ളവയെപ്പോലെ ദൃഢമായ ബന്ധനത്തില് അല്ല സ്ഥിതിചെയ്യുന്നത്. അതുപോലെ അണുകേന്ദ്രത്തിന്റെ പ്രതലത്തിലെ ന്യൂക്ളിയോണുകള് അകത്തുള്ളവയെപ്പോലെ ദൃഢമായി ബന്ധപ്പെട്ടിരിക്കുന്നില്ല. | ||
| - | ഈ ആശയങ്ങളെല്ലാം കണക്കിലെടുത്ത് A,Z,M എന്നീ ഭൌതികവസ്തുതകള് (Physical data) ഉള്പ്പെടുത്തി <sup>A</sup>M<sub>z</sub> എന്ന അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനത്തെയും E<sub>B</sub> എന്ന ബന്ധനോര്ജ(binding energy)ത്തെയും ചേര്ത്തുള്ള ഒരു ആനുഭവികസൂത്രവാക്യം (empirical formula) രൂപപ്പെടുത്താന് സാധിച്ചു: <sup>A</sup>M<sub>z</sub>=Z M<sub>H</sub>+(A-Z)M<sub>n</sub>-E<sub>B</sub>. ഇവിടെ M<sub>H</sub>,M<sub>n</sub> എന്നിവ ക്രമത്തില് ഒരു ഹൈഡ്രജന് അണുവിന്റെയും ന്യൂട്രോണിന്റെയും ദ്രവ്യമാനമാണ്. അണുദ്രവ്യത്തെയും ബന്ധനോര്ജത്തെയും വളരെ സൂക്ഷ്മതയോടെ കണക്കാക്കിയെടുക്കാന് ഈ പരിഗണനയിലൂടെ സാധിക്കുന്നു. ഇതിനുപുറമേ | + | ഈ ആശയങ്ങളെല്ലാം കണക്കിലെടുത്ത് A,Z,M എന്നീ ഭൌതികവസ്തുതകള് (Physical data) ഉള്പ്പെടുത്തി <sup>A</sup>M<sub>z</sub> എന്ന അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനത്തെയും E<sub>B</sub> എന്ന ബന്ധനോര്ജ(binding energy)ത്തെയും ചേര്ത്തുള്ള ഒരു ആനുഭവികസൂത്രവാക്യം (empirical formula) രൂപപ്പെടുത്താന് സാധിച്ചു: <sup>A</sup>M<sub>z</sub>=Z M<sub>H</sub>+(A-Z)M<sub>n</sub>-E<sub>B</sub>. ഇവിടെ M<sub>H</sub>,M<sub>n</sub> എന്നിവ ക്രമത്തില് ഒരു ഹൈഡ്രജന് അണുവിന്റെയും ന്യൂട്രോണിന്റെയും ദ്രവ്യമാനമാണ്. അണുദ്രവ്യത്തെയും ബന്ധനോര്ജത്തെയും വളരെ സൂക്ഷ്മതയോടെ കണക്കാക്കിയെടുക്കാന് ഈ പരിഗണനയിലൂടെ സാധിക്കുന്നു. ഇതിനുപുറമേ <sup>238</sup>U<sub>92</sub> എന്ന അണു ഒരു α-ഉത്സര്ജകമാണെന്നുംβ-ഉത്സര്ജകമല്ലെന്നും സ്ഥാപിക്കാന് കഴിയും. ഉത്സര്ജനത്തിന്റെ ഊര്ജവും കണക്കാക്കാന് കഴിയുന്നു. ഒരു അണുകേന്ദ്രത്തിന്റെ വിഘടനാഭികഗുണങ്ങളെക്കുറിച്ചു പ്രവചിക്കാന് കഴിയുമെന്ന് ഇതില്നിന്നു മനസ്സിലാക്കാം. എങ്ങനെ അണുകേന്ദ്രവിഘടനം (nuclear fission) സംഭവിക്കുമെന്നു വിശദീകരിക്കുന്നതിലാണ് ദ്രാവകത്തുള്ളി മാതൃക വിജയിക്കുന്നത്. മന്ദഗതിയിലുള്ള ന്യൂട്രോണുകള് കൊണ്ട് <sup>235</sup>U<sub>92</sub> അണുവിന് വിഘടനം സംഭവിക്കുമെന്നും <sup>238</sup>U<sub>92</sub> അണുവിന് അതു സംഭവിക്കണമെങ്കില് അതിവേഗം ചലിക്കുന്ന ന്യൂട്രോണുകള് ആവശ്യമാണെന്നും സ്ഥാപിക്കാന് കഴിയും. ബന്ധനോര്ജസൂത്രം (binding energy formula) ഉപയോഗിച്ച് എല്ലാ അണുകേന്ദ്രങ്ങളുടെയും ബന്ധനോര്ജം (E<sub>B</sub>) കണ്ടുപിടിക്കാം. Z-നെ അപേക്ഷിച്ച് E<sub>B</sub> ഏതുപ്രകാരം പരിവര്ത്തിതമാകുന്നുവെന്ന് ലേഖ (curve) വരച്ച് അതില്നിന്നു മനസ്സിലാക്കാം. അതില്നിന്ന് അണുകേന്ദ്രങ്ങളുടെ സ്ഥിരത്വഗുണങ്ങളെ (stability properties)ക്കുറിച്ചും പ്രത്യേക സമഭാരിക (isobar) അണുക്കളുടെ βആക്റ്റിവതയെക്കുറിച്ചും അറിവുലഭിക്കുന്നതാണ്. |
=== അണുകേന്ദ്ര കവചമാതൃക === | === അണുകേന്ദ്ര കവചമാതൃക === | ||
| വരി 111: | വരി 114: | ||
[[Image:p342.png]] | [[Image:p342.png]] | ||
| - | എന്നാല് ഓരോ | + | എന്നാല് ഓരോ ന്യൂക്ലിയോണിനും <math>\frac{1}{2}</math> <math>\frac{h}{2\pi} |
| + | </math> എന്ന ചക്രണകോണീയസംവേഗവും (spin angular momentum), lh/2 എന്ന കക്ഷീയ കോണീയസംവേഗവും (axial angular momentum) കല്പിക്കുകയാണെങ്കില് കോണീയസംവേഗം (l±1/2) h/2π =J h/2π എന്നു സിദ്ധിക്കും. ഒരു അണുകേന്ദ്രത്തില്, പൌളിയുടെ സിദ്ധാന്തപ്രകാരം (2J + 1) ന്യൂക്ളിയോണുകള്ക്കു സംപൂര്ണ കോണീയ സംവേഗം (Total angular momentum) ഉണ്ടാകാവുന്നതാണ്. | ||
ഈ സങ്കല്പനങ്ങളെ അടിസ്ഥാനമാക്കി തുടരെയുള്ള അണുകേന്ദ്രോര്ജസ്തരങ്ങളില് ന്യൂക്ളിയോണുകളെ നിറച്ച് അണുകേന്ദ്രങ്ങള് ഓരോന്നായി ചെറുതുമുതല് വലുതുവരെ നിര്മിച്ചെടുക്കാന് കഴിയുമെന്നു മാത്രമല്ല, സംവൃതകവചങ്ങളെ സൂചിപ്പിക്കുന്ന എല്ലാ മാന്ത്രികസംഖ്യകളും കണ്ടെത്താന് കഴിയുകയും ചെയ്യും. ഇലക്ട്രോണികകവചങ്ങള്കൊണ്ട് അണുവിന്റെ ഘടനയെ ആവിഷ്കരിച്ച് മൂലകങ്ങളുടെ ആവര്ത്തകവര്ഗീകരണത്തെ (Periodic classification of elements) ബന്ധപ്പെടുത്തിയതുപോലെ, ന്യൂക്ളിയോണുകള് അടങ്ങിയ സംവൃതകവചങ്ങളാല് അണുകേന്ദ്രങ്ങള് നിര്മിതമായിരിക്കുന്നു എന്നു സങ്കല്പിക്കാന് കഴിയും. | ഈ സങ്കല്പനങ്ങളെ അടിസ്ഥാനമാക്കി തുടരെയുള്ള അണുകേന്ദ്രോര്ജസ്തരങ്ങളില് ന്യൂക്ളിയോണുകളെ നിറച്ച് അണുകേന്ദ്രങ്ങള് ഓരോന്നായി ചെറുതുമുതല് വലുതുവരെ നിര്മിച്ചെടുക്കാന് കഴിയുമെന്നു മാത്രമല്ല, സംവൃതകവചങ്ങളെ സൂചിപ്പിക്കുന്ന എല്ലാ മാന്ത്രികസംഖ്യകളും കണ്ടെത്താന് കഴിയുകയും ചെയ്യും. ഇലക്ട്രോണികകവചങ്ങള്കൊണ്ട് അണുവിന്റെ ഘടനയെ ആവിഷ്കരിച്ച് മൂലകങ്ങളുടെ ആവര്ത്തകവര്ഗീകരണത്തെ (Periodic classification of elements) ബന്ധപ്പെടുത്തിയതുപോലെ, ന്യൂക്ളിയോണുകള് അടങ്ങിയ സംവൃതകവചങ്ങളാല് അണുകേന്ദ്രങ്ങള് നിര്മിതമായിരിക്കുന്നു എന്നു സങ്കല്പിക്കാന് കഴിയും. | ||
| വരി 123: | വരി 127: | ||
<sup>1</sup>H<sub>1</sub>+Q | <sup>1</sup>H<sub>1</sub>+Q | ||
| - | എന്ന സമീകരണംകൊണ്ട് ഈ പ്രതിപ്രവര്ത്തനം വിശദമാക്കാം. ഇതില് | + | എന്ന സമീകരണംകൊണ്ട് ഈ പ്രതിപ്രവര്ത്തനം വിശദമാക്കാം. ഇതില് <sup>18</sup>H<sub>9</sub> അസ്ഥിരമായ യൌഗികാണുകേന്ദ്രമാണ്. Q അണുകേന്ദ്ര-പ്രതിപ്രവര്ത്തനോര്ജം (Nuclear reaction energy) ആണ്. ഇങ്ങനെയുള്ള പ്രതിപ്രവര്ത്തനത്തില് ഉള്പ്പെടുന്ന അണുകേന്ദ്രങ്ങളുടെയും കണങ്ങളുടെയും ദ്രവ്യമാനവും ഗതികോര്ജവും കണക്കിലെടുത്താല് M<sub>0</sub>+M<sub>1</sub>=M<sub>2</sub>+M<sub>3</sub>+ |
| - | (E<sub>1</sub>+E<sub>2</sub>-E<sub>3</sub>)=M<sub>2</sub>+M<sub>3</sub>+Q എന്ന സമീകരണം സിദ്ധിക്കും. ഇവിടെ M<sub>0</sub>, M<sub>1</sub>, M<sub>2</sub>, M<sub>3</sub> എന്നിവ യഥാക്രമം ആഘാതം ചെയ്യപ്പെട്ട അണുകേന്ദ്രത്തിന്റെയും ആഘാതം ഏല്പിച്ച കണത്തിന്റെയും ഉത്പന്ന-അണുകേന്ദ്രത്തിന്റെയും വമിക്കപ്പെട്ട കണത്തിന്റെയും ദ്രവ്യമാനമാണ്; E<sub>1</sub>, E<sub>2</sub>, E<sub>3</sub> എന്നിവ യഥാക്രമം M<sub>1</sub>, M<sub>2</sub>, M<sub>3</sub> എന്നിവയുടെ ഗതികോര്ജവും. ആഘാതമേറ്റ അണുകേന്ദ്രത്തിന്റെ ഗതികോര്ജം അവഗണിക്കാവുന്നതാണ്. Q ധനാത്മകമാണെങ്കില് പ്രതിപ്രവര്ത്തനം താപോന്മോചകവും (exothermic), ഋണാത്മകമാണെങ്കില് താപശോഷിതവും (endothermic), ആണ്. α-കണങ്ങളുടെ ആഘാതത്താല് ബോറോണ് (Boron) മുതല് കാല്ഷ്യം (Calcium) വരെയുള്ള മൂലകങ്ങള്ക്ക് (കാര്ബണും ഓക്സിജനും ഒഴികെ) മൂലകാന്തരണം (transmutation) സംഭവിക്കുന്നതാണ്. പുറത്തുപോകുന്ന കണം പ്രോട്ടോണ് ആയിരിക്കും. ഈ പ്രതിപ്രവര്ത്തനത്തെ -p എന്നു പറയുന്നു. | + | (E<sub>1</sub>+E<sub>2</sub>-E<sub>3</sub>)=M<sub>2</sub>+M<sub>3</sub>+Q എന്ന സമീകരണം സിദ്ധിക്കും. ഇവിടെ M<sub>0</sub>, M<sub>1</sub>, M<sub>2</sub>, M<sub>3</sub> എന്നിവ യഥാക്രമം ആഘാതം ചെയ്യപ്പെട്ട അണുകേന്ദ്രത്തിന്റെയും ആഘാതം ഏല്പിച്ച കണത്തിന്റെയും ഉത്പന്ന-അണുകേന്ദ്രത്തിന്റെയും വമിക്കപ്പെട്ട കണത്തിന്റെയും ദ്രവ്യമാനമാണ്; E<sub>1</sub>, E<sub>2</sub>, E<sub>3</sub> എന്നിവ യഥാക്രമം M<sub>1</sub>, M<sub>2</sub>, M<sub>3</sub> എന്നിവയുടെ ഗതികോര്ജവും. ആഘാതമേറ്റ അണുകേന്ദ്രത്തിന്റെ ഗതികോര്ജം അവഗണിക്കാവുന്നതാണ്. Q ധനാത്മകമാണെങ്കില് പ്രതിപ്രവര്ത്തനം താപോന്മോചകവും (exothermic), ഋണാത്മകമാണെങ്കില് താപശോഷിതവും (endothermic), ആണ്. α-കണങ്ങളുടെ ആഘാതത്താല് ബോറോണ് (Boron) മുതല് കാല്ഷ്യം (Calcium) വരെയുള്ള മൂലകങ്ങള്ക്ക് (കാര്ബണും ഓക്സിജനും ഒഴികെ) മൂലകാന്തരണം (transmutation) സംഭവിക്കുന്നതാണ്. പുറത്തുപോകുന്ന കണം പ്രോട്ടോണ് ആയിരിക്കും. ഈ പ്രതിപ്രവര്ത്തനത്തെ α-p എന്നു പറയുന്നു. |
<sup>10</sup>B<sub>5</sub> +<sup>4</sup>He<sub>2</sub>→ (<sup>14</sup>N<sub>7</sub>)→<sup>13</sup>C<sub>6</sub>+ | <sup>10</sup>B<sub>5</sub> +<sup>4</sup>He<sub>2</sub>→ (<sup>14</sup>N<sub>7</sub>)→<sup>13</sup>C<sub>6</sub>+ | ||
| - | Q;Q=+ | + | Q;Q=+4.4 MeV |
10<sup>5</sup> മുതല് 10<sup>7</sup> വരെ α-കണങ്ങളുടെ ആഘാതമേല്ക്കുമ്പോഴാണ് ഒരു പ്രോട്ടോണ്കണം ഉണ്ടാകാന് സാധ്യതയുള്ളത്. | 10<sup>5</sup> മുതല് 10<sup>7</sup> വരെ α-കണങ്ങളുടെ ആഘാതമേല്ക്കുമ്പോഴാണ് ഒരു പ്രോട്ടോണ്കണം ഉണ്ടാകാന് സാധ്യതയുള്ളത്. | ||
| - | '''ആല്ഫാ-ന്യൂട്ടോണ് പ്രതിപ്രവര്ത്തനം.''' ഒരു അണുകേന്ദ്രം | + | '''ആല്ഫാ-ന്യൂട്ടോണ് പ്രതിപ്രവര്ത്തനം.''' ഒരു അണുകേന്ദ്രം αകണത്തെ പിടിച്ചെടുക്കുമ്പോഴെല്ലാം പ്രോട്ടോണ്കണം ഉണ്ടാകണമെന്നില്ല; ഒരു ന്യൂട്രോണ്കണം ആകാനും സാധ്യതയുണ്ട്. ന്യൂട്രോണ്കണത്തെ ചാഡ്വിക് (chadwick) കണ്ടുപിടിച്ചതുതന്നെ, α-കണങ്ങള്കൊണ്ട് ബെരീലിയത്തെ (Beryllium) ആഘാതം ചെയ്തപ്പോഴാണ്. |
<sup>9</sup>Be<sub>4</sub> + <sup>4</sup>He<sub>2</sub> &rarr(<sup>13</sup>C<sub>6</sub>)→<sup>12</sup>C<sub>6</sub> | <sup>9</sup>Be<sub>4</sub> + <sup>4</sup>He<sub>2</sub> &rarr(<sup>13</sup>C<sub>6</sub>)→<sup>12</sup>C<sub>6</sub> | ||
| വരി 137: | വരി 141: | ||
| - | '''പ്രോട്ടോണിന്റെ ആഘാതത്താല് സംഭവിക്കാവുന്ന മൂലകാന്തരണം''' (Transmutation by protons). ലിഥിയത്തെ പ്രോട്ടോണ്കണംകൊണ്ട് ആഘാതം ഏല്പിച്ചപ്പോള് ഹീലിയം കണങ്ങളുണ്ടായി. | + | '''പ്രോട്ടോണിന്റെ ആഘാതത്താല് സംഭവിക്കാവുന്ന മൂലകാന്തരണം''' (Transmutation by protons). ലിഥിയത്തെ പ്രോട്ടോണ്കണംകൊണ്ട് ആഘാതം ഏല്പിച്ചപ്പോള് ഹീലിയം കണങ്ങളുണ്ടായി. കോക്ക്രോഫ്ട്ടും വില്സണും ആണ് ഈ പരീക്ഷണം നടത്തിയത്. 0.1 മുതല് 0.7 Mev വരെ ഊര്ജമുള്ള പ്രോട്ടോണ്കണം അവര് ഉപയോഗിച്ചു. |
<sup>11</sup>B<sub>5</sub> + <sup>1</sup>H<sub>1</sub>→ (<sup>12</sup>C<sub>6</sub>)→<sup>8</sup>Be<sub>4</sub> | <sup>11</sup>B<sub>5</sub> + <sup>1</sup>H<sub>1</sub>→ (<sup>12</sup>C<sub>6</sub>)→<sup>8</sup>Be<sub>4</sub> | ||
| വരി 150: | വരി 154: | ||
| - | '''പ്രോട്രോണ്-ഗാമ പ്രതിപ്രവര്ത്തനം.''' ചില സന്ദര്ഭങ്ങളില് ആഘാതം ഏല്പിക്കുന്ന പ്രോട്ടോണിനെ ആഘാതം ഏല്ക്കുന്ന അണുകേന്ദ്രം പിടിച്ചെടുത്തുവെന്നു വരാം. അപ്പോള് ഉണ്ടാകുന്ന യൌഗിക-അണുകേന്ദ്രം അസ്ഥിരമാകയാല് | + | '''പ്രോട്രോണ്-ഗാമ പ്രതിപ്രവര്ത്തനം.''' ചില സന്ദര്ഭങ്ങളില് ആഘാതം ഏല്പിക്കുന്ന പ്രോട്ടോണിനെ ആഘാതം ഏല്ക്കുന്ന അണുകേന്ദ്രം പിടിച്ചെടുത്തുവെന്നു വരാം. അപ്പോള് ഉണ്ടാകുന്ന യൌഗിക-അണുകേന്ദ്രം അസ്ഥിരമാകയാല് γ-രശ്മി വികിരണം ചെയ്ത് സുസ്ഥിരത ലഭിക്കുന്നു. |
| - | <sup>7</sup>Li<sub>3</sub> + <sup>1</sup>H<sub>1</sub>→ (<sup>8</sup>Be<sub>4</sub>)→<sup>8</sup>Be<sub>4</sub> + | + | <sup>7</sup>Li<sub>3</sub> + <sup>1</sup>H<sub>1</sub>→ (<sup>8</sup>Be<sub>4</sub>)→<sup>8</sup>Be<sub>4</sub> + γ |
| വരി 193: | വരി 197: | ||
Nuclear fission | Nuclear fission | ||
| - | 92-ല് കവിഞ്ഞ അണുസംഖ്യയുള്ള മൂലകങ്ങള് കൃത്രിമമായി സൃഷ്ടിക്കാന് പരിശ്രമിച്ചപ്പോള് കണ്ടുപിടിക്കപ്പെട്ട ഒരു പ്രതിഭാസമാണ് അണുകേന്ദ്ര വിഘടനം. ഈ പരീക്ഷണങ്ങളില് ന്യൂട്രോണ്-γ പ്രതിപ്രവര്ത്തനങ്ങളും അവയെത്തുടര്ന്നുള്ള ഉത്പന്ന-അണുകേന്ദ്ര(product nucleus)ത്തിന്റെβ-ക്ഷയ ( β-decay)വും ആണ് സംഭവിച്ചത്. നേരത്തെ നടത്തിയ പരീക്ഷണങ്ങളില് യുറേനിയത്തെ ന്യൂട്രോണുകള്കൊണ്ട് ആഘാതം ചെയ്യപ്പെടുകയാണുണ്ടായത്. ഈ പരീക്ഷണങ്ങളില് പാരയുറേനിയം (Trans-Urenium) ലഭിച്ചതുകൂടാതെ റേഡിയത്തിന്റെ β-റേഡിയോ ആക്റ്റീവ് ഐസോടോപ്പുകളും β-radio active isotopes) കൂടി കാണപ്പെട്ടു. മേല്പറഞ്ഞ ന്യൂക്ളിയൈഡിനു ക്ഷയം സംഭവിച്ചപ്പോള് ലഭിച്ച വ്യുത്പന്നങ്ങള് ആക്റ്റിനിയ(Actinum)ത്തിന്റെ ഐസോടോപ്പുകളാണോ എന്നും സംശയിച്ചു. എന്നാല് ഈ അനുമാനങ്ങള് മറ്റു ചില വസ്തുതകള് പരിഗണിച്ചപ്പോള് ശരിയല്ലെന്നറിഞ്ഞു. റേഡിയത്തിന്റെ ഐസോടോപ്പുകളാണെന്നു സംശയിച്ചത് വാസ്തവത്തില് ബേരിയത്തിന്റേതാണെന്നും ആക്റ്റിനിയത്തിന്റെ ഐസോടോപ്പുകളാണെന്ന് അനുമാനിച്ചതു യഥാര്ഥത്തില് ലന്ഥാനത്തിന്റേതാണെന്നും ഹാന് (Hahn), സ്റ്റ്രാസ്മാന് ( | + | 92-ല് കവിഞ്ഞ അണുസംഖ്യയുള്ള മൂലകങ്ങള് കൃത്രിമമായി സൃഷ്ടിക്കാന് പരിശ്രമിച്ചപ്പോള് കണ്ടുപിടിക്കപ്പെട്ട ഒരു പ്രതിഭാസമാണ് അണുകേന്ദ്ര വിഘടനം. ഈ പരീക്ഷണങ്ങളില് ന്യൂട്രോണ്-γ പ്രതിപ്രവര്ത്തനങ്ങളും അവയെത്തുടര്ന്നുള്ള ഉത്പന്ന-അണുകേന്ദ്ര(product nucleus)ത്തിന്റെβ-ക്ഷയ ( β-decay)വും ആണ് സംഭവിച്ചത്. നേരത്തെ നടത്തിയ പരീക്ഷണങ്ങളില് യുറേനിയത്തെ ന്യൂട്രോണുകള്കൊണ്ട് ആഘാതം ചെയ്യപ്പെടുകയാണുണ്ടായത്. ഈ പരീക്ഷണങ്ങളില് പാരയുറേനിയം (Trans-Urenium) ലഭിച്ചതുകൂടാതെ റേഡിയത്തിന്റെ β-റേഡിയോ ആക്റ്റീവ് ഐസോടോപ്പുകളും β-radio active isotopes) കൂടി കാണപ്പെട്ടു. മേല്പറഞ്ഞ ന്യൂക്ളിയൈഡിനു ക്ഷയം സംഭവിച്ചപ്പോള് ലഭിച്ച വ്യുത്പന്നങ്ങള് ആക്റ്റിനിയ(Actinum)ത്തിന്റെ ഐസോടോപ്പുകളാണോ എന്നും സംശയിച്ചു. എന്നാല് ഈ അനുമാനങ്ങള് മറ്റു ചില വസ്തുതകള് പരിഗണിച്ചപ്പോള് ശരിയല്ലെന്നറിഞ്ഞു. റേഡിയത്തിന്റെ ഐസോടോപ്പുകളാണെന്നു സംശയിച്ചത് വാസ്തവത്തില് ബേരിയത്തിന്റേതാണെന്നും ആക്റ്റിനിയത്തിന്റെ ഐസോടോപ്പുകളാണെന്ന് അനുമാനിച്ചതു യഥാര്ഥത്തില് ലന്ഥാനത്തിന്റേതാണെന്നും ഹാന് (Hahn), സ്റ്റ്രാസ്മാന് (Straussmann) എന്നീ ശാസ്ത്രജ്ഞന്മാര് പരീക്ഷണങ്ങള്വഴി തെളിയിച്ചു. യുറേനിയത്തില്നിന്നു <sup>140</sup>La<sub>57</sub>, <sup>139</sup>Ba<sub>56</sub> എന്നീ ന്യൂക്ളിയൈഡുകള് ലഭിച്ചതുകൊണ്ട് ഏതോ അജ്ഞാതമായ അണുകേന്ദ്രപ്രതിപ്രവര്ത്തനം ആണ് അവിടെ നടന്നതെന്നും യുറേനിയം അണുകേന്ദ്രം രണ്ടായി പിളര്ന്നിരിക്കാമെന്നും അനുമാനിച്ചു. തുടര്ന്നുണ്ടായ പരീക്ഷണങ്ങള് സ്റ്റ്രോണ്ഷിയം (Strontium) (S = 31), യിട്രിയം (Yttrium) (Z = 39), ക്രിപ്ടോണ് (Krypton) (Z = 36), ക്സിനോണ് (Xenon) (Z = 54) എന്നീ മൂലകങ്ങളും ഐസോടോപ്പുകളും ഉത്പന്നങ്ങളില് കണ്ടെത്തി. കൂടാതെ ബ്രോമിന് (Bromine), മോളിബ്ഡനം (Molybdenum), റൂബീഡിയം (Rubedium), ആന്റിമണി (Antimony), അയഡിന് (Iodine) എന്നിവയുടെ അണുകേന്ദ്രങ്ങളും ഉള്ളതായി അറിഞ്ഞു. യുറേനിയം അണുകേന്ദ്രം രണ്ടായി വിഭജിക്കപ്പെട്ടിരിക്കണമെന്നു മനസ്സിലാക്കാം. ഈ പ്രതിഭാസത്തെയാണ് അണുകേന്ദ്രവിഘടനമെന്നു പറയുന്നത്. യുറേനിയം-235 (<sup>235</sup>U)-അണുകേന്ദ്രത്തെ വിഘടനം ചെയ്യാന് താപീയ ന്യൂട്രോണ് (Thermal neutron) മതിയാകും. (<sup>238</sup>U)-നെ വിഘടനം ചെയ്യാന് കൂടുതല് ഊര്ജമുള്ള ന്യൂട്രോണുകള് വേണം. യുറേനിയം അണുകേന്ദ്രം മാത്രമല്ല, അണുസംഖ്യ 200-ല് കൂടുതലുള്ള പല അണുകേന്ദ്രങ്ങളും വിഘടനത്തിനു വിധേയമാണ്. വിഘടനം നടക്കുന്നതിനു ന്യൂട്രോണ് കണങ്ങള് തന്നെ വേണമെന്നില്ല. ഫോട്ടോണുകള്, ഇലക്ട്രോണുകള്, മെസോണുകള്, പ്രോട്ടോണുകള്, ഡ്യൂട്ടറോണുകള്, α-കണങ്ങള് എന്നിവയുടെ പ്രചോദനത്താല് വിഘടനം സംഭവിക്കാം. |
<sup>235</sup>U<sub>92</sub> + <sup>1</sup>n<sub>0</sub> →(<sup>236</sup>U<sub>92</sub>)→ X + Y | <sup>235</sup>U<sub>92</sub> + <sup>1</sup>n<sub>0</sub> →(<sup>236</sup>U<sub>92</sub>)→ X + Y | ||
| വരി 199: | വരി 203: | ||
[[Image:pno.344Vigha.png|right|]] | [[Image:pno.344Vigha.png|right|]] | ||
| - | ഇതു യുറേനിയം-235 അണുകേന്ദ്രത്തിന്റെ വിഘടനത്തെ കുറിക്കുന്നു. ഇതില് n എന്നതു താപീയ ന്യൂട്രോണും, x,y എന്നിവ പ്രാഥമിക വിഘടനോത്പന്നങ്ങളും (primary fission products) ആണ്. ചിത്രത്തില് വിഘടനോത്പന്നങ്ങളുടെ സാംഖ്യിക പ്രകൃതം (statistical nature) സൂചിപ്പിക്കുന്നു. അണുസംഖ്യയെ ആധാരമാക്കി വിഘടനോത്പന്നങ്ങളുടെ വിതരണം ഈ ചിത്രത്തില്നിന്നു മനസ്സിലാക്കാം. അണുസംഖ്യ 118 ആയാല് സമമിത വിഘടനം (Symmetric fission) വളരെ അപൂര്വമാണെന്നും (0.01ശ.മാ.) ഇത് ഏറ്റവും സംഭാവ്യമാകുന്നത് 96,140 എന്നീ അണുസംഖ്യയുള്ള ഖണ്ഡങ്ങള് ഉണ്ടാകുന്ന വിഘടനമാണെന്നും ചിത്രം സൂചിപ്പിക്കുന്നു. മധ്യത്തിലുള്ള അല്പതമത്തെ അടിസ്ഥാനമാക്കി ലേഖ (curve) സമമിതം ( | + | ഇതു യുറേനിയം-235 അണുകേന്ദ്രത്തിന്റെ വിഘടനത്തെ കുറിക്കുന്നു. ഇതില് n എന്നതു താപീയ ന്യൂട്രോണും, x,y എന്നിവ പ്രാഥമിക വിഘടനോത്പന്നങ്ങളും (primary fission products) ആണ്. ചിത്രത്തില് വിഘടനോത്പന്നങ്ങളുടെ സാംഖ്യിക പ്രകൃതം (statistical nature) സൂചിപ്പിക്കുന്നു. അണുസംഖ്യയെ ആധാരമാക്കി വിഘടനോത്പന്നങ്ങളുടെ വിതരണം ഈ ചിത്രത്തില്നിന്നു മനസ്സിലാക്കാം. അണുസംഖ്യ 118 ആയാല് സമമിത വിഘടനം (Symmetric fission) വളരെ അപൂര്വമാണെന്നും (0.01ശ.മാ.) ഇത് ഏറ്റവും സംഭാവ്യമാകുന്നത് 96,140 എന്നീ അണുസംഖ്യയുള്ള ഖണ്ഡങ്ങള് ഉണ്ടാകുന്ന വിഘടനമാണെന്നും ചിത്രം സൂചിപ്പിക്കുന്നു. മധ്യത്തിലുള്ള അല്പതമത്തെ അടിസ്ഥാനമാക്കി ലേഖ (curve) സമമിതം (symmetrical) ആണെന്നും കാണാം. ഓരോ ഘനഖണ്ഡത്തിനും അനുരൂപമായ ലഘുഖണ്ഡവും ഉണ്ടായിരിക്കണം. രണ്ടു ഖണ്ഡങ്ങളും അസ്ഥിരമാണ്. പ്രാഥമിക ഖണ്ഡങ്ങള് ശൃംഖലാക്രമത്തില് (chain like) ക്ഷയിച്ച് ഒടുവില് സ്ഥിരമൂലകങ്ങളായി അവശേഷിക്കുന്നു. വിഘടനം കഴിഞ്ഞ ഉടനെ പ്രാഥമിക ഖണ്ഡങ്ങളില്നിന്നു ശ.ശ. 2.5 ന്യൂട്രോണുകള് വമിക്കപ്പെടുന്നതാണ്. അവയില് 99 ശ.മാ.വും 10<sup>-13</sup> സെക്കന്ഡിനകം പ്രത്യക്ഷപ്പെടുന്നതിനാല് അവയെ ക്ഷണിക ന്യൂട്രോണ് (prompt neutron) എന്നു വിളിക്കുന്നു. ഏതാനും ന്യൂട്രോണുകള് അല്പം താമസിച്ചു പ്രത്യക്ഷപ്പെടുന്നു. |
=== വിഘടനത്തില്നിന്നു മോചിപ്പിക്കപ്പെടുന്ന ഊര്ജം === | === വിഘടനത്തില്നിന്നു മോചിപ്പിക്കപ്പെടുന്ന ഊര്ജം === | ||
| - | വിഘടനപ്രക്രിയയില് വളരെ അധികം ഊര്ജം ഉടന്തന്നെ മോചിപ്പിക്കപ്പെടുന്നു. അല്പം ശേഷിക്കുന്നതുതന്നെ പ്രാഥമിക ഖണ്ഡങ്ങള് ക്ഷയിക്കുമ്പോള് മോചിപ്പിക്കപ്പെടുന്നു. ആകാശത്തിലാണ് വിഘടനം സംഭവിക്കുന്നതെങ്കില് ആകെ മോചിപ്പിക്കപ്പെടുന്ന ഊര്ജം വിഘടനഖണ്ഡങ്ങളുടെ ഗതികോര്ജമായി പ്രത്യക്ഷപ്പെടുന്നു. ഒരു വലിയ അവശോഷക(absorber)ത്തിലാണ് വിഘടനം സംഭവിക്കുന്നതെങ്കില് ആകെ മോചിപ്പിക്കപ്പെടുന്ന ഊര്ജം അവശോഷകത്തില് താപമായിത്തീരുന്നു. താപീയ ന്യൂട്രോണുകള്കൊണ്ടു നടക്കുന്ന വിഘടനത്തില് 120 മുതല് 180 വരെ | + | വിഘടനപ്രക്രിയയില് വളരെ അധികം ഊര്ജം ഉടന്തന്നെ മോചിപ്പിക്കപ്പെടുന്നു. അല്പം ശേഷിക്കുന്നതുതന്നെ പ്രാഥമിക ഖണ്ഡങ്ങള് ക്ഷയിക്കുമ്പോള് മോചിപ്പിക്കപ്പെടുന്നു. ആകാശത്തിലാണ് വിഘടനം സംഭവിക്കുന്നതെങ്കില് ആകെ മോചിപ്പിക്കപ്പെടുന്ന ഊര്ജം വിഘടനഖണ്ഡങ്ങളുടെ ഗതികോര്ജമായി പ്രത്യക്ഷപ്പെടുന്നു. ഒരു വലിയ അവശോഷക(absorber)ത്തിലാണ് വിഘടനം സംഭവിക്കുന്നതെങ്കില് ആകെ മോചിപ്പിക്കപ്പെടുന്ന ഊര്ജം അവശോഷകത്തില് താപമായിത്തീരുന്നു. താപീയ ന്യൂട്രോണുകള്കൊണ്ടു നടക്കുന്ന വിഘടനത്തില് 120 മുതല് 180 വരെ MeVഊര്ജം മോചിപ്പിക്കപ്പെടുന്നുണ്ട്. ഇതു ഘനഅണുകേന്ദ്രത്തിനുള്ള ദ്രവ്യമാനത്തിന്റെ 0.1 ശ.മാ. ഊര്ജത്തിനു തുല്യമാണ്. |
| - | വിഘടനത്തിന്റെ ശ്രദ്ധാര്ഹമായ ഗുണങ്ങള് മനസ്സിലാക്കാന് കഴിഞ്ഞപ്പോള് അതിനെക്കുറിച്ചുള്ള ശാസ്ത്രീയ പഠനത്തില് താത്പര്യം വളരെ വര്ധിച്ചു. അണുകേന്ദ്രത്തിന്റെ ബിന്ദുമാതൃകയെ ആസ്പദമാക്കി ബോര്, വീലര് (Bohr,Wheeler) എന്നീ ശാസ്ത്രജ്ഞന്മാര്, വിഘടനത്തിന്റെ പല ഗുണങ്ങള്ക്കും തക്കതായ വിശദീകരണം നല്കി. പല അണുകേന്ദ്രങ്ങള്ക്കും സമമിത വിഘടനത്തിനു വേണ്ടിവരുന്ന ഉത്തേജനോര്ജ(activation energy) ത്തിന്റെ അളവ് അവര് നിര്ണയിച്ചു. ഘനഅണുകേന്ദ്രത്തിനു മന്ദഗതിയുള്ള ന്യൂട്രോണ് കൊണ്ടു വിഘടനം സംഭവിക്കാനുള്ള സാധ്യതയെപ്പറ്റിയും അവര് പഠനം നടത്തി. മൌലിക ദ്രവ്യമാനസൂത്രമുപയോഗിച്ചാണ് ഇവയെല്ലാം മനസ്സിലാക്കിയത്. താപീയ ന്യൂട്രോണുകള്ക്ക് <sup>235</sup>U-നെ വിഘടനം ചെയ്യാന് കഴിയുമെന്നും | + | വിഘടനത്തിന്റെ ശ്രദ്ധാര്ഹമായ ഗുണങ്ങള് മനസ്സിലാക്കാന് കഴിഞ്ഞപ്പോള് അതിനെക്കുറിച്ചുള്ള ശാസ്ത്രീയ പഠനത്തില് താത്പര്യം വളരെ വര്ധിച്ചു. അണുകേന്ദ്രത്തിന്റെ ബിന്ദുമാതൃകയെ ആസ്പദമാക്കി ബോര്, വീലര് (Bohr,Wheeler) എന്നീ ശാസ്ത്രജ്ഞന്മാര്, വിഘടനത്തിന്റെ പല ഗുണങ്ങള്ക്കും തക്കതായ വിശദീകരണം നല്കി. പല അണുകേന്ദ്രങ്ങള്ക്കും സമമിത വിഘടനത്തിനു വേണ്ടിവരുന്ന ഉത്തേജനോര്ജ(activation energy) ത്തിന്റെ അളവ് അവര് നിര്ണയിച്ചു. ഘനഅണുകേന്ദ്രത്തിനു മന്ദഗതിയുള്ള ന്യൂട്രോണ് കൊണ്ടു വിഘടനം സംഭവിക്കാനുള്ള സാധ്യതയെപ്പറ്റിയും അവര് പഠനം നടത്തി. മൌലിക ദ്രവ്യമാനസൂത്രമുപയോഗിച്ചാണ് ഇവയെല്ലാം മനസ്സിലാക്കിയത്. താപീയ ന്യൂട്രോണുകള്ക്ക് <sup>235</sup>U-നെ വിഘടനം ചെയ്യാന് കഴിയുമെന്നും <sup>238</sup>U-നെ വിഘടനം ചെയ്യാന് അവയ്ക്കു സാധിക്കുന്നതല്ലെന്നും അവര് സ്പഷ്ടമാക്കി. |
| വരി 215: | വരി 219: | ||
സാധാരണ യുറേനിയം ലോഹത്തില് <sup>235</sup>U 140-ല് ഒരംശം മാത്രമാണുള്ളത്. ബാക്കിയുള്ളതില് ഭൂരിഭാഗവും <sup>238</sup>U ആണ്. ഒരു ശൃംഖലാപ്രതിപ്രവര്ത്തനത്തില് വരണമെങ്കില് അടുത്ത തലമുറയില് ജനിക്കുന്ന ന്യൂട്രോണുകളുടെ എണ്ണം ഈ തലമുറയില് ഉള്ളതിനേക്കാള് കൂടുതലായിരിക്കണം. അതായത്, 100 ന്യൂട്രോണുകള് പ്രാരംഭവിഘടനത്തെ പ്രോത്സാഹിപ്പിക്കുന്നുവെങ്കില് അടുത്ത തലമുറയില് വിഘടനത്തിലേര്പ്പെടാന് കഴിവുള്ള 100-ല് കൂടുതല് ന്യൂട്രോണുകള് ഉണ്ടാകണം. അങ്ങനെയുണ്ടാകണമെങ്കില് വിഘടനപ്രക്രിയ അനുസ്യൂതമായി തുടരേണ്ടതാണ്. | സാധാരണ യുറേനിയം ലോഹത്തില് <sup>235</sup>U 140-ല് ഒരംശം മാത്രമാണുള്ളത്. ബാക്കിയുള്ളതില് ഭൂരിഭാഗവും <sup>238</sup>U ആണ്. ഒരു ശൃംഖലാപ്രതിപ്രവര്ത്തനത്തില് വരണമെങ്കില് അടുത്ത തലമുറയില് ജനിക്കുന്ന ന്യൂട്രോണുകളുടെ എണ്ണം ഈ തലമുറയില് ഉള്ളതിനേക്കാള് കൂടുതലായിരിക്കണം. അതായത്, 100 ന്യൂട്രോണുകള് പ്രാരംഭവിഘടനത്തെ പ്രോത്സാഹിപ്പിക്കുന്നുവെങ്കില് അടുത്ത തലമുറയില് വിഘടനത്തിലേര്പ്പെടാന് കഴിവുള്ള 100-ല് കൂടുതല് ന്യൂട്രോണുകള് ഉണ്ടാകണം. അങ്ങനെയുണ്ടാകണമെങ്കില് വിഘടനപ്രക്രിയ അനുസ്യൂതമായി തുടരേണ്ടതാണ്. | ||
| - | സാധാരണ യുറേനിയം ഒരു മന്ദീകാരി(moderator)യില് ചിതറിവച്ചിരിക്കുന്നുവെന്നു വിചാരിക്കുക. പുനരുത്പാദനഗുണകം k= ηepf എന്നെഴുതാം. ഇതില് യുറേനിയം <sup>235</sup>U അണുകേന്ദ്രം ഒരു താപീയ ന്യൂട്രോണിനെ അവശോഷണം ചെയ്യുമ്പോള് ഉത്പാദിപ്പിക്കപ്പെടുന്ന ന്യൂട്രോണുകളുടെ ശ.ശ. എണ്ണം ആണ് η. ശീഘ്രഗതിയുള്ള ഈ ന്യൂട്രോണുകള്ക്ക് ഉന്നത-ഊര്ജമുള്ളതുകൊണ്ട് <sup>238</sup>U അണുകേന്ദ്രങ്ങളെ വിഘടനം ചെയ്യാനുള്ള കഴിവുണ്ടാകുന്നു; c ശീഘ്രവിഘടനഗുണകം (e > 1) ആണ്. മന്ദീകാരി (സാധാരണ ഉപയോഗിക്കുന്നതു ഗ്രാഫൈറ്റ് ആണ്) ന്യൂട്രോണുകളെ മന്ദഗതിയിലാക്കുമ്പോള് <sup>238</sup>U അവയില് ചിലതിനെ അനുനാദാവശോഷണം (resonance absorption) കൊണ്ട് അകറ്റിക്കളയുന്നു. ഒടുവില് ലഭിക്കുന്ന താപീയന്യൂട്രോണുകളില് ഏതാനും എണ്ണത്തെ മന്ദീകാരിതന്നെ അവശോഷണം ചെയ്യുന്നു. ശേഷിക്കുന്ന അംശം f ആണ്. ഇതിനെ താപീയ-ഉപയോഗ ഗുണകം (thermal utilisation factor) എന്നു പറയുന്നു. റിയാക്റ്ററിന്റെ വലുപ്പം അപരിമിതമല്ലാത്തതിനാല് അതിന്റെ പ്രതലത്തില്നിന്നു ന്യൂട്രോണുകള് ചോര്ന്നുപോകാനിടയുണ്ട്. ഈ കാരണത്താല് പ്രതിപ്രവര്ത്തനം നടക്കണമെങ്കില് റിയാക്റ്ററിന് ഒരു ക്രാന്തിക വലുപ്പമോ (critical size) അതില് കൂടുതലോ ഉണ്ടായിരിക്കണം. അണു-ഊര്ജം അനുസ്യൂതമായി മോചിപ്പിക്കപ്പെടണമെങ്കില് k( =ηepf)-യുടെ മൂല്യം 1-നേക്കാള് വലുതായിരിക്കണം. | + | സാധാരണ യുറേനിയം ഒരു മന്ദീകാരി(moderator)യില് ചിതറിവച്ചിരിക്കുന്നുവെന്നു വിചാരിക്കുക. പുനരുത്പാദനഗുണകം k= ηepf എന്നെഴുതാം. ഇതില് യുറേനിയം <sup>235</sup>U അണുകേന്ദ്രം ഒരു താപീയ ന്യൂട്രോണിനെ അവശോഷണം ചെയ്യുമ്പോള് ഉത്പാദിപ്പിക്കപ്പെടുന്ന ന്യൂട്രോണുകളുടെ ശ.ശ. എണ്ണം ആണ് η. ശീഘ്രഗതിയുള്ള ഈ ന്യൂട്രോണുകള്ക്ക് ഉന്നത-ഊര്ജമുള്ളതുകൊണ്ട് <sup>238</sup>U അണുകേന്ദ്രങ്ങളെ വിഘടനം ചെയ്യാനുള്ള കഴിവുണ്ടാകുന്നു; c ശീഘ്രവിഘടനഗുണകം (e > 1) ആണ്. മന്ദീകാരി (സാധാരണ ഉപയോഗിക്കുന്നതു ഗ്രാഫൈറ്റ് ആണ്) ന്യൂട്രോണുകളെ മന്ദഗതിയിലാക്കുമ്പോള് <sup>238</sup>U അവയില് ചിലതിനെ അനുനാദാവശോഷണം (resonance absorption) കൊണ്ട് അകറ്റിക്കളയുന്നു. ഒടുവില് ലഭിക്കുന്ന താപീയന്യൂട്രോണുകളില് ഏതാനും എണ്ണത്തെ മന്ദീകാരിതന്നെ അവശോഷണം ചെയ്യുന്നു. ശേഷിക്കുന്ന അംശം f ആണ്. ഇതിനെ താപീയ-ഉപയോഗ ഗുണകം (thermal utilisation factor) എന്നു പറയുന്നു. റിയാക്റ്ററിന്റെ വലുപ്പം അപരിമിതമല്ലാത്തതിനാല് അതിന്റെ പ്രതലത്തില്നിന്നു ന്യൂട്രോണുകള് ചോര്ന്നുപോകാനിടയുണ്ട്. ഈ കാരണത്താല് പ്രതിപ്രവര്ത്തനം നടക്കണമെങ്കില് റിയാക്റ്ററിന് ഒരു ക്രാന്തിക വലുപ്പമോ (critical size) അതില് കൂടുതലോ ഉണ്ടായിരിക്കണം. അണു-ഊര്ജം അനുസ്യൂതമായി മോചിപ്പിക്കപ്പെടണമെങ്കില് k( =ηepf)-യുടെ മൂല്യം 1-നേക്കാള് വലുതായിരിക്കണം. k-യുടെ മൂല്യം 1-നേക്കാള് വലുതായിരിക്കുന്നവിധം റിയാക്റ്റര് സംവിധാനം ചെയ്യുന്നു. കാഡ്മിയം നിയന്ത്രണദണ്ഡുകള് (Cadmium control rods) ഉപയോഗിച്ച് ന്യൂട്രോണുകളെ അവശോഷണം ചെയ്ത് k-യുടെ മൂല്യം 1-ല് കുറവാക്കി വിഘടനപ്രതിപ്രവര്ത്തനത്തെ നിയന്ത്രിക്കാവുന്നതാണ്. ഇതുപോലെ ഒരു റിയാക്റ്റര് ഫെര്മി എന്ന ശാസ്ത്രജ്ഞനും സഹപ്രവര്ത്തകരും ആദ്യമായി സംവിധാനം ചെയ്തു. ഷിക്കാഗോ സര്വകലാശാലയില് 1942 ഡി. 2-ന് ആണ് ഇതുണ്ടായത്. |
ശീഘ്രതയുള്ള വിഘടനപ്രതിപ്രവര്ത്തനം ആണ് അണുബോംബു സ്ഫോടനത്തില് സംഭവിക്കുന്നത്. അണുബോംബ് സ്ഫോടനം ചെയ്യുമ്പോള്, താത്ത്വികവശത്ത് k എന്ന ഗുണാങ്കം വളരെ വലുതാകുന്നു. ക്രാന്തികവലുപ്പത്തില് അല്പം കുറവുള്ളതും അകലെ സംവിധാനം ചെയ്തിട്ടുള്ളതുമായ രണ്ടു ശുദ്ധ യുറേനിയം-235 ലോഹക്കട്ടികള് പെട്ടെന്ന് അടുപ്പിച്ച് ആകെയുള്ള വലുപ്പം ക്രാന്തിക വലുപ്പത്തെക്കാള് കൂടുതലാക്കി വിഘടനപ്രതിപ്രവര്ത്തനം അതിവേഗത്തില് നടത്തി അണു-ഊര്ജം ഭീമമായ തോതില് മോചിപ്പിക്കുകയാണ് ചെയ്യുന്നത്. ഇതാണ് അണുബോംബ് പ്രവര്ത്തനത്തിലടങ്ങിയിരിക്കുന്ന തത്ത്വം. നോ: അണുബോംബ് | ശീഘ്രതയുള്ള വിഘടനപ്രതിപ്രവര്ത്തനം ആണ് അണുബോംബു സ്ഫോടനത്തില് സംഭവിക്കുന്നത്. അണുബോംബ് സ്ഫോടനം ചെയ്യുമ്പോള്, താത്ത്വികവശത്ത് k എന്ന ഗുണാങ്കം വളരെ വലുതാകുന്നു. ക്രാന്തികവലുപ്പത്തില് അല്പം കുറവുള്ളതും അകലെ സംവിധാനം ചെയ്തിട്ടുള്ളതുമായ രണ്ടു ശുദ്ധ യുറേനിയം-235 ലോഹക്കട്ടികള് പെട്ടെന്ന് അടുപ്പിച്ച് ആകെയുള്ള വലുപ്പം ക്രാന്തിക വലുപ്പത്തെക്കാള് കൂടുതലാക്കി വിഘടനപ്രതിപ്രവര്ത്തനം അതിവേഗത്തില് നടത്തി അണു-ഊര്ജം ഭീമമായ തോതില് മോചിപ്പിക്കുകയാണ് ചെയ്യുന്നത്. ഇതാണ് അണുബോംബ് പ്രവര്ത്തനത്തിലടങ്ങിയിരിക്കുന്ന തത്ത്വം. നോ: അണുബോംബ് | ||
| വരി 236: | വരി 240: | ||
<sup>2</sup>D<sub>1</sub> +<sup>2</sup>D<sub>1</sub>→ <sup>4</sup>He<sub>2</sub> | <sup>2</sup>D<sub>1</sub> +<sup>2</sup>D<sub>1</sub>→ <sup>4</sup>He<sub>2</sub> | ||
| - | ഇവിടെ ലഭിക്കുന്ന ഊര്ജം 24 MeV ആണ്. സോഡിയവും നിയോണും സംയോജിപ്പിച്ച് ഒരു | + | ഇവിടെ ലഭിക്കുന്ന ഊര്ജം 24 MeV ആണ്. സോഡിയവും നിയോണും സംയോജിപ്പിച്ച് ഒരു amu ലഭിക്കുന്ന ഊര്ജത്തിന്റെ 11 മടങ്ങാണ് ഒരു amu-ന് ഡ്യൂട്ടറോണ് സംയോജിപ്പിച്ചു ലഭിക്കുന്ന ഊര്ജം. ഒരു ഗ്രാം <sup>235</sup>U വിഘടനം ചെയ്തു ലഭിക്കുന്ന ഊര്ജം 22,000 കി.വാ.മ. ആയിരിക്കെ ഡ്യൂട്ടറോണുകള് സംയോജിപ്പിച്ച് ഹീലിയം അണുകേന്ദ്രമാക്കുമ്പോള് ലഭിക്കുന്ന ഊര്ജം 16,000 കി.വാ.മ. ആണ്. ഒരു ഗ്രാം ഹൈഡ്രജന് സംയോജിപ്പിച്ച് ഹീലിയമായി രൂപാന്തരപ്പെടുത്തുമ്പോള് ലഭിക്കുന്നത് 1,76,000 കി.വാ.മ. ഊര്ജമാണ്. ചില പരിതഃസ്ഥിതികളില് വിഘടനപ്രക്രിയ ശൃംഖലാക്രമത്തില് തുടര്ന്നുകൊണ്ടിരിക്കുന്നതുപോലെ ഹൈഡ്രജന് സംയോജനപ്രക്രിയ (Hydrogen fusion process) അനുകൂലമായ ചില പരിതഃസ്ഥിതികളില് തുടര്ന്നു നടക്കുന്നതാണ്. അണുകേന്ദ്രസംയോജനസാധ്യത അതില് പങ്കെടുക്കുന്ന അണുകേന്ദ്രങ്ങളുടെ ഗതികോര്ജത്തെ ആശ്രയിച്ചിരിക്കുന്നു. ഗതികോര്ജം കൂടുംതോറും സാധ്യത വര്ധിക്കുന്നു. 10 ലക്ഷം ഡിഗ്രി താപനില (temperature) ഉള്ളപ്പോള് ഡ്യൂട്ടറോണ് സംയോജനത്തിനുള്ള സംഭാവ്യത (probability) 10<sup>-15</sup> മുതല്10<sup |
>-12</sup> വരെയാണ്. 2 ഡ്യൂട്ടറോണുകള് തമ്മില് ഒരു സെക്കന്ഡില് 10<sup>10</sup> സംഘട്ടനങ്ങള് (collisions) നടക്കുന്നുവെന്നു സങ്കല്പിക്കുകയാണെങ്കില് ഒരു കി.ഗ്രാം ഘനഹൈഡ്രജനില് 3x10<sup>26</sup>ഡ്യൂട്ടറോണുകള് ഉള്ളതിനാല് വളരെ സംഘട്ടനങ്ങള് നടക്കാന് സാധ്യതയുണ്ട്. അതിനാല് 1 കി.ഗ്രാം ഡ്യൂട്ടറോണില്നിന്നു 100 കി.വാ.മ. ഊര്ജം ലഭിക്കുമെന്നു കണക്കാക്കാം. 50 മുതല് 60 വരെ ലക്ഷം ഡിഗ്രി താപനിലയുള്ളപ്പോള് ഒരു കി.ഗ്രാം ഡ്യൂട്ടറോണ് മുഴുവനും വെന്തുനീറി (burn out) 15 കോടി കി.വാ.മ. ഊര്ജം ഒരു സെക്കന്ഡിന്റെ ചെറിയൊരംശം സമയത്തില് മോചിപ്പിക്കപ്പെടുന്നതാണ്. | >-12</sup> വരെയാണ്. 2 ഡ്യൂട്ടറോണുകള് തമ്മില് ഒരു സെക്കന്ഡില് 10<sup>10</sup> സംഘട്ടനങ്ങള് (collisions) നടക്കുന്നുവെന്നു സങ്കല്പിക്കുകയാണെങ്കില് ഒരു കി.ഗ്രാം ഘനഹൈഡ്രജനില് 3x10<sup>26</sup>ഡ്യൂട്ടറോണുകള് ഉള്ളതിനാല് വളരെ സംഘട്ടനങ്ങള് നടക്കാന് സാധ്യതയുണ്ട്. അതിനാല് 1 കി.ഗ്രാം ഡ്യൂട്ടറോണില്നിന്നു 100 കി.വാ.മ. ഊര്ജം ലഭിക്കുമെന്നു കണക്കാക്കാം. 50 മുതല് 60 വരെ ലക്ഷം ഡിഗ്രി താപനിലയുള്ളപ്പോള് ഒരു കി.ഗ്രാം ഡ്യൂട്ടറോണ് മുഴുവനും വെന്തുനീറി (burn out) 15 കോടി കി.വാ.മ. ഊര്ജം ഒരു സെക്കന്ഡിന്റെ ചെറിയൊരംശം സമയത്തില് മോചിപ്പിക്കപ്പെടുന്നതാണ്. | ||
| വരി 262: | വരി 266: | ||
(പ്രൊഫ. എസ്. ഗോപാല മേനോന്) | (പ്രൊഫ. എസ്. ഗോപാല മേനോന്) | ||
| + | [[Category:ഭൗതികം-ന്യൂക്ളിയര്]] | ||
Current revision as of 08:47, 21 നവംബര് 2014
ഉള്ളടക്കം |
അണുകേന്ദ്രവിജ്ഞാനീയം
Nuclear Science
അണുകേന്ദ്രത്തില് അടങ്ങിയിരിക്കുന്ന ശക്തികളെയും ഉള്ളടക്കത്തെയും രസതന്ത്രപരവും ഭൗതികവുമായ വശങ്ങളിലൂടെ വിശകലനം ചെയ്യുന്ന ആധുനിക ശാസ്ത്രശാഖ. അണുകേന്ദ്രഭൗതികം, അണുകേന്ദ്രരസതന്ത്രം എന്നീ ഉള്പ്പിരിവുകള് ഇതിനുണ്ട്. അണു വിച്ഛേദിക്കപ്പെടാന് കഴിയാത്ത ഏറ്റവും ചെറിയ പദാര്ഥമാണെന്ന സങ്കല്പത്തിനു മാറ്റം വന്നതോടെ അണുവിജ്ഞാനീയമെന്നത് അണുകേന്ദ്രവിജ്ഞാനീയമായി. 2,500 വര്ഷങ്ങള്ക്കുമുമ്പ് ഗ്രീസിലും അതിനുമുമ്പുതന്നെ ഭാരതത്തിലും അണുവിനെക്കുറിച്ചുള്ള ശാസ്ത്രീയ ബോധമുണ്ടായിരുന്നു. നോ: അണു, അണുഭൌതികം
അണുകേന്ദ്രവിജ്ഞാനീയ വികാസത്തിന്റെ നാഴികക്കല്ലുകള്
1896-ല് ഹെന്റി ബെക്വറല് എന്ന ഫ്രഞ്ച് ശാസ്ത്രജ്ഞന് യുറേനിയം യൗഗികങ്ങളുടെ റേഡിയോ ആക്റ്റിവത (Radioactivity) കണ്ടുപിടിച്ചതോടുകൂടിയാണ് അണുകേന്ദ്രത്തെക്കുറിച്ചുള്ള അറിവ് വര്ധിച്ചത്. അതിനുശേഷം തുടരെയുള്ള കണ്ടുപിടിത്തങ്ങള് ഈ രംഗത്തുണ്ടായി. അവയില് പ്രധാനപ്പെട്ടവ താഴെ കുറിക്കുന്നു:
(1) യുറേനിയം ഖനിജങ്ങ(minerals)ളില്നിന്നു റേഡിയം വേര്തിരിച്ചെടുത്തത് - പിയര്ക്യൂറിയും മേരിക്യൂറിയും (1898);
(2) ദ്രവ്യമാനവും (mass) ഊര്ജവും (energy) തമ്മിലുള്ള ബന്ധം പ്രസ്താവിച്ചത് - ഐന്സ്റ്റൈന് (1905);
(3) ആല്ഫാ (α) കണങ്ങള് ഹീലിയത്തിന്റെ അണുകേന്ദ്രങ്ങളാണെന്നു പരീക്ഷണങ്ങള്കൊണ്ടു തെളിയിച്ചത് - റഥര്ഫോര്ഡും റോയിഡും (1909);
(4) കോസ്മിക കിരണങ്ങള് (cosmic rays) കണ്ടെത്തിയത് - ഹെസ്സ് (1910);
(5) ക്ളൗഡ്ചേംബര് (Cloud chamber) എന്ന ഉപകരണം നിര്മിച്ചത് - കോക്ക്രോഫ്റ്റ് വില്സണ് (1912);
(6) പരീക്ഷണശാലയില് അണുകേന്ദ്രമൂലകാന്തരണം (Nuclear transformation) ആദ്യമായി നടത്തിയത് - റഥര് ഫോര്ഡ് (1919);
(7) ദ്രവ്യമാന സ്പെക്ട്രോമീറ്റര് (Mass spectrometer) എന്ന ഉപകരണം നിര്മിച്ചത് - ആസ്റ്റണ് (1919);
(8) ദ്രവ്യകണങ്ങള്ക്കു തരംഗസ്വഭാവമുള്ളതായി വെളിപ്പെടുത്തിയത് - ദെ ബ്രോയെ (1924):
(9) ക്വാണ്ടം ബലതന്ത്രം (Quantum mechanics) എന്ന ഭൌതികശാസ്ത്രശാഖയുടെ ഉത്പത്തി-ഷോഡിംഗര്, ബാറണ്, ഹൈസന്ബര്ഗ്, ജോര്ഡന് എന്നിവരുടെ പ്രവര്ത്തനംമൂലം (1926);
(10) ഗൈഗര് മുള്ളര് കൌണ്ടര് (Geiger muller counter) എന്ന ഉപകരണത്തിന്റെ നിര്മാണം (1928);
(11) കൃത്രിമമായി ത്വരണം ചെയ്യപ്പെട്ട കണങ്ങള് (artifically accelerated particles) കൊണ്ട് അണുകേന്ദ്രമൂലകാന്തരണം നടത്തിയത് - കോക്ക്രോഫ്റ്റ് വില്സണ് (1930);
(12) സെക്ളോട്രോണ് (Cyclotron) എന്ന ഉപകരണം നിര്മിച്ചത് - ലോറന്സ് (1932);
(13) ന്യൂട്രോണ് കണ്ടുപിടിച്ചത് - ചാഡ്വിക് (1932).
(14) പോസിട്രോണ് കണ്ടുപിടിച്ചത് - ആന്ഡേഴ്സണ് (1932);
(15) അണുകേന്ദ്രം ന്യൂട്രോണുകളാലും പ്രോട്ടോണുകളാലും നിര്മിതമാണ് എന്നു നിര്ദേശിച്ചത് - ഹൈസന്ബര്ഗ് (1932);
(16) കൃത്രിമ റേഡിയോ ആക്റ്റിവത കണ്ടുപിടിച്ചത് - ജുലിയറ്റ് ക്യൂറിയും ഐറിന് ക്യൂറിയും (1934);
(17) മെസോണ് എന്ന കണത്തെ താത്ത്വികമായി വിഭാവനം ചെയ്തത് - യൂക്കാവാ (1935);
(18) അണുകേന്ദ്ര ഘടനയെക്കുറിച്ചുള്ള യൌഗിക-അണുകേന്ദ്രസിദ്ധാന്തം നിര്ദേശിച്ചത് - നീല്സ് ബോര് (1936);
(19) കോസ്മിക കിരണങ്ങളില് മ്യൂ (μ)- മെസോണ് കണ്ടെത്തിയത് - നെദര്മേയര്, ആന്ഡേഴ്സണ് (1937);
(20) അണുകേന്ദ്രകാന്തിക-ആഘൂര്ണത്തെ (Nuclear magnetic moment) കൃത്യമായി നിര്ണയിച്ചത് - റാബി (1938);
(21) അണുകേന്ദ്രവിഘടനം നിരീക്ഷിച്ചത് - ഹാന്, സ്റ്റ്രാസ്മാന് (1939);
(22) ആദ്യത്തെ അണുകേന്ദ്ര റിയാക്റ്റര് നിര്മിച്ചു പ്രവര്ത്തിപ്പിച്ചത് - ഫെര്മി (1942);
(23) പൈ (π) മെസോണ് എന്ന കണം കണ്ടുപിടിച്ചത് - സെസില് പൌവല്, സീസര് ലാറ്റസ്, ജൂസെപ്പെ ഒക്കിയാലിനി (1947);
(24) വി (V)-കണത്തിന്റെ കണ്ടുപിടിത്തം - റാച്ചസ്റ്റര് ബട്ലര് (1947);
(25) പരീക്ഷണശാലയില് കൃത്രിമമായി മെസോണുകള് നിര്മിച്ചത് - ഗാര്ഡ്നര്, ലാറ്റസ് (1948);
(26) അണുകേന്ദ്ര ഘടനയെക്കുറിച്ച് കവചസിദ്ധാന്തം (Shell theory) നിര്ദേശിച്ചത് - മേയര് ഹാക്സല് ജെന്സണ്, സൂയസ് (1949);
(27) താപ-അണുകേന്ദ്രീയ പ്രതിപ്രവര്ത്തനങ്ങ(thermo nuclear reactions)ളെക്കുറിച്ചുള്ള ഗവേഷണങ്ങള് - ഹൈഡ്രജന് ബോംബിന്റെ നിര്മാണം - 1956 മുതല്;
(28) താപ-അണു കേന്ദ്രീയ-പ്രതിപ്രവര്ത്തനോര്ജത്തെ (thermo-nuclear reaction energy) നിയന്ത്രിക്കാന് കഴിയുമെന്നും സമാധാനപരമായ ആവശ്യങ്ങള്ക്ക് ഉപയോഗിക്കാമെന്നും വെളിപ്പെടുത്തിയത് - സോവിയറ്റ് റഷ്യയിലെ കപിറ്റ്സ, പീറ്റര് ലെനിഡോവിച്ച് (ആഗ. 1970). നോ: അണുകേന്ദ്രം
ബന്ധന-ഊര്ജം
(Binding energy).
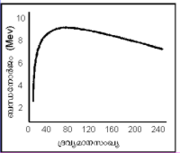
ഒരു അണുകേന്ദ്രത്തില് mp ദ്രവ്യമാനം വീതമുള്ള z പ്രോട്ടോണുകളും Mn വീതമുള്ള N ന്യൂട്രോണുകളും അടങ്ങിയിരിക്കുന്നു. Z പ്രോട്ടോണുകളുടെ ആകെ ദ്രവ്യമാനം Z ഹൈഡ്രജന് അണുകേന്ദ്രങ്ങളുടേതായിരിക്കും. അതിനാല് അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനം M=MH Z+Mn(A-Z) ആകേണ്ടതാണ്.ഇവിടെ MH ഹൈഡ്രജന് അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനവും A=Z+N- ആണ്. എന്നാല് അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനം (M) മേല്പറഞ്ഞതില് കുറവായിരിക്കും. ദ്രവ്യമാനവ്യത്യാസം, MHZ+Mn(A-Z)-M= Δ അതായത് Δ ദ്രവ്യനഷ്ടം സംഭവിക്കുന്നു. പ്രോട്ടോണുകളേയും ന്യൂട്രോണുകളേയും അതായത് ന്യൂക്ളിയോണുകളെ ബന്ധിക്കുന്ന ഊര്ജമാണിത്. അതിനാല് ബന്ധന-ഊര്ജം B=Δc2={MHZ+Mn(A-Z)-M}C2.ജൂള്സ്,e.v.എന്ന് ഇലക്ട്രോണ് വോള്ട്ടായും ഇത് കണക്കാക്കപ്പെടുന്നു. (c-പ്രകാശവേഗം). ഓരോ ന്യൂക്ലിയോണിനെയും ബന്ധിക്കുന്ന ശ.ശ. ഊര്ജം B=![\frac{[M_HZ+M_n(A-Z)-M]C^2}{A}](/images/math/d/5/a/d5ab4059ca5859b75401715d6ef447f0.png) ഇത് അണുകേന്ദ്രബലങ്ങളെ എതിര്ത്ത് ഓരോ ന്യൂക്ളിയോണിനെയും വേര്പെടുത്തി ദൂരെ മാറ്റുവാന് വേണ്ടിവരുന്ന പ്രവൃത്തിയെ ആണ് സൂചിപ്പിക്കുന്നത്. A-യെ അപേക്ഷിച്ച് B എപ്രകാരം മാറിവരുന്നു എന്നു ചിത്രത്തില്നിന്നു മനസ്സിലാക്കാം. ഏറ്റവും സ്ഥിരമായ അണുസമഭാരികം (isobar) (നോ: അണു) ആണ് കണക്കിലെടുത്തിട്ടുള്ളത്. A-50-നോടു സമീപിക്കുമ്പോള് B = 8.4 MeV കുറയുന്നില്ല. ചെറുതും വലുതും ദ്രവ്യമാനസംഖ്യയുള്ള അണുക്കള്ക്കു B ഇതിനേക്കാള് കുറവാണ്. വളരെ ചെറിയ ദ്രവ്യമാനസംഖ്യയുള്ള അണുക്കളുടെ B-ല് മുറതെറ്റിയ വ്യതിയാനമാണ് കാണുന്നത്. ഒരു ന്യൂക്ളിയോണിന്റെ ബന്ധന ഊര്ജം
ഇത് അണുകേന്ദ്രബലങ്ങളെ എതിര്ത്ത് ഓരോ ന്യൂക്ളിയോണിനെയും വേര്പെടുത്തി ദൂരെ മാറ്റുവാന് വേണ്ടിവരുന്ന പ്രവൃത്തിയെ ആണ് സൂചിപ്പിക്കുന്നത്. A-യെ അപേക്ഷിച്ച് B എപ്രകാരം മാറിവരുന്നു എന്നു ചിത്രത്തില്നിന്നു മനസ്സിലാക്കാം. ഏറ്റവും സ്ഥിരമായ അണുസമഭാരികം (isobar) (നോ: അണു) ആണ് കണക്കിലെടുത്തിട്ടുള്ളത്. A-50-നോടു സമീപിക്കുമ്പോള് B = 8.4 MeV കുറയുന്നില്ല. ചെറുതും വലുതും ദ്രവ്യമാനസംഖ്യയുള്ള അണുക്കള്ക്കു B ഇതിനേക്കാള് കുറവാണ്. വളരെ ചെറിയ ദ്രവ്യമാനസംഖ്യയുള്ള അണുക്കളുടെ B-ല് മുറതെറ്റിയ വ്യതിയാനമാണ് കാണുന്നത്. ഒരു ന്യൂക്ളിയോണിന്റെ ബന്ധന ഊര്ജം 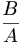 ആണ്.
ആണ്.
സ്വച്ഛന്ദ-അണുകേന്ദ്ര വിഘടനം
Spontaneous disintegration of the nucleus
അണുഭാരം വളരെ കൂടുതലുള്ള മൂലകങ്ങള് വികിരണത്തിനു (radiation) സ്വയം വിധേയമായി ഒന്നിനുപുറകെ മറ്റൊന്ന് എന്ന ക്രമത്തില് വിവിധ മൂലകങ്ങളായി രൂപം പ്രാപിച്ച് ഒടുവില് സ്ഥിരമൂലകമായ ഈയ (lead)ത്തില് എത്തിനില്ക്കുന്ന ഒരു പ്രത്യേകത പ്രദര്ശിപ്പിക്കുന്നുണ്ട്. സ്വാഭാവിക റേഡിയോആക്റ്റിവത (natural radioactivity) എന്നറിയപ്പെടുന്ന പ്രതിഭാസമാണിത്. ആല്ഫാ, ബീറ്റാ, ഗാമാ (α,β,γ) എന്നീ മൂന്നുതരം രശ്മികളാണ് വികിരണം ചെയ്യപ്പെടുന്നത്. ആല്ഫാ രശ്മികളായി പുറപ്പെടുന്നത് ഹീലിയം അണുകേന്ദ്രങ്ങള് തന്നെയാണ്. അവയ്ക്കു നിശ്ചിതതോതില് ഊര്ജവും ഇലക്ട്രോണിന്റെ രണ്ടിരട്ടി ധനചാര്ജുമുണ്ട്. ബീറ്റ രശ്മികളായി വരുന്നത് ഇലക്ട്രോണുകള് തന്നെയാണ്. അവയ്ക്ക് അവിച്ഛിന്ന-ഊര്ജ സ്പെക്ട്രം (continuous energy spectrum) ആണുള്ളത്. ഗാമാ ( γ)-രശ്മികള് എക്സ്-രശ്മികളെ(X-rays)ക്കാള് തരംഗനീളം കുറഞ്ഞ വിദ്യുത് കാന്തിക തരംഗങ്ങളാണ്. അവയുടെ ഊര്ജത്തിനു ചില നിശ്ചിതമായ അളവുകളുണ്ട്. അറിവില്പ്പെട്ട എല്ലാ റേഡിയോ ആക്റ്റിവ് രൂപാന്തരണങ്ങളിലും (Radioactive transformations) α അല്ലെങ്കില് β കണമാണ് ഉത്സര്ജിതമാകുന്നത്; ഒരു രൂപാന്തരണത്തില് ഏതെങ്കിലുമൊന്നുമാത്രം. A ദ്രവ്യമാനസംഖ്യയും Z അണുസംഖ്യയുമുള്ള ഒരു അണു α -കണത്തെ ഉത്സര്ജനം ചെയ്യുമ്പോള് നൂതനമായുണ്ടാകുന്ന അണുവിന്റെ ദ്രവ്യമാനസംഖ്യ (A-4)-ഉം അണുസംഖ്യ (Z- 2)-ഉം ആണ്. ഒരു β-കണമാണ് ഉത്സര്ജിതമാകുന്നതെങ്കില് പുതിയ അണുവിന്റെ ദ്രവ്യമാനസംഖ്യ A തന്നെയാണ്; അണുസംഖ്യ (Z + 1) ആകുകയും ചെയ്യും. ഇലക്ട്രോണിന്റെ ദ്രവ്യമാനം തുച്ഛമാണെന്നതാണ് ഇതിനു കാരണം. β-കണം ഉത്സര്ജിതമാകുമ്പോള് അണുകേന്ദ്രത്തിലെ ഒരു ന്യൂട്രോണ്, പ്രോട്ടോണ് ആയിത്തീര്ന്ന്, മൊത്തം ധനചാര്ജ് (Z + 1) ആയിത്തീരുന്നു.
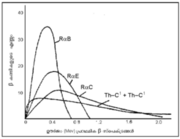
α,β,കണങ്ങള് വിപുലമായ ഗതികോര്ജ (Kinetic energy)ത്തോടുകൂടിയാണ് ഉത്സര്ജിക്കപ്പെടുന്നത്. കണം ഉത്സര്ജിതമായ ഉടനെ നൂതനമായി രൂപംകൊള്ളുന്ന അണുകേന്ദ്രം ഊര്ജസ്വലമായ നിലയിലാണ് വര്ത്തിക്കുന്നത്. താമസിയാതെ സാധാരണനിലയിലെത്തുമ്പോള് ഒരു γക്വാണ്ടം വമിക്കപ്പെടുന്നു. α-കണങ്ങള് ചില നിശ്ചിത ഊര്ജത്തോടെയാണ് പുറത്തുവരുന്നത്. ഉദാ. തോറിയം-C അണുക്കള് (Z= 83, A = 212) തോറിയം-C1 അണുക്കളായി (Z = 81, A = 208) രൂപാന്തരപ്പെടുമ്പോള് α-കണങ്ങള് E1= 6.201,E2 = 6.161, E3 = 5.873, E4 = 5.728, E5 = 5.709 എന്നീ MeV ഊര്ജത്തോടെയാണ് വമിക്കപ്പെടുന്നത്. αകണങ്ങള് തോറിയം-C അണുകേന്ദ്രങ്ങളില് മൂലാവസ്ഥയില് (ground state) നിന്നുയര്ന്ന് E4 -E2 = 0.04, E1-E2 = 0.328, E1-E4 = 0.473, E1-E5 = 0.492 MeV എന്ന ഊര്ജസ്തരങ്ങളില് വര്ത്തിക്കുന്നുവെന്നാണ് ഗാമോ (Gamow) എന്ന ശാസ്ത്രജ്ഞന് ഇതിനു നല്കിയ വ്യാഖ്യാനം. അണുകേന്ദ്രത്തിലുള്ള ഒരു α-കണം, E1 ഊര്ജസ്തര(energy level)ത്തില് നിന്നു മറ്റൊരു ഊര്ജസ്തരത്തിലേക്കു പതിക്കുമ്പോള് ഒരു γ-ക്വാണ്ടം ഉളവായി വമിക്കപ്പെടുന്നു. ഇങ്ങനെ 5 സ്തരങ്ങള് ഉള്ളതിനാല് 10 ജാതിയിലുള്ള γ-ക്വാണ്ടം ഉളവാകാന് സാധ്യതയുണ്ടെങ്കിലും 6 എണ്ണം മാത്രമാണ് നിരീക്ഷിക്കാന് കഴിഞ്ഞിട്ടുള്ളത്. ബാക്കി 4 എണ്ണം അവയുടെ ശക്തിക്കുറവിനാലോ ഏതോ അജ്ഞാതമായ നിര്ധാരണനിയമ(selection rule)ത്തിനു വിധേയമായി സംക്രമണങ്ങള് (transitions) നിരോധിച്ചതിനാലോ ആയിരിക്കാം നിരീക്ഷിക്കപ്പെടാന് കഴിയാതെപോകുന്നത്. റേഡിയം-C1, തോറിയം-C1 എന്നീ മൂലകങ്ങള് ശക്തമായ α-കണങ്ങള് വമിക്കാനിടവരുന്നത്, അണുകേന്ദ്രങ്ങള് വിവിധ ഉന്നത ക്വാണ്ടം നിലയില് വര്ത്തിക്കുന്നതുകൊണ്ടാണ് α-കണം വമിക്കാന്പോകുന്ന അണുകേന്ദ്രം അതിനു ജന്മംകൊടുത്ത പൂര്വവിഘടനത്തില് നിന്നു ലഭിച്ച ഊര്ജത്താല് ഉത്തേജിതാവസ്ഥയിലിരിക്കുകയാണ്. ഒരു γ-ക്വാണ്ടത്തെ വമിച്ച് താഴ്ന്ന ഒരു സ്തരത്തില് എത്തുന്നതിനുമുമ്പ് α-കണം പുറത്തുവരുന്നപക്ഷം അതു സാധാരണയില് കൂടുതലായ ഊര്ജത്തോടെ പ്രത്യക്ഷപ്പെടും. അധികപ്പറ്റായ ഊര്ജം ഉത്തേജിത അണുകേന്ദ്രത്തില്നിന്ന് അതു നേടുകയാണ് ചെയ്യുന്നത്. അണുകേന്ദ്രത്തില് നിശ്ചിതമായ ക്വാണ്ടരൂപത്തിലുള്ള ഊര്ജസ്തരങ്ങളുണ്ട്. β-കണങ്ങളുടെ ഊര്ജവിതരണം ചിത്രത്തില് കാണിച്ചിട്ടുള്ളതു പോലെയാണ്. അതുക്രമേണ ഉയര്ന്ന് അധികതമ(maximum)ത്തില് എത്തി പിന്നീട് പൂജ്യം ആയിത്തീരുന്നു. ആധുനികസിദ്ധാന്തപ്രകാരം കണങ്ങളുടെ അധികതമ-ഊര്ജം സമ്പൂര്ണവിഘടന-ഊര്ജം (total disintegration energy) തന്നെയാണ്. അണുകേന്ദ്രം നിശ്ചിതക്വാണ്ട-അവസ്ഥകളില് വര്ത്തിക്കുന്നുവെന്നതിന് α-കണങ്ങളുടെയും γ-ക്വാണ്ടത്തിന്റെയും ഊര്ജസ്പെക്ട്രം സ്ഥിരീകരണം നല്കുന്നു. പക്ഷേ, β-കണങ്ങള്ക്കു അവിച്ഛിന്ന-ഊര്ജവിതരണം (continuous energy distribution) ആണുള്ളത്. ഈ വ്യത്യാസം ഒരു പ്രശ്നമായി അവശേഷിക്കുന്നു. അണുകേന്ദ്രം ന്യൂട്രോണ് ക്വാണ്ട-അവസ്ഥയില്നിന്നു പ്രോട്ടോണ് ക്വാണ്ട-അവസ്ഥയിലേക്കു പരിവര്ത്തനം ചെയ്യുമ്പോഴാണ് β-കണം പുറത്തുവരുന്നത്. ഈ രണ്ടു ക്വാണ്ടം-അവസ്ഥകള് തമ്മിലുള്ള ഊര്ജ വ്യത്യാസമാണ് β-കണത്തിനു ലഭിക്കേണ്ട ഊര്ജം. എന്നാല് β-കണം പുറത്തുവരുന്നത് കുറഞ്ഞും കൂടിയുമുള്ള ഊര്ജത്തോടെയാണ്. β-കണത്തോടുകൂടി ന്യൂട്രിനോ എന്ന മറ്റൊരു കണംകൂടി വമിക്കുന്നുണ്ടെന്നും ആകെ ലഭ്യമാകുന്ന നിശ്ചിതവിഘടനോര്ജം β-കണവും ന്യൂട്രിനോയും തമ്മില് പങ്കുവച്ചെടുക്കുന്നുവെന്നുമാണ് പൗളി എന്ന ശാസ്ത്രജ്ഞന് ഇതിനു നല്കിയ സമാധാനം. β-കണത്തിനു അധികതമത്തില് ഊര്ജം ലഭിക്കുമ്പോള് ന്യൂട്രിനോയ്ക്ക് ഊര്ജമില്ലാതാകുന്നു; നേരെമറിച്ചും വരാം. ഈ ന്യൂട്രിനോയുടെ ദ്രവ്യമാനം നിസ്സാരമാണെങ്കിലും അതിന് ഊര്ജവും സംവേഗ(momentum)വും ഉണ്ട്.
ന്യൂക്ളിയാര് പൊട്ടന്ഷ്യല് പ്രാചീരം
Nuclear Pontential barrier
യുറേനിയം അണുകേന്ദ്രം α-കണങ്ങളെ പ്രകീര്ണനം ചെയ്യുമ്പോള് ശ്രദ്ധേയമായ ചില വസ്തുതകള് വെളിപ്പെടുന്നു. തോറിയം-C1-ല് (Th-C1) നിന്നു ലഭിക്കുന്ന 9 MeV ഊര്ജമുള്ളവ കൂളൂംനിയമത്തെ അതിലംഘിച്ച് യുറേനിയം അണുകേന്ദ്രത്തെ സമീപിക്കുന്നതിനു ശക്തിയുള്ളതല്ല, അണുകേന്ദ്രത്തില്നിന്നു 3 x 10-12 സെ.മീ. ദൂരം വരെയെങ്കിലും അണുകേന്ദ്രമണ്ഡലത്തില് α-കണത്തിന്റെ സ്ഥാനികോര്ജം (Pontential energy) കൂളും നിയമത്തിന് (Ur=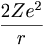 ) വിധേയമാണ്.
) വിധേയമാണ്.
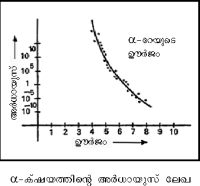
α-ന്യൂക്ലിയര് പൊട്ടന്ഷ്യല് പ്രാചീരം
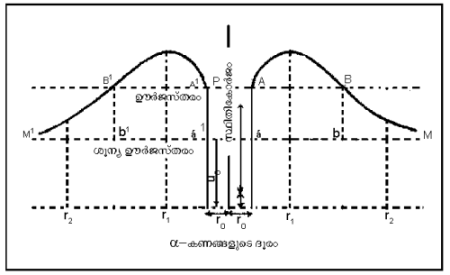
അണുകേന്ദ്രത്തില്നിന്നുള്ള ദൂരം (r) 3 x 10-12 സെ.മീ. ആണെങ്കില് സ്ഥാനികോര്ജം 9 MeVആയിരിക്കും. ദൂരംകുറയുംതോറും സ്ഥാനികോര്ജം വര്ധിച്ച് അധികതമത്തിലെത്തിക്കഴിഞ്ഞാല് പിന്നെ കൂളൂംനിയമം തകര്ന്നുപോകുന്നു. ഈ വികര്ഷണക്ഷമത (repulsive potential) α-കണത്തിന് അണുകേന്ദ്രത്തില് പ്രവേശനം നിരോധിക്കുന്നു. അത് ഒരു പൊട്ടന്ഷിയ പ്രാചീരമായി കണക്കാക്കാവുന്നതാണ്. അണുകേന്ദ്രത്തില്നിന്നും പുറത്തുവരുന്നതിനുമുമ്പ് അല്പസമയമെങ്കിലും α-കണം ആ രൂപത്തില് അണുകേന്ദ്രത്തില് ഉണ്ടായിരിക്കണം. അപ്പോള് α-കണവും റേഡിയോ ആക്റ്റിവ് അണുകേന്ദ്രവും തമ്മില് അകത്തും പുറത്തും ഉണ്ടാകുന്ന പരസ്പരക്രിയ (interaction) ആണ് ചിത്രത്തില് കാണിച്ചിട്ടുള്ള സ്ഥാനികോര്ജലേഖ(potential energy curve) സൂചിപ്പിക്കുന്നത്. r2 മുതല് r1 വരെ ലേഖ ഉയര്ന്നുകൊണ്ടിരിക്കുന്ന ഭാഗം α-കണം അണുകേന്ദ്രത്തെ സമീപിക്കുമ്പോള് വര്ധിച്ചുവരുന്ന വികര്ഷണത്തെ കാണിക്കുന്നു. അണുകേന്ദ്രത്തിന്റെ അകത്തും സമീപത്തും ഈ ലേഖയുടെ ആകൃതി കൃത്യമായി മനസ്സിലാക്കാന് കഴിഞ്ഞിട്ടില്ല. എന്നാല് വികര്ഷണക്ഷമതയ്ക്കുപകരം ഒരു ആകര്ഷണക്ഷമത V0, r0 എന്ന ദൂരംവരെ പ്രവര്ത്തിക്കുന്നു. ഈ ദൂരമാണ് അണുകേന്ദ്രത്തിന്റെ ഫലപ്രദമായ വ്യാസാര്ധം. α-കണം പുറത്തുവരുമ്പോള് അതിനുള്ള ഊര്ജം (Eα) തന്നെയാണ് അതിനകത്തുമുള്ളത്. α-കണത്തിന്റെ ഗതികോര്ജമായി അവശേഷിക്കുന്നത് ആകെയുള്ള Eα-യില്നിന്നു V0 കുറച്ചുകിട്ടുന്ന Eα-V0 ആണ്.
യുറേനിയം അണുകേന്ദ്രത്തെ സമീപിക്കുന്ന ഒരു α-കണം അഭിമുഖീകരിക്കുന്നത് 9 Mev സ്തരമുള്ള ഒരു പൊട്ടന്ഷിയ ഊര്ജപ്രാചീരമാണ്. എന്നാല് യുറേനിയം അണുകേന്ദ്രം വമിക്കുന്ന α-കണത്തിനു 4 Mev ഊര്ജമാണുള്ളത്. അകത്തും ഈ ഊര്ജംതന്നെയാണുണ്ടായിരിക്കേണ്ടത്. ഈ α-കണത്തിന് ഒരു തരംഗസ്വരൂപം കൂടിയുള്ളതുകൊണ്ടാണ് 4 MeV ഉള്ള α-കണം 9 MeV സ്തരത്തിലുള്ള പ്രാചീരം കടന്നു പുറത്തുവരുന്നത്. അതിന്റെ തരംഗനീളം ആണ് h 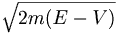 . ഇവിടെ, E ചിത്രത്തില് P A B നിരപ്പായി കാണിച്ചിട്ടുള്ള ആകെ ഊര്ജവും V സ്ഥിതികോര്ജവുമാണ്. കണം MBAC DC' A' B' M' രേഖയ്ക്കു മുകളിലാണ്; അതായത് പൊട്ടന്ഷ്യല് വെല്ലി(potential well)നകത്തോ പുറത്തോ ആയിരിക്കണം. Aa,Bb,aA'a',B'b' എന്നീ പരിധികള്ക്കകത്ത് E-യെക്കാള് കൂടുതലാണ് V. അപ്പോള് E-V ഋണാത്മകമാകയാല് തരംഗനീളം കല്പിതസംഖ്യ (imaginary number) ആയിരിക്കുന്നു. അതിന്റെ അര്ഥം തരംഗത്തിനു AC DC' A' എന്ന അതിര്ത്തിക്കുള്ളില് പൂര്ണപ്രതിഫലനം (total reflection) സംഭവിക്കുന്നു എന്നതാണ്. അണുവില് ഇലക്ട്രോണുകള് നിശ്ചിത ഊര്ജങ്ങളിലും ആവൃത്തി(frequency)കളിലും സ്ഥിതി ചെയ്യുന്നതുപോലെ അണുകേന്ദ്രത്തിനകത്ത് α-കണങ്ങള് ചില നിശ്ചിത ഊര്ജങ്ങളിലും ആവൃത്തികളിലും സ്ഥിതിചെയ്യുന്നുണ്ടാകണം. ചിത്രത്തില് AB,A'B' എന്നീ മേഖലകളില് തരംഗനീളം കല്പിതമാണെങ്കിലും തരംഗഫലനം (wave function) ψ=ψ0sin 2πrt വാസ്തവികം (real) ആണ്. തരംഗ-ആയാമം (wave amplitude) A-യിലോ A'-ലോ ശൂന്യമാകുന്നില്ലെങ്കിലും എക്സ്പൊണന്ഷ്യല് (exponential) ആയി കുറഞ്ഞ് B-യില് അഥവാ B'-ല് എത്തുമ്പോള് തുച്ഛമാകുന്നു എന്നല്ലാതെ പൂജ്യമാകുന്നില്ല. B അഥവാ B' തരണംചെയ്താല് തരംഗം വീണ്ടും വാസ്തവികമായിത്തീരുന്നു. ആയാമം കുറവുള്ള ഒരു തരംഗം അണുകേന്ദ്രത്തില്നിന്നു പുറത്ത്
. ഇവിടെ, E ചിത്രത്തില് P A B നിരപ്പായി കാണിച്ചിട്ടുള്ള ആകെ ഊര്ജവും V സ്ഥിതികോര്ജവുമാണ്. കണം MBAC DC' A' B' M' രേഖയ്ക്കു മുകളിലാണ്; അതായത് പൊട്ടന്ഷ്യല് വെല്ലി(potential well)നകത്തോ പുറത്തോ ആയിരിക്കണം. Aa,Bb,aA'a',B'b' എന്നീ പരിധികള്ക്കകത്ത് E-യെക്കാള് കൂടുതലാണ് V. അപ്പോള് E-V ഋണാത്മകമാകയാല് തരംഗനീളം കല്പിതസംഖ്യ (imaginary number) ആയിരിക്കുന്നു. അതിന്റെ അര്ഥം തരംഗത്തിനു AC DC' A' എന്ന അതിര്ത്തിക്കുള്ളില് പൂര്ണപ്രതിഫലനം (total reflection) സംഭവിക്കുന്നു എന്നതാണ്. അണുവില് ഇലക്ട്രോണുകള് നിശ്ചിത ഊര്ജങ്ങളിലും ആവൃത്തി(frequency)കളിലും സ്ഥിതി ചെയ്യുന്നതുപോലെ അണുകേന്ദ്രത്തിനകത്ത് α-കണങ്ങള് ചില നിശ്ചിത ഊര്ജങ്ങളിലും ആവൃത്തികളിലും സ്ഥിതിചെയ്യുന്നുണ്ടാകണം. ചിത്രത്തില് AB,A'B' എന്നീ മേഖലകളില് തരംഗനീളം കല്പിതമാണെങ്കിലും തരംഗഫലനം (wave function) ψ=ψ0sin 2πrt വാസ്തവികം (real) ആണ്. തരംഗ-ആയാമം (wave amplitude) A-യിലോ A'-ലോ ശൂന്യമാകുന്നില്ലെങ്കിലും എക്സ്പൊണന്ഷ്യല് (exponential) ആയി കുറഞ്ഞ് B-യില് അഥവാ B'-ല് എത്തുമ്പോള് തുച്ഛമാകുന്നു എന്നല്ലാതെ പൂജ്യമാകുന്നില്ല. B അഥവാ B' തരണംചെയ്താല് തരംഗം വീണ്ടും വാസ്തവികമായിത്തീരുന്നു. ആയാമം കുറവുള്ള ഒരു തരംഗം അണുകേന്ദ്രത്തില്നിന്നു പുറത്ത് 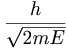 തരംഗനീളമുള്ള ഒരു ഗോളീയ തരംഗം (spherical wave) ജനിക്കുന്നു. ഒരു തരംഗം അണുകേന്ദ്രത്തിനകത്തുള്ള ഒരു തരംഗം ക്രമേണ ക്ഷയിക്കുന്നുവെന്നര്ഥം. α-കണം അണുകേന്ദ്രത്തില്നിന്നു രക്ഷപ്പെടാനുള്ള സാധ്യതയുണ്ടാകുന്നു.
തരംഗനീളമുള്ള ഒരു ഗോളീയ തരംഗം (spherical wave) ജനിക്കുന്നു. ഒരു തരംഗം അണുകേന്ദ്രത്തിനകത്തുള്ള ഒരു തരംഗം ക്രമേണ ക്ഷയിക്കുന്നുവെന്നര്ഥം. α-കണം അണുകേന്ദ്രത്തില്നിന്നു രക്ഷപ്പെടാനുള്ള സാധ്യതയുണ്ടാകുന്നു.
പ്രാചീരത്തിന്റെ ഉയരം കൂടുന്തോറും തരംഗസമൂഹം (wave packet) പുറത്തേക്ക് ഒഴുകുന്ന നിരക്കു ചുരുങ്ങുകയും അണുകേന്ദ്രത്തില്നിന്നു പുറത്തുവരുവാനുള്ള സാധ്യത കുറയുകയും ചെയ്യും.
അണുകേന്ദ്ര മാതൃകകള്
Nuclear models
ദ്രാവകതുള്ളി മാതൃക
Liquid drop model).
എല്ലാ അണുകേന്ദ്രങ്ങളിലും അണുകേന്ദ്രദ്രവ്യ(nuclear matter)ത്തിനു മിക്കവാറും ഒരേ സാന്ദ്രത (density) ആണ്. ഒരു ദ്രാവകത്തിന്റെ തുള്ളിക്കു വലിയ വ്യത്യാസമുണ്ടെങ്കിലും സാന്ദ്രതയ്ക്ക് വ്യത്യാസമില്ല. അതിനാല് അണുകേന്ദ്രത്തിന്റെ ഗുണങ്ങളെ ഒരു ദ്രാവകത്തിന്റെ തുള്ളിയായി താരതമ്യപ്പെടുത്തുന്നത് പ്രയോജനകരമായേക്കുമെന്ന് ബോര് (Bohr) കരുതി. അവ തമ്മില് പല സാദൃശ്യങ്ങളുമുണ്ട്: (1) ന്യൂക്ളിയോണുകള് തമ്മിലുള്ള സ്ഥിരബന്ധനോര്ജത്തിനു തുള്ളിയുടെ ബാഷ്പ-ലീനതാപ (latent heat of vapourisation)വുമായി സാമ്യമുണ്ട്; (2) തുള്ളിയുടെ ബാഷ്പനത്തിന് അണുകേന്ദ്രത്തിന്റെ റേഡിയോ ആക്റ്റിവതയുമായുള്ള സാമ്യം; (3) തുള്ളിക്കകത്തുള്ള തന്മാത്രകളുടെ താപീയ കമ്പന-ഊര്ജവും (thermal vibration energy) ന്യൂക്ളിയോണുകളുടെ ഊര്ജവും തമ്മില് സാമ്യമുണ്ട്; (4) ചെറിയ തുള്ളികള് ചേര്ന്ന് വലിയ തുള്ളിയായിത്തീരുന്നതുപോലെ, പതനകണങ്ങളെ (bombarding particles) സ്വീകരിച്ച് ഒരു സംയുക്ത അണുകേന്ദ്രം രൂപംകൊള്ളുന്നു.
ഒരു തുള്ളിക്കകത്തുള്ള തന്മാത്രകള് അവയുടെ ഏറ്റവും സമീപത്തുള്ള തന്മാത്രകളുടെ സ്വാധീനശക്തിക്കു മാത്രമേ വിധേയമായിരിക്കയുള്ളു. അതുപോലെ ന്യൂക്ളിയോണും ന്യൂക്ളിയോണും തമ്മിലുള്ള ബലങ്ങള്ക്കു ഹ്രസ്വപരാസമേയുള്ളു. തുള്ളിയുടെ പ്രതലത്തിലുള്ള തന്മാത്രകള് അകത്തുള്ളവയെപ്പോലെ ദൃഢമായ ബന്ധനത്തില് അല്ല സ്ഥിതിചെയ്യുന്നത്. അതുപോലെ അണുകേന്ദ്രത്തിന്റെ പ്രതലത്തിലെ ന്യൂക്ളിയോണുകള് അകത്തുള്ളവയെപ്പോലെ ദൃഢമായി ബന്ധപ്പെട്ടിരിക്കുന്നില്ല.
ഈ ആശയങ്ങളെല്ലാം കണക്കിലെടുത്ത് A,Z,M എന്നീ ഭൌതികവസ്തുതകള് (Physical data) ഉള്പ്പെടുത്തി AMz എന്ന അണുകേന്ദ്രത്തിന്റെ ദ്രവ്യമാനത്തെയും EB എന്ന ബന്ധനോര്ജ(binding energy)ത്തെയും ചേര്ത്തുള്ള ഒരു ആനുഭവികസൂത്രവാക്യം (empirical formula) രൂപപ്പെടുത്താന് സാധിച്ചു: AMz=Z MH+(A-Z)Mn-EB. ഇവിടെ MH,Mn എന്നിവ ക്രമത്തില് ഒരു ഹൈഡ്രജന് അണുവിന്റെയും ന്യൂട്രോണിന്റെയും ദ്രവ്യമാനമാണ്. അണുദ്രവ്യത്തെയും ബന്ധനോര്ജത്തെയും വളരെ സൂക്ഷ്മതയോടെ കണക്കാക്കിയെടുക്കാന് ഈ പരിഗണനയിലൂടെ സാധിക്കുന്നു. ഇതിനുപുറമേ 238U92 എന്ന അണു ഒരു α-ഉത്സര്ജകമാണെന്നുംβ-ഉത്സര്ജകമല്ലെന്നും സ്ഥാപിക്കാന് കഴിയും. ഉത്സര്ജനത്തിന്റെ ഊര്ജവും കണക്കാക്കാന് കഴിയുന്നു. ഒരു അണുകേന്ദ്രത്തിന്റെ വിഘടനാഭികഗുണങ്ങളെക്കുറിച്ചു പ്രവചിക്കാന് കഴിയുമെന്ന് ഇതില്നിന്നു മനസ്സിലാക്കാം. എങ്ങനെ അണുകേന്ദ്രവിഘടനം (nuclear fission) സംഭവിക്കുമെന്നു വിശദീകരിക്കുന്നതിലാണ് ദ്രാവകത്തുള്ളി മാതൃക വിജയിക്കുന്നത്. മന്ദഗതിയിലുള്ള ന്യൂട്രോണുകള് കൊണ്ട് 235U92 അണുവിന് വിഘടനം സംഭവിക്കുമെന്നും 238U92 അണുവിന് അതു സംഭവിക്കണമെങ്കില് അതിവേഗം ചലിക്കുന്ന ന്യൂട്രോണുകള് ആവശ്യമാണെന്നും സ്ഥാപിക്കാന് കഴിയും. ബന്ധനോര്ജസൂത്രം (binding energy formula) ഉപയോഗിച്ച് എല്ലാ അണുകേന്ദ്രങ്ങളുടെയും ബന്ധനോര്ജം (EB) കണ്ടുപിടിക്കാം. Z-നെ അപേക്ഷിച്ച് EB ഏതുപ്രകാരം പരിവര്ത്തിതമാകുന്നുവെന്ന് ലേഖ (curve) വരച്ച് അതില്നിന്നു മനസ്സിലാക്കാം. അതില്നിന്ന് അണുകേന്ദ്രങ്ങളുടെ സ്ഥിരത്വഗുണങ്ങളെ (stability properties)ക്കുറിച്ചും പ്രത്യേക സമഭാരിക (isobar) അണുക്കളുടെ βആക്റ്റിവതയെക്കുറിച്ചും അറിവുലഭിക്കുന്നതാണ്.
അണുകേന്ദ്ര കവചമാതൃക
Nuclear shell model
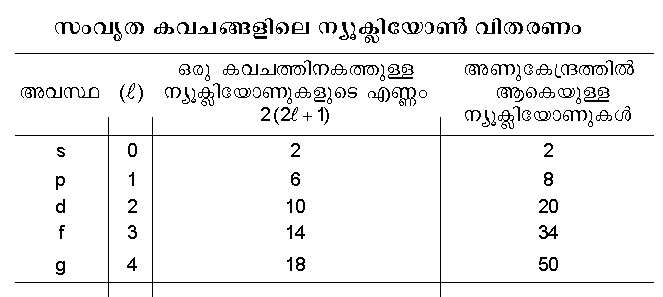
അണുവിലുള്ള ന്യൂട്രോണുകള്ക്കു വിജയപ്രദമായ ഒരു കവചമാതൃക (Shell model) ഉള്ളതായി സങ്കല്പിക്കാന് കഴിഞ്ഞിട്ടുണ്ട് (നോ: അണു). അതുപോലെ അണുകേന്ദ്രത്തില് ക്രമീകൃതവും ക്വാണ്ടം വ്യവസ്ഥയ്ക്കു വിധേയവുമായ അണുകേന്ദ്രകവചങ്ങളില് ന്യൂക്ളിയോണുകള് സ്ഥിതിചെയ്യുന്നുണ്ടാകാം. ഇവ തമ്മില് സാദൃശ്യം വളരെയേറെ ഉള്ളതിനാല് അണുകേന്ദ്രത്തിന്റെ ഗണിക്കപ്പെട്ട എല്ലാ ഗുണങ്ങളെയും പരിശോധിക്കേണ്ടിയിരിക്കുന്നു. ഉദാ. സ്ഥിരതാഗുണത്തെ പരിഗണിക്കുമ്പോള് 4n(n പൂര്ണസംഖ്യ) ന്യൂക്ളിയോണുകളുള്ള ന്യൂക്ളിയൈഡുകള് (Nucleids) താരതമ്യേന സ്ഥിരതയുള്ളവയാണ് എന്നു കാണാം. അണുകേന്ദ്രത്തില് Z, N എന്നിവയുടെ മൂല്യം 2, 8, 20, 28, 50, 82, 126 എന്നിവയാകുമ്പോള് അണുകേന്ദ്രം വളരെ സ്ഥിരതയുള്ളതായി കാണുന്നു. അവയെ മാന്ത്രികസംഖ്യകള് (magic figures) എന്നു വിളിച്ചുവരുന്നു. സംവൃതകവചങ്ങളെ (closed shells) ആണ് അവ സൂചിപ്പിക്കുന്നത്. കക്ഷീയ-സംവേഗം-ക്വാണ്ടംസംഖ്യക്ക് (orbital angular momentum quantum number:l) 0, 1, 2, 3 എന്നീ മൂല്യം നല്കിയാല് ന്യൂക്ളിയോണുകള് 2, 8, 20, 50, 82, 126 എന്നീ സംഖ്യകളിലെത്തിച്ചേര്ന്ന് സംവൃതകവചങ്ങള് രൂപപ്പെടുന്നു. എന്നാല് 50-ല് കൂടുതലുള്ള മാന്ത്രികസംഖ്യകള് ഈ സൂത്രം ഉപയോഗിച്ചു ലഭിക്കുന്നില്ല.
എന്നാല് ഓരോ ന്യൂക്ലിയോണിനും 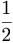
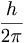 എന്ന ചക്രണകോണീയസംവേഗവും (spin angular momentum), lh/2 എന്ന കക്ഷീയ കോണീയസംവേഗവും (axial angular momentum) കല്പിക്കുകയാണെങ്കില് കോണീയസംവേഗം (l±1/2) h/2π =J h/2π എന്നു സിദ്ധിക്കും. ഒരു അണുകേന്ദ്രത്തില്, പൌളിയുടെ സിദ്ധാന്തപ്രകാരം (2J + 1) ന്യൂക്ളിയോണുകള്ക്കു സംപൂര്ണ കോണീയ സംവേഗം (Total angular momentum) ഉണ്ടാകാവുന്നതാണ്.
എന്ന ചക്രണകോണീയസംവേഗവും (spin angular momentum), lh/2 എന്ന കക്ഷീയ കോണീയസംവേഗവും (axial angular momentum) കല്പിക്കുകയാണെങ്കില് കോണീയസംവേഗം (l±1/2) h/2π =J h/2π എന്നു സിദ്ധിക്കും. ഒരു അണുകേന്ദ്രത്തില്, പൌളിയുടെ സിദ്ധാന്തപ്രകാരം (2J + 1) ന്യൂക്ളിയോണുകള്ക്കു സംപൂര്ണ കോണീയ സംവേഗം (Total angular momentum) ഉണ്ടാകാവുന്നതാണ്.
ഈ സങ്കല്പനങ്ങളെ അടിസ്ഥാനമാക്കി തുടരെയുള്ള അണുകേന്ദ്രോര്ജസ്തരങ്ങളില് ന്യൂക്ളിയോണുകളെ നിറച്ച് അണുകേന്ദ്രങ്ങള് ഓരോന്നായി ചെറുതുമുതല് വലുതുവരെ നിര്മിച്ചെടുക്കാന് കഴിയുമെന്നു മാത്രമല്ല, സംവൃതകവചങ്ങളെ സൂചിപ്പിക്കുന്ന എല്ലാ മാന്ത്രികസംഖ്യകളും കണ്ടെത്താന് കഴിയുകയും ചെയ്യും. ഇലക്ട്രോണികകവചങ്ങള്കൊണ്ട് അണുവിന്റെ ഘടനയെ ആവിഷ്കരിച്ച് മൂലകങ്ങളുടെ ആവര്ത്തകവര്ഗീകരണത്തെ (Periodic classification of elements) ബന്ധപ്പെടുത്തിയതുപോലെ, ന്യൂക്ളിയോണുകള് അടങ്ങിയ സംവൃതകവചങ്ങളാല് അണുകേന്ദ്രങ്ങള് നിര്മിതമായിരിക്കുന്നു എന്നു സങ്കല്പിക്കാന് കഴിയും.
കൃത്രിമ-അണുകേന്ദ്രവിഘടനം
Artificial nuclear disintegration
നൈട്രജന് അണുക്കളെ ശീഘ്രഗതിയുള്ള α-കണങ്ങള്കൊണ്ട് ആഘാതമേല്പിക്കുമ്പോള് പ്രോട്ടോണുകള് വമിക്കപ്പെടുമെന്നും അതോടുകൂടി ഓക്സിജന്റെ ഐസോടോപ്പ് (isotope) ആയ 17O8 അണുക്കള് സൃഷ്ടിക്കപ്പെടുമെന്നും 1919-ല് റഥര്ഫോര്ഡ് കണ്ടുപിടിച്ചു:
14N7+4He2→ (18H9)→17O8+ 1H1+Q
എന്ന സമീകരണംകൊണ്ട് ഈ പ്രതിപ്രവര്ത്തനം വിശദമാക്കാം. ഇതില് 18H9 അസ്ഥിരമായ യൌഗികാണുകേന്ദ്രമാണ്. Q അണുകേന്ദ്ര-പ്രതിപ്രവര്ത്തനോര്ജം (Nuclear reaction energy) ആണ്. ഇങ്ങനെയുള്ള പ്രതിപ്രവര്ത്തനത്തില് ഉള്പ്പെടുന്ന അണുകേന്ദ്രങ്ങളുടെയും കണങ്ങളുടെയും ദ്രവ്യമാനവും ഗതികോര്ജവും കണക്കിലെടുത്താല് M0+M1=M2+M3+ (E1+E2-E3)=M2+M3+Q എന്ന സമീകരണം സിദ്ധിക്കും. ഇവിടെ M0, M1, M2, M3 എന്നിവ യഥാക്രമം ആഘാതം ചെയ്യപ്പെട്ട അണുകേന്ദ്രത്തിന്റെയും ആഘാതം ഏല്പിച്ച കണത്തിന്റെയും ഉത്പന്ന-അണുകേന്ദ്രത്തിന്റെയും വമിക്കപ്പെട്ട കണത്തിന്റെയും ദ്രവ്യമാനമാണ്; E1, E2, E3 എന്നിവ യഥാക്രമം M1, M2, M3 എന്നിവയുടെ ഗതികോര്ജവും. ആഘാതമേറ്റ അണുകേന്ദ്രത്തിന്റെ ഗതികോര്ജം അവഗണിക്കാവുന്നതാണ്. Q ധനാത്മകമാണെങ്കില് പ്രതിപ്രവര്ത്തനം താപോന്മോചകവും (exothermic), ഋണാത്മകമാണെങ്കില് താപശോഷിതവും (endothermic), ആണ്. α-കണങ്ങളുടെ ആഘാതത്താല് ബോറോണ് (Boron) മുതല് കാല്ഷ്യം (Calcium) വരെയുള്ള മൂലകങ്ങള്ക്ക് (കാര്ബണും ഓക്സിജനും ഒഴികെ) മൂലകാന്തരണം (transmutation) സംഭവിക്കുന്നതാണ്. പുറത്തുപോകുന്ന കണം പ്രോട്ടോണ് ആയിരിക്കും. ഈ പ്രതിപ്രവര്ത്തനത്തെ α-p എന്നു പറയുന്നു.
10B5 +4He2→ (14N7)→13C6+ Q;Q=+4.4 MeV
105 മുതല് 107 വരെ α-കണങ്ങളുടെ ആഘാതമേല്ക്കുമ്പോഴാണ് ഒരു പ്രോട്ടോണ്കണം ഉണ്ടാകാന് സാധ്യതയുള്ളത്.
ആല്ഫാ-ന്യൂട്ടോണ് പ്രതിപ്രവര്ത്തനം. ഒരു അണുകേന്ദ്രം αകണത്തെ പിടിച്ചെടുക്കുമ്പോഴെല്ലാം പ്രോട്ടോണ്കണം ഉണ്ടാകണമെന്നില്ല; ഒരു ന്യൂട്രോണ്കണം ആകാനും സാധ്യതയുണ്ട്. ന്യൂട്രോണ്കണത്തെ ചാഡ്വിക് (chadwick) കണ്ടുപിടിച്ചതുതന്നെ, α-കണങ്ങള്കൊണ്ട് ബെരീലിയത്തെ (Beryllium) ആഘാതം ചെയ്തപ്പോഴാണ്.
9Be4 + 4He2 &rarr(13C6)→12C6 +1n0
പ്രോട്ടോണിന്റെ ആഘാതത്താല് സംഭവിക്കാവുന്ന മൂലകാന്തരണം (Transmutation by protons). ലിഥിയത്തെ പ്രോട്ടോണ്കണംകൊണ്ട് ആഘാതം ഏല്പിച്ചപ്പോള് ഹീലിയം കണങ്ങളുണ്ടായി. കോക്ക്രോഫ്ട്ടും വില്സണും ആണ് ഈ പരീക്ഷണം നടത്തിയത്. 0.1 മുതല് 0.7 Mev വരെ ഊര്ജമുള്ള പ്രോട്ടോണ്കണം അവര് ഉപയോഗിച്ചു.
11B5 + 1H1→ (12C6)→8Be4 +4He2
പ്രോട്ടോണ് കണങ്ങളുടെ ആഘാതത്താല് ന്യൂട്രോണുകള് ഉണ്ടാകുന്ന പ്രതിപ്രവര്ത്തനങ്ങളും ഉണ്ട്. p-n എന്നാണ് ഇവ അറിയപ്പെടുന്നത്.
പ്രോട്ടോണ്-ന്യൂട്രോണ് പ്രതിപ്രവര്ത്തനം. ഇത്തരം പ്രതിപ്രവര്ത്തനത്തില് ദ്രവ്യമാനത്തിനു വരുന്ന വ്യത്യാസം ഋണാത്മകമായതിനാല് ഊര്ജശോഷിതം (endoergic) ആയിരിക്കും.
11B5 + 1H1→ (12C6)→11C6 + 1n0
പ്രോട്രോണ്-ഗാമ പ്രതിപ്രവര്ത്തനം. ചില സന്ദര്ഭങ്ങളില് ആഘാതം ഏല്പിക്കുന്ന പ്രോട്ടോണിനെ ആഘാതം ഏല്ക്കുന്ന അണുകേന്ദ്രം പിടിച്ചെടുത്തുവെന്നു വരാം. അപ്പോള് ഉണ്ടാകുന്ന യൌഗിക-അണുകേന്ദ്രം അസ്ഥിരമാകയാല് γ-രശ്മി വികിരണം ചെയ്ത് സുസ്ഥിരത ലഭിക്കുന്നു.
7Li3 + 1H1→ (8Be4)→8Be4 + γ
പ്രോട്ടോണ്-ഡ്യൂട്ടറോണ് പ്രതിപ്രവര്ത്തനം.
9Be4+1H1→ (10B5)→8Be4+ 2H1
ഡ്യൂട്ടറോണ് -α-കണം പ്രതിപ്രവര്ത്തനം. ഈ പ്രതിപ്രവര്ത്തനം ഊര്ജമോചകമാണ്. 6Li3+2H1→ (8Al4)→4He2+ 4He2
ഡ്യൂട്ടറോണ്-പ്രോട്ടോണ് പ്രതിപ്രവര്ത്തനം. ഇതും ഒരു ഊര്ജോന്മോചക പ്രക്രിയയാണ്. 12C6+2H1→ (14N7)→13C6 +1H1
ഡ്യൂട്ടറോണ്-ന്യൂട്രോണ് പ്രതിപ്രവര്ത്തനം. ഉദാ.
12C6+2H1→ (14N7)→13N7 +1n0
തണുപ്പിച്ച് കട്ടയാക്കിയ ഘനജലത്തെ (heavy water) ഡ്യൂട്ടറോണ്കൊണ്ട് ആഘാതം ഏല്പിച്ചപ്പോള് ശ്രദ്ധേയമായ ചില പ്രതിപ്രവര്ത്തനങ്ങള് ഉണ്ടായി.
2H1+2H1→ (4He2)→3H1 +1H1
3H1 എന്നതും ഹൈഡ്രജന്റെ ഐസോടോപ് ആയ ട്രിഷ്യം (Tritium) ആണ്. 12 വര്ഷമാണ് ഇതിന്റെ അര്ധായുസ് (half_life).
ന്യൂട്രോണ്കൊണ്ടുള്ള മൂലകാന്തരണം. അണുകേന്ദ്രത്തെ തുളച്ചുകയറുന്നതിനുള്ള കഴിവ് ന്യൂട്രോണുകള്ക്കുള്ളതുകൊണ്ട് n-α, n-p, n-2n, n- γ എന്നീ പ്രതിപ്രവര്ത്തനങ്ങള് സംഭവിക്കാം.
ഫോട്ടോണ്കൊണ്ടുള്ള മൂലകാന്തരണം. കോസ്മിക രശ്മികളിലൂടെ വരുന്ന ഉന്നതോര്ജമുള്ള ഫോട്ടോണ്കൊണ്ടും അണുകേന്ദ്രങ്ങളെ വിഘടനം ചെയ്യാന് കഴിയും.
അണുകേന്ദ്രവിഘടനം
Nuclear fission
92-ല് കവിഞ്ഞ അണുസംഖ്യയുള്ള മൂലകങ്ങള് കൃത്രിമമായി സൃഷ്ടിക്കാന് പരിശ്രമിച്ചപ്പോള് കണ്ടുപിടിക്കപ്പെട്ട ഒരു പ്രതിഭാസമാണ് അണുകേന്ദ്ര വിഘടനം. ഈ പരീക്ഷണങ്ങളില് ന്യൂട്രോണ്-γ പ്രതിപ്രവര്ത്തനങ്ങളും അവയെത്തുടര്ന്നുള്ള ഉത്പന്ന-അണുകേന്ദ്ര(product nucleus)ത്തിന്റെβ-ക്ഷയ ( β-decay)വും ആണ് സംഭവിച്ചത്. നേരത്തെ നടത്തിയ പരീക്ഷണങ്ങളില് യുറേനിയത്തെ ന്യൂട്രോണുകള്കൊണ്ട് ആഘാതം ചെയ്യപ്പെടുകയാണുണ്ടായത്. ഈ പരീക്ഷണങ്ങളില് പാരയുറേനിയം (Trans-Urenium) ലഭിച്ചതുകൂടാതെ റേഡിയത്തിന്റെ β-റേഡിയോ ആക്റ്റീവ് ഐസോടോപ്പുകളും β-radio active isotopes) കൂടി കാണപ്പെട്ടു. മേല്പറഞ്ഞ ന്യൂക്ളിയൈഡിനു ക്ഷയം സംഭവിച്ചപ്പോള് ലഭിച്ച വ്യുത്പന്നങ്ങള് ആക്റ്റിനിയ(Actinum)ത്തിന്റെ ഐസോടോപ്പുകളാണോ എന്നും സംശയിച്ചു. എന്നാല് ഈ അനുമാനങ്ങള് മറ്റു ചില വസ്തുതകള് പരിഗണിച്ചപ്പോള് ശരിയല്ലെന്നറിഞ്ഞു. റേഡിയത്തിന്റെ ഐസോടോപ്പുകളാണെന്നു സംശയിച്ചത് വാസ്തവത്തില് ബേരിയത്തിന്റേതാണെന്നും ആക്റ്റിനിയത്തിന്റെ ഐസോടോപ്പുകളാണെന്ന് അനുമാനിച്ചതു യഥാര്ഥത്തില് ലന്ഥാനത്തിന്റേതാണെന്നും ഹാന് (Hahn), സ്റ്റ്രാസ്മാന് (Straussmann) എന്നീ ശാസ്ത്രജ്ഞന്മാര് പരീക്ഷണങ്ങള്വഴി തെളിയിച്ചു. യുറേനിയത്തില്നിന്നു 140La57, 139Ba56 എന്നീ ന്യൂക്ളിയൈഡുകള് ലഭിച്ചതുകൊണ്ട് ഏതോ അജ്ഞാതമായ അണുകേന്ദ്രപ്രതിപ്രവര്ത്തനം ആണ് അവിടെ നടന്നതെന്നും യുറേനിയം അണുകേന്ദ്രം രണ്ടായി പിളര്ന്നിരിക്കാമെന്നും അനുമാനിച്ചു. തുടര്ന്നുണ്ടായ പരീക്ഷണങ്ങള് സ്റ്റ്രോണ്ഷിയം (Strontium) (S = 31), യിട്രിയം (Yttrium) (Z = 39), ക്രിപ്ടോണ് (Krypton) (Z = 36), ക്സിനോണ് (Xenon) (Z = 54) എന്നീ മൂലകങ്ങളും ഐസോടോപ്പുകളും ഉത്പന്നങ്ങളില് കണ്ടെത്തി. കൂടാതെ ബ്രോമിന് (Bromine), മോളിബ്ഡനം (Molybdenum), റൂബീഡിയം (Rubedium), ആന്റിമണി (Antimony), അയഡിന് (Iodine) എന്നിവയുടെ അണുകേന്ദ്രങ്ങളും ഉള്ളതായി അറിഞ്ഞു. യുറേനിയം അണുകേന്ദ്രം രണ്ടായി വിഭജിക്കപ്പെട്ടിരിക്കണമെന്നു മനസ്സിലാക്കാം. ഈ പ്രതിഭാസത്തെയാണ് അണുകേന്ദ്രവിഘടനമെന്നു പറയുന്നത്. യുറേനിയം-235 (235U)-അണുകേന്ദ്രത്തെ വിഘടനം ചെയ്യാന് താപീയ ന്യൂട്രോണ് (Thermal neutron) മതിയാകും. (238U)-നെ വിഘടനം ചെയ്യാന് കൂടുതല് ഊര്ജമുള്ള ന്യൂട്രോണുകള് വേണം. യുറേനിയം അണുകേന്ദ്രം മാത്രമല്ല, അണുസംഖ്യ 200-ല് കൂടുതലുള്ള പല അണുകേന്ദ്രങ്ങളും വിഘടനത്തിനു വിധേയമാണ്. വിഘടനം നടക്കുന്നതിനു ന്യൂട്രോണ് കണങ്ങള് തന്നെ വേണമെന്നില്ല. ഫോട്ടോണുകള്, ഇലക്ട്രോണുകള്, മെസോണുകള്, പ്രോട്ടോണുകള്, ഡ്യൂട്ടറോണുകള്, α-കണങ്ങള് എന്നിവയുടെ പ്രചോദനത്താല് വിഘടനം സംഭവിക്കാം.
235U92 + 1n0 →(236U92)→ X + Y
ഇതു യുറേനിയം-235 അണുകേന്ദ്രത്തിന്റെ വിഘടനത്തെ കുറിക്കുന്നു. ഇതില് n എന്നതു താപീയ ന്യൂട്രോണും, x,y എന്നിവ പ്രാഥമിക വിഘടനോത്പന്നങ്ങളും (primary fission products) ആണ്. ചിത്രത്തില് വിഘടനോത്പന്നങ്ങളുടെ സാംഖ്യിക പ്രകൃതം (statistical nature) സൂചിപ്പിക്കുന്നു. അണുസംഖ്യയെ ആധാരമാക്കി വിഘടനോത്പന്നങ്ങളുടെ വിതരണം ഈ ചിത്രത്തില്നിന്നു മനസ്സിലാക്കാം. അണുസംഖ്യ 118 ആയാല് സമമിത വിഘടനം (Symmetric fission) വളരെ അപൂര്വമാണെന്നും (0.01ശ.മാ.) ഇത് ഏറ്റവും സംഭാവ്യമാകുന്നത് 96,140 എന്നീ അണുസംഖ്യയുള്ള ഖണ്ഡങ്ങള് ഉണ്ടാകുന്ന വിഘടനമാണെന്നും ചിത്രം സൂചിപ്പിക്കുന്നു. മധ്യത്തിലുള്ള അല്പതമത്തെ അടിസ്ഥാനമാക്കി ലേഖ (curve) സമമിതം (symmetrical) ആണെന്നും കാണാം. ഓരോ ഘനഖണ്ഡത്തിനും അനുരൂപമായ ലഘുഖണ്ഡവും ഉണ്ടായിരിക്കണം. രണ്ടു ഖണ്ഡങ്ങളും അസ്ഥിരമാണ്. പ്രാഥമിക ഖണ്ഡങ്ങള് ശൃംഖലാക്രമത്തില് (chain like) ക്ഷയിച്ച് ഒടുവില് സ്ഥിരമൂലകങ്ങളായി അവശേഷിക്കുന്നു. വിഘടനം കഴിഞ്ഞ ഉടനെ പ്രാഥമിക ഖണ്ഡങ്ങളില്നിന്നു ശ.ശ. 2.5 ന്യൂട്രോണുകള് വമിക്കപ്പെടുന്നതാണ്. അവയില് 99 ശ.മാ.വും 10-13 സെക്കന്ഡിനകം പ്രത്യക്ഷപ്പെടുന്നതിനാല് അവയെ ക്ഷണിക ന്യൂട്രോണ് (prompt neutron) എന്നു വിളിക്കുന്നു. ഏതാനും ന്യൂട്രോണുകള് അല്പം താമസിച്ചു പ്രത്യക്ഷപ്പെടുന്നു.
വിഘടനത്തില്നിന്നു മോചിപ്പിക്കപ്പെടുന്ന ഊര്ജം
വിഘടനപ്രക്രിയയില് വളരെ അധികം ഊര്ജം ഉടന്തന്നെ മോചിപ്പിക്കപ്പെടുന്നു. അല്പം ശേഷിക്കുന്നതുതന്നെ പ്രാഥമിക ഖണ്ഡങ്ങള് ക്ഷയിക്കുമ്പോള് മോചിപ്പിക്കപ്പെടുന്നു. ആകാശത്തിലാണ് വിഘടനം സംഭവിക്കുന്നതെങ്കില് ആകെ മോചിപ്പിക്കപ്പെടുന്ന ഊര്ജം വിഘടനഖണ്ഡങ്ങളുടെ ഗതികോര്ജമായി പ്രത്യക്ഷപ്പെടുന്നു. ഒരു വലിയ അവശോഷക(absorber)ത്തിലാണ് വിഘടനം സംഭവിക്കുന്നതെങ്കില് ആകെ മോചിപ്പിക്കപ്പെടുന്ന ഊര്ജം അവശോഷകത്തില് താപമായിത്തീരുന്നു. താപീയ ന്യൂട്രോണുകള്കൊണ്ടു നടക്കുന്ന വിഘടനത്തില് 120 മുതല് 180 വരെ MeVഊര്ജം മോചിപ്പിക്കപ്പെടുന്നുണ്ട്. ഇതു ഘനഅണുകേന്ദ്രത്തിനുള്ള ദ്രവ്യമാനത്തിന്റെ 0.1 ശ.മാ. ഊര്ജത്തിനു തുല്യമാണ്.
വിഘടനത്തിന്റെ ശ്രദ്ധാര്ഹമായ ഗുണങ്ങള് മനസ്സിലാക്കാന് കഴിഞ്ഞപ്പോള് അതിനെക്കുറിച്ചുള്ള ശാസ്ത്രീയ പഠനത്തില് താത്പര്യം വളരെ വര്ധിച്ചു. അണുകേന്ദ്രത്തിന്റെ ബിന്ദുമാതൃകയെ ആസ്പദമാക്കി ബോര്, വീലര് (Bohr,Wheeler) എന്നീ ശാസ്ത്രജ്ഞന്മാര്, വിഘടനത്തിന്റെ പല ഗുണങ്ങള്ക്കും തക്കതായ വിശദീകരണം നല്കി. പല അണുകേന്ദ്രങ്ങള്ക്കും സമമിത വിഘടനത്തിനു വേണ്ടിവരുന്ന ഉത്തേജനോര്ജ(activation energy) ത്തിന്റെ അളവ് അവര് നിര്ണയിച്ചു. ഘനഅണുകേന്ദ്രത്തിനു മന്ദഗതിയുള്ള ന്യൂട്രോണ് കൊണ്ടു വിഘടനം സംഭവിക്കാനുള്ള സാധ്യതയെപ്പറ്റിയും അവര് പഠനം നടത്തി. മൌലിക ദ്രവ്യമാനസൂത്രമുപയോഗിച്ചാണ് ഇവയെല്ലാം മനസ്സിലാക്കിയത്. താപീയ ന്യൂട്രോണുകള്ക്ക് 235U-നെ വിഘടനം ചെയ്യാന് കഴിയുമെന്നും 238U-നെ വിഘടനം ചെയ്യാന് അവയ്ക്കു സാധിക്കുന്നതല്ലെന്നും അവര് സ്പഷ്ടമാക്കി.
അണുകേന്ദ്രവിഘടനത്തിന്റെ അനുപ്രയോഗങ്ങള്
Applications of nuclear fission
യുറേനിയം-235 അണുകേന്ദ്രം ഒരു താപീയ ന്യൂട്രോണിനെ അവശോഷണം (absorb) ചെയ്യുമ്പോള് ശ.ശ. 2.5 ന്യൂട്രോണുകള് മോചിക്കപ്പെടുമെന്നതുകൊണ്ട് ഒരു സ്വയം പ്രവര്ത്തിത ശൃംഖലാപ്രതിപ്രവര്ത്തനം സംഭവിക്കാന് സാധ്യതയുണ്ടെന്നു തെളിയിക്കപ്പെട്ടു.
സാധാരണ യുറേനിയം ലോഹത്തില് 235U 140-ല് ഒരംശം മാത്രമാണുള്ളത്. ബാക്കിയുള്ളതില് ഭൂരിഭാഗവും 238U ആണ്. ഒരു ശൃംഖലാപ്രതിപ്രവര്ത്തനത്തില് വരണമെങ്കില് അടുത്ത തലമുറയില് ജനിക്കുന്ന ന്യൂട്രോണുകളുടെ എണ്ണം ഈ തലമുറയില് ഉള്ളതിനേക്കാള് കൂടുതലായിരിക്കണം. അതായത്, 100 ന്യൂട്രോണുകള് പ്രാരംഭവിഘടനത്തെ പ്രോത്സാഹിപ്പിക്കുന്നുവെങ്കില് അടുത്ത തലമുറയില് വിഘടനത്തിലേര്പ്പെടാന് കഴിവുള്ള 100-ല് കൂടുതല് ന്യൂട്രോണുകള് ഉണ്ടാകണം. അങ്ങനെയുണ്ടാകണമെങ്കില് വിഘടനപ്രക്രിയ അനുസ്യൂതമായി തുടരേണ്ടതാണ്.
സാധാരണ യുറേനിയം ഒരു മന്ദീകാരി(moderator)യില് ചിതറിവച്ചിരിക്കുന്നുവെന്നു വിചാരിക്കുക. പുനരുത്പാദനഗുണകം k= ηepf എന്നെഴുതാം. ഇതില് യുറേനിയം 235U അണുകേന്ദ്രം ഒരു താപീയ ന്യൂട്രോണിനെ അവശോഷണം ചെയ്യുമ്പോള് ഉത്പാദിപ്പിക്കപ്പെടുന്ന ന്യൂട്രോണുകളുടെ ശ.ശ. എണ്ണം ആണ് η. ശീഘ്രഗതിയുള്ള ഈ ന്യൂട്രോണുകള്ക്ക് ഉന്നത-ഊര്ജമുള്ളതുകൊണ്ട് 238U അണുകേന്ദ്രങ്ങളെ വിഘടനം ചെയ്യാനുള്ള കഴിവുണ്ടാകുന്നു; c ശീഘ്രവിഘടനഗുണകം (e > 1) ആണ്. മന്ദീകാരി (സാധാരണ ഉപയോഗിക്കുന്നതു ഗ്രാഫൈറ്റ് ആണ്) ന്യൂട്രോണുകളെ മന്ദഗതിയിലാക്കുമ്പോള് 238U അവയില് ചിലതിനെ അനുനാദാവശോഷണം (resonance absorption) കൊണ്ട് അകറ്റിക്കളയുന്നു. ഒടുവില് ലഭിക്കുന്ന താപീയന്യൂട്രോണുകളില് ഏതാനും എണ്ണത്തെ മന്ദീകാരിതന്നെ അവശോഷണം ചെയ്യുന്നു. ശേഷിക്കുന്ന അംശം f ആണ്. ഇതിനെ താപീയ-ഉപയോഗ ഗുണകം (thermal utilisation factor) എന്നു പറയുന്നു. റിയാക്റ്ററിന്റെ വലുപ്പം അപരിമിതമല്ലാത്തതിനാല് അതിന്റെ പ്രതലത്തില്നിന്നു ന്യൂട്രോണുകള് ചോര്ന്നുപോകാനിടയുണ്ട്. ഈ കാരണത്താല് പ്രതിപ്രവര്ത്തനം നടക്കണമെങ്കില് റിയാക്റ്ററിന് ഒരു ക്രാന്തിക വലുപ്പമോ (critical size) അതില് കൂടുതലോ ഉണ്ടായിരിക്കണം. അണു-ഊര്ജം അനുസ്യൂതമായി മോചിപ്പിക്കപ്പെടണമെങ്കില് k( =ηepf)-യുടെ മൂല്യം 1-നേക്കാള് വലുതായിരിക്കണം. k-യുടെ മൂല്യം 1-നേക്കാള് വലുതായിരിക്കുന്നവിധം റിയാക്റ്റര് സംവിധാനം ചെയ്യുന്നു. കാഡ്മിയം നിയന്ത്രണദണ്ഡുകള് (Cadmium control rods) ഉപയോഗിച്ച് ന്യൂട്രോണുകളെ അവശോഷണം ചെയ്ത് k-യുടെ മൂല്യം 1-ല് കുറവാക്കി വിഘടനപ്രതിപ്രവര്ത്തനത്തെ നിയന്ത്രിക്കാവുന്നതാണ്. ഇതുപോലെ ഒരു റിയാക്റ്റര് ഫെര്മി എന്ന ശാസ്ത്രജ്ഞനും സഹപ്രവര്ത്തകരും ആദ്യമായി സംവിധാനം ചെയ്തു. ഷിക്കാഗോ സര്വകലാശാലയില് 1942 ഡി. 2-ന് ആണ് ഇതുണ്ടായത്.
ശീഘ്രതയുള്ള വിഘടനപ്രതിപ്രവര്ത്തനം ആണ് അണുബോംബു സ്ഫോടനത്തില് സംഭവിക്കുന്നത്. അണുബോംബ് സ്ഫോടനം ചെയ്യുമ്പോള്, താത്ത്വികവശത്ത് k എന്ന ഗുണാങ്കം വളരെ വലുതാകുന്നു. ക്രാന്തികവലുപ്പത്തില് അല്പം കുറവുള്ളതും അകലെ സംവിധാനം ചെയ്തിട്ടുള്ളതുമായ രണ്ടു ശുദ്ധ യുറേനിയം-235 ലോഹക്കട്ടികള് പെട്ടെന്ന് അടുപ്പിച്ച് ആകെയുള്ള വലുപ്പം ക്രാന്തിക വലുപ്പത്തെക്കാള് കൂടുതലാക്കി വിഘടനപ്രതിപ്രവര്ത്തനം അതിവേഗത്തില് നടത്തി അണു-ഊര്ജം ഭീമമായ തോതില് മോചിപ്പിക്കുകയാണ് ചെയ്യുന്നത്. ഇതാണ് അണുബോംബ് പ്രവര്ത്തനത്തിലടങ്ങിയിരിക്കുന്ന തത്ത്വം. നോ: അണുബോംബ്
അണുകേന്ദ്രസംയോജനം
Nuclear fusion
ലഘു അണുകേന്ദ്രങ്ങളെ സംയോജിപ്പിച്ച് ദ്രവ്യമാനസംഖ്യ കൂടുതലുള്ള അണുകേന്ദ്രം സൃഷ്ടിക്കാവുന്നതാണ്. ഉദാ. ഓക്സിജന് അണുകേന്ദ്രങ്ങള് സംയോജിപ്പിച്ച് സള്ഫര് അണുകേന്ദ്രം സൃഷ്ടിക്കാം.
16O8 + 16O8→ 32S16
ഈ സംയോജനപ്രക്രിയയില് 32-31.982=0.018 amu ദ്രവ്യമാനം 18 MeV ഊര്ജമായി രൂപാന്തരപ്പെട്ട് മോചനം സംഭവിക്കുന്നതാണ്.
23Na11 + 22Ne10 →45Se21
എന്ന സമീകരണത്തിലടങ്ങിയ സംയോജനപ്രക്രിയ മറ്റൊരുദാഹരണമാണ്. മേല്പറഞ്ഞ അണുകേന്ദ്രങ്ങളെക്കാളും താരതമ്യേന ലഘുവായ ഡ്യൂട്ടറോണ് അണുകേന്ദ്രങ്ങള് കൂടുതല് സുഗമമായി സംയോജിപ്പിക്കാന് കഴിയും:
2D1 +2D1→ 4He2
ഇവിടെ ലഭിക്കുന്ന ഊര്ജം 24 MeV ആണ്. സോഡിയവും നിയോണും സംയോജിപ്പിച്ച് ഒരു amu ലഭിക്കുന്ന ഊര്ജത്തിന്റെ 11 മടങ്ങാണ് ഒരു amu-ന് ഡ്യൂട്ടറോണ് സംയോജിപ്പിച്ചു ലഭിക്കുന്ന ഊര്ജം. ഒരു ഗ്രാം 235U വിഘടനം ചെയ്തു ലഭിക്കുന്ന ഊര്ജം 22,000 കി.വാ.മ. ആയിരിക്കെ ഡ്യൂട്ടറോണുകള് സംയോജിപ്പിച്ച് ഹീലിയം അണുകേന്ദ്രമാക്കുമ്പോള് ലഭിക്കുന്ന ഊര്ജം 16,000 കി.വാ.മ. ആണ്. ഒരു ഗ്രാം ഹൈഡ്രജന് സംയോജിപ്പിച്ച് ഹീലിയമായി രൂപാന്തരപ്പെടുത്തുമ്പോള് ലഭിക്കുന്നത് 1,76,000 കി.വാ.മ. ഊര്ജമാണ്. ചില പരിതഃസ്ഥിതികളില് വിഘടനപ്രക്രിയ ശൃംഖലാക്രമത്തില് തുടര്ന്നുകൊണ്ടിരിക്കുന്നതുപോലെ ഹൈഡ്രജന് സംയോജനപ്രക്രിയ (Hydrogen fusion process) അനുകൂലമായ ചില പരിതഃസ്ഥിതികളില് തുടര്ന്നു നടക്കുന്നതാണ്. അണുകേന്ദ്രസംയോജനസാധ്യത അതില് പങ്കെടുക്കുന്ന അണുകേന്ദ്രങ്ങളുടെ ഗതികോര്ജത്തെ ആശ്രയിച്ചിരിക്കുന്നു. ഗതികോര്ജം കൂടുംതോറും സാധ്യത വര്ധിക്കുന്നു. 10 ലക്ഷം ഡിഗ്രി താപനില (temperature) ഉള്ളപ്പോള് ഡ്യൂട്ടറോണ് സംയോജനത്തിനുള്ള സംഭാവ്യത (probability) 10-15 മുതല്10-12 വരെയാണ്. 2 ഡ്യൂട്ടറോണുകള് തമ്മില് ഒരു സെക്കന്ഡില് 1010 സംഘട്ടനങ്ങള് (collisions) നടക്കുന്നുവെന്നു സങ്കല്പിക്കുകയാണെങ്കില് ഒരു കി.ഗ്രാം ഘനഹൈഡ്രജനില് 3x1026ഡ്യൂട്ടറോണുകള് ഉള്ളതിനാല് വളരെ സംഘട്ടനങ്ങള് നടക്കാന് സാധ്യതയുണ്ട്. അതിനാല് 1 കി.ഗ്രാം ഡ്യൂട്ടറോണില്നിന്നു 100 കി.വാ.മ. ഊര്ജം ലഭിക്കുമെന്നു കണക്കാക്കാം. 50 മുതല് 60 വരെ ലക്ഷം ഡിഗ്രി താപനിലയുള്ളപ്പോള് ഒരു കി.ഗ്രാം ഡ്യൂട്ടറോണ് മുഴുവനും വെന്തുനീറി (burn out) 15 കോടി കി.വാ.മ. ഊര്ജം ഒരു സെക്കന്ഡിന്റെ ചെറിയൊരംശം സമയത്തില് മോചിപ്പിക്കപ്പെടുന്നതാണ്.
വേറൊരു ഫലപ്രദമായ പ്രതിപ്രവര്ത്തനം ആണ്
1H1 + 7Le3→ 24He2
എന്നത്; ഇതില് ലഭിക്കുന്ന ഊര്ജം 17 Mev. ഇങ്ങനെ വളരെ ഉന്നതമായ താപനിലയുള്ളപ്പോള് നടക്കുന്ന അണുകേന്ദ്ര പ്രതിപ്രവര്ത്തനത്തെ താപ-അണുകേന്ദ്ര പ്രതിപ്രവര്ത്തനം (thermo nuclear reaction) എന്നു പറയുന്നു.
ഒരു അണുബോംബ് സ്ഫോടനം ചെയ്യുമ്പോള് ക്ഷണികസമയത്തിനകം താപനില ലക്ഷക്കണക്കിനു ഡിഗ്രി ഉയരുന്നു. അതോടെ മര്ദം ഒരു ച.സെ.മീ.-ല് 10 കോടി ടണ് ആയി വര്ധിക്കുകയും ചെയ്യും. ഈ പരിതഃസ്ഥിതികളില് ചുവടെ ചേര്ക്കുന്ന താപ-അണുകേന്ദ്രപ്രതിപ്രവര്ത്തനങ്ങള് വിജയപ്രദമായി നടക്കുന്നതാണ്.
2D1 + 1H1→ 3He2 + വികിരണം
3T1 + 2D1→ 4He2 + 1n0
3T1 എന്നത് ഹൈഡ്രജന്റെ ഐസോടോപ് ആയ ട്രിഷ്യം മൂലകമാണ്. രണ്ടാമത് എഴുതിയിരിക്കുന്ന പ്രതിപ്രവര്ത്തനം അതിവേഗത്തില് (10-6 സെ.) നടക്കുന്നതുകൊണ്ട് അതുഹൈഡ്രജന് ബോംബു നിര്മാണത്തിന്റെ അടിസ്ഥാനതത്ത്വമായിത്തീരുന്നു.
മേല് വിവരിച്ച താപ-അണുകേന്ദ്ര പ്രതിപ്രവര്ത്തനങ്ങള് ഏതുവിധത്തില് നിയന്ത്രിച്ച് അതില്നിന്നും ലഭിക്കുന്ന ഭീമമായ ഊര്ജം സമാധാനപരമായ ആവശ്യങ്ങള്ക്കു വിനിയോഗിക്കാമെന്ന പ്രശ്നത്തെക്കുറിച്ചു നിരന്തരമായ ഗവേഷണങ്ങള് നടന്നുകൊണ്ടിരിക്കുകയാണ്. ഇതിനു വിജയകരമായ ഒരു നിവൃത്തിമാര്ഗം കണ്ടെത്തിയെന്ന് 1970 ആഗ.-ല് സോവിയറ്റ് യൂണിയന് പ്രഖ്യാപിക്കയുണ്ടായി. താപ-അണുകേന്ദ്ര പ്രതിപ്രവര്ത്തനം തുടങ്ങത്തക്കവിധത്തില് ഹൈഡ്രജന്റെ താപവും ഘനത്വവും ഉയര്ത്താനും അതേനിലയില് തുടരാനും ആവശ്യമായ ഉപകരണങ്ങള് നിര്മിക്കാന് സാധിച്ചിട്ടുണ്ട്. ഒരു നവീന അധികതമ ആവൃത്തി വൈദ്യുതീജനകം (high frequency current generator) ഉപയോഗിച്ച് ഹൈഡ്രജന്റെ താപനില 10 ലക്ഷം ഡിഗ്രിവരെ ഉയര്ത്തിയെന്നു പറയുന്നു. താപ-അണുകേന്ദ്ര പ്രതിപ്രവര്ത്തനം നിയന്ത്രിതമായി നടത്തുന്നതിനുള്ള ഗവേഷണങ്ങള് തുടരുകയാണ്. ഉയര്ന്ന താപനിലയിലുള്ള ഡ്യുറ്റീറിയം പ്ളാസ്മയെ ഒരു ചെറിയ വ്യാപ്തത്തിനകത്ത് ഒതുക്കി നിര്ത്തുന്നതിനുള്ള ഒരു സംവിധാനമാണ് ടോക്കമാക്ക് (Toramak). കാന്തികമണ്ഡലങ്ങള് ഉപയോഗിച്ചാണ് ഇത് സാധ്യമാക്കുന്നത്. അതിതീവ്രതയുള്ള ലേസര് ഉപയോഗിച്ചും പരീക്ഷണങ്ങള് നടക്കുകയാണ്. ഇങ്ങനെ പ്ളാസ്മയെ നിയന്ത്രിച്ച് നിര്ത്തിയാല് അണുകേന്ദ്രസംയോജനം സാധ്യമാകും.
സംയോജന പ്രതിപ്രവര്ത്തനത്തിന്റെ മേന്മകള്
റേഡിയോ ആക്റ്റിവ് ദ്രവ്യങ്ങള് ഉപയോഗിക്കേണ്ടിവരുന്നില്ല; (2) ഇന്ധനമായി ഉപയോഗിക്കുന്ന ദ്രവ്യം സുലഭമായി ലഭിക്കുന്ന ഹൈഡ്രജന് തന്നെയാണ്. പ്രതിപ്രവര്ത്തനത്തിന്റെ ഫലമായി അവശേഷിക്കുന്ന ദ്രവ്യം വളരെ ഉപയോഗപ്രദമായ ഹീലിയമാണ്; (3) അണുറിയാക്റ്ററിന്റെ പ്രവര്ത്തനത്തില് നേരിടുന്ന പ്രശ്നങ്ങള്: (a) ഇന്ധനദ്രവ്യത്തിന്റെ ഭീമമായ വില; (b) ദ്രവ്യം തയ്യാറാക്കിയെടുക്കാനുള്ള വിഷമങ്ങളും ചെലവും; (c) റേഡിയോ ആക്റ്റീവ് അവശിഷ്ടങ്ങളെ മാറ്റിക്കളയാനുള്ള ബുദ്ധിമുട്ടുകള്. ഈ പ്രശ്നങ്ങള് അണുകേന്ദ്ര സംയോജന പദ്ധതിയെ അഭിമുഖീകരിക്കുന്നില്ല.
(പ്രൊഫ. എസ്. ഗോപാല മേനോന്)