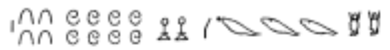This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
അക്കങ്ങള്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→അക്കങ്ങള്) |
|||
| (ഇടക്കുള്ള 48 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 1: | വരി 1: | ||
| - | = | + | = അക്കങ്ങള് = |
| | ||
Numerals | Numerals | ||
| വരി 5: | വരി 5: | ||
സംഖ്യകള് രേഖപ്പെടുത്തുന്നതിനുള്ള ചിഹ്നങ്ങള്. അതിപ്രാചീന കാലങ്ങളില്തന്നെ ഒരു ജീവിതാവശ്യമെന്ന നിലയില് മനുഷ്യന് എണ്ണാന് പഠിച്ചു. പിന്നെയും വളരെക്കാലം കഴിഞ്ഞിട്ടാണ് അക്കങ്ങള് ഉപയോഗിക്കാന് തുടങ്ങിയത്. എണ്ണം രേഖപ്പെടുത്താന് കല്ലും കമ്പും ഒരുപക്ഷേ അവന് ഉപയോഗിച്ചിരിക്കാം. പ്രാചീന രേഖകളനുസരിച്ച് കല്ലിലോ, വടിയിലോ അടയാളപ്പെടുത്തിയാണ് അക്കം എഴുതിയിരുന്നതെന്ന് കാണാം. അക്കം എഴുതേണ്ട ആവശ്യംതന്നെ അന്നുണ്ടായിരുന്നില്ല. സാധനങ്ങള് പരസ്പരം കൈമാറി ആവശ്യം നിറവേറ്റുന്ന വിനിമയ (Barter) സമ്പ്രദായമായിരുന്നു നിലവിലിരുന്നത്. ഏതാനും ശബ്ദങ്ങള് പുറപ്പെടുവിച്ച് എണ്ണം കുറിക്കുന്ന സമ്പ്രദായം വന്നതിനുശേഷമാകാം എഴുത്തുതുടങ്ങിയത്. ചെറിയ എണ്ണങ്ങള് സൂചിപ്പിക്കാന് ശബ്ദത്തിലൂടെ എളുപ്പത്തില് സാധിച്ചെങ്കിലും വലിയ എണ്ണങ്ങള് ആവശ്യമായി വന്നപ്പോള് എഴുതിവയ്ക്കാതെ നിവൃത്തിയില്ലാതായി. | സംഖ്യകള് രേഖപ്പെടുത്തുന്നതിനുള്ള ചിഹ്നങ്ങള്. അതിപ്രാചീന കാലങ്ങളില്തന്നെ ഒരു ജീവിതാവശ്യമെന്ന നിലയില് മനുഷ്യന് എണ്ണാന് പഠിച്ചു. പിന്നെയും വളരെക്കാലം കഴിഞ്ഞിട്ടാണ് അക്കങ്ങള് ഉപയോഗിക്കാന് തുടങ്ങിയത്. എണ്ണം രേഖപ്പെടുത്താന് കല്ലും കമ്പും ഒരുപക്ഷേ അവന് ഉപയോഗിച്ചിരിക്കാം. പ്രാചീന രേഖകളനുസരിച്ച് കല്ലിലോ, വടിയിലോ അടയാളപ്പെടുത്തിയാണ് അക്കം എഴുതിയിരുന്നതെന്ന് കാണാം. അക്കം എഴുതേണ്ട ആവശ്യംതന്നെ അന്നുണ്ടായിരുന്നില്ല. സാധനങ്ങള് പരസ്പരം കൈമാറി ആവശ്യം നിറവേറ്റുന്ന വിനിമയ (Barter) സമ്പ്രദായമായിരുന്നു നിലവിലിരുന്നത്. ഏതാനും ശബ്ദങ്ങള് പുറപ്പെടുവിച്ച് എണ്ണം കുറിക്കുന്ന സമ്പ്രദായം വന്നതിനുശേഷമാകാം എഴുത്തുതുടങ്ങിയത്. ചെറിയ എണ്ണങ്ങള് സൂചിപ്പിക്കാന് ശബ്ദത്തിലൂടെ എളുപ്പത്തില് സാധിച്ചെങ്കിലും വലിയ എണ്ണങ്ങള് ആവശ്യമായി വന്നപ്പോള് എഴുതിവയ്ക്കാതെ നിവൃത്തിയില്ലാതായി. | ||
| - | ചരിത്രം. ഈജിപ്ത്, ക്രീറ്റ്, സുമേറിയ, ഇന്ത്യ, ചൈന എന്നിവിടങ്ങളിലാണ് അക്കമെഴുത്ത് ആരംഭിച്ചത്. ഈജിപ്തിലും ക്രീറ്റിലും സുമേറിയയിലും മറ്റും ചിത്രലിപികള് ഉപയോഗിച്ചിരുന്നതായി പ്രാചീന രേഖകള് തെളിയിക്കുന്നു. ഏകദേശം ബി.സി. 3400-ല് ഈജിപ്തിലും 3000-ല് സുമേറിയയിലും 1200-ല് ക്രീറ്റിലും ഒന്ന്, പത്ത് എന്നിവ യഥാക്രമം | + | '''ചരിത്രം'''. ഈജിപ്ത്, ക്രീറ്റ്, സുമേറിയ, ഇന്ത്യ, ചൈന എന്നിവിടങ്ങളിലാണ് അക്കമെഴുത്ത് ആരംഭിച്ചത്. ഈജിപ്തിലും ക്രീറ്റിലും സുമേറിയയിലും മറ്റും ചിത്രലിപികള് ഉപയോഗിച്ചിരുന്നതായി പ്രാചീന രേഖകള് തെളിയിക്കുന്നു. ഏകദേശം ബി.സി. 3400-ല് ഈജിപ്തിലും 3000-ല് സുമേറിയയിലും 1200-ല് ക്രീറ്റിലും ഒന്ന്, പത്ത് എന്നിവ യഥാക്രമം [[Image:pno.22 .chrithram1.png]] എന്നീ രൂപത്തിലെഴുതിയിരുന്നു. |
പത്ത് അടിസ്ഥാനമാക്കിക്കൊണ്ടുള്ള അക്കങ്ങള്ക്കാണ് ഏറ്റവും പഴക്കമുള്ളത്. ഒരുപക്ഷേ മനുഷ്യന്റെ കൈവിരലുകളുടെ എണ്ണമായതിനാലാവാം പത്തിന് ഈ പ്രാധാന്യം വന്നത്. പത്ത് അടിസ്ഥാനമാക്കിയാണ് ഇംഗ്ളീഷില് എണ്ണങ്ങള്ക്കു പേരുകള് വന്നിട്ടുള്ളത്. പത്തു കൂടാത്ത മറ്റു സംഖ്യകളും ഉപയോഗിക്കാറുണ്ട്. ആസ്റ്റ്രേലിയയിലെ അതിപ്രാചീന വര്ഗക്കാരും ന്യൂഗിനിയുടെ പരിസരങ്ങളിലും റ്റോറസ് പ്രദേശത്തും ചില പാപ്പുവന് (papuan) ഭാഷക്കാരും ആഫ്രിക്കന് പിഗ്മികളും അനവധി തെക്കെ | പത്ത് അടിസ്ഥാനമാക്കിക്കൊണ്ടുള്ള അക്കങ്ങള്ക്കാണ് ഏറ്റവും പഴക്കമുള്ളത്. ഒരുപക്ഷേ മനുഷ്യന്റെ കൈവിരലുകളുടെ എണ്ണമായതിനാലാവാം പത്തിന് ഈ പ്രാധാന്യം വന്നത്. പത്ത് അടിസ്ഥാനമാക്കിയാണ് ഇംഗ്ളീഷില് എണ്ണങ്ങള്ക്കു പേരുകള് വന്നിട്ടുള്ളത്. പത്തു കൂടാത്ത മറ്റു സംഖ്യകളും ഉപയോഗിക്കാറുണ്ട്. ആസ്റ്റ്രേലിയയിലെ അതിപ്രാചീന വര്ഗക്കാരും ന്യൂഗിനിയുടെ പരിസരങ്ങളിലും റ്റോറസ് പ്രദേശത്തും ചില പാപ്പുവന് (papuan) ഭാഷക്കാരും ആഫ്രിക്കന് പിഗ്മികളും അനവധി തെക്കെ | ||
അമേരിക്കന് വര്ഗക്കാരും 'രണ്ട്' ആണ് ആധാരമായി സ്വീകരിച്ചത്. ടൈറാഡെല് ഫ്യൂഗോ വര്ഗക്കാരും തെക്കെ അമേരിക്കന് വന്കരയിലുള്ളവരും മൂന്ന്, നാല് എന്നിവയെ ആധാരമാക്കി എണ്ണം കുറിച്ചിരുന്നു. അഞ്ച് വളരെ പ്രാചീന കാലത്തുതന്നെ സ്വീകൃതമായിരുന്നു. തെക്കേ അമേരിക്കയിലെ ഒരു ആരാവാക്കന് ഭാഷയായ സാരാവെക്കിയില് മാത്രമാണ് ഇന്നും 'അഞ്ച്' ആധാരമായി ഉപയോഗിച്ചു കാണുന്നത്. മറ്റു ചിലേടത്ത് 'പത്തും' 'ഇരുപതും' ആധാരമായി സ്വീകരിച്ചുകാണുന്നു. ആഫ്രിക്കയുടെ വടക്കുപടിഞ്ഞാറന് പ്രദേശങ്ങളില് ആറും പന്ത്രണ്ടും പ്രയോഗിച്ചിരിക്കുന്നതുകാണാം. മെക്സിക്കോ, മധ്യാഫ്രിക്ക എന്നിവിടങ്ങളൊഴിച്ചാല് മറ്റു മിക്ക രാജ്യങ്ങളിലും ദശസമ്പ്രദായം സ്വീകരിച്ചിരുന്നു. എന്നാലും ദ്വാദശം (12), ജോടി (2) എന്നീ പ്രയോഗങ്ങളിലൂടെ 10 അല്ലാത്ത അടിസ്ഥാനങ്ങളും നടപ്പിലുണ്ടായിരുന്നു എന്നു വ്യക്തമാണ്. കോണങ്ങള് അളക്കുമ്പോള് ആധാരമായി 60 സ്വീകരിക്കാറുണ്ട്. | അമേരിക്കന് വര്ഗക്കാരും 'രണ്ട്' ആണ് ആധാരമായി സ്വീകരിച്ചത്. ടൈറാഡെല് ഫ്യൂഗോ വര്ഗക്കാരും തെക്കെ അമേരിക്കന് വന്കരയിലുള്ളവരും മൂന്ന്, നാല് എന്നിവയെ ആധാരമാക്കി എണ്ണം കുറിച്ചിരുന്നു. അഞ്ച് വളരെ പ്രാചീന കാലത്തുതന്നെ സ്വീകൃതമായിരുന്നു. തെക്കേ അമേരിക്കയിലെ ഒരു ആരാവാക്കന് ഭാഷയായ സാരാവെക്കിയില് മാത്രമാണ് ഇന്നും 'അഞ്ച്' ആധാരമായി ഉപയോഗിച്ചു കാണുന്നത്. മറ്റു ചിലേടത്ത് 'പത്തും' 'ഇരുപതും' ആധാരമായി സ്വീകരിച്ചുകാണുന്നു. ആഫ്രിക്കയുടെ വടക്കുപടിഞ്ഞാറന് പ്രദേശങ്ങളില് ആറും പന്ത്രണ്ടും പ്രയോഗിച്ചിരിക്കുന്നതുകാണാം. മെക്സിക്കോ, മധ്യാഫ്രിക്ക എന്നിവിടങ്ങളൊഴിച്ചാല് മറ്റു മിക്ക രാജ്യങ്ങളിലും ദശസമ്പ്രദായം സ്വീകരിച്ചിരുന്നു. എന്നാലും ദ്വാദശം (12), ജോടി (2) എന്നീ പ്രയോഗങ്ങളിലൂടെ 10 അല്ലാത്ത അടിസ്ഥാനങ്ങളും നടപ്പിലുണ്ടായിരുന്നു എന്നു വ്യക്തമാണ്. കോണങ്ങള് അളക്കുമ്പോള് ആധാരമായി 60 സ്വീകരിക്കാറുണ്ട്. | ||
| - | അക്കമെഴുത്ത്. പ്രാകൃത സമ്പ്രദായത്തില് I,II,III | + | '''അക്കമെഴുത്ത്'''. പ്രാകൃത സമ്പ്രദായത്തില് I, II, III, ≡ എന്നോ --, =, .., എന്നോ ആയിരിക്കണം അക്കങ്ങള് പ്രയോഗിച്ചിരുന്നത്. സൈബീരിയയിലെ യുക്കാഗിരന്മാര് ഒന്ന്, രണ്ട്, മൂന്ന്, മൂന്നും ഒന്നും, അഞ്ച്, രണ്ടുമൂന്ന്, രണ്ടു മൂന്നും ഒന്നും, രണ്ടുമൂന്നും രണ്ടും, ഒന്നൊഴികെ പത്ത്, പത്ത് എന്നിങ്ങനെയാണ് എണ്ണിയിരുന്നത്. എളുപ്പമായ രീതിയില് ഗ്രൂപ്പ് ചെയ്ത് അക്കങ്ങളെഴുതുന്ന രീതിയാണ് റോമക്കാരുടേത്. ഉദാ. 19-ന് XIX ഈജിപ്തില് ശിലാലിഖിതങ്ങളിലെ ചിത്രമെഴുത്തുകളിലാണ് ഈ സമ്പ്രദായത്തിന്റെ ആദ്യരൂപങ്ങള് കാണുക. |
'''ഹൈറോഗ്ളിഫിക്സ്'''. ഈജിപ്തില് വലത്തുനിന്ന് ഇടത്തോട്ടാണ് പഴയ എഴുത്ത്. | '''ഹൈറോഗ്ളിഫിക്സ്'''. ഈജിപ്തില് വലത്തുനിന്ന് ഇടത്തോട്ടാണ് പഴയ എഴുത്ത്. | ||
| - | + | [[Image:pno23 hiro1.png]] | |
| - | + | ||
| - | [[Image: | + | |
| - | 2312841 = 2(10)6 + 3(10)5 + 1(10)4 + 2(10)3 + 8 (10)2 + 4 (10) + 1. ഇതെഴുതുന്നത് ഇങ്ങനെയാണ്. | + | 2312841 = 2(10)<sup>6</sup> + 3(10)<sup>5</sup> + 1(10)<sup>4</sup> + 2(10)<sup>3</sup> + 8 (10)<sup>2</sup> + 4 (10) + 1. ഇതെഴുതുന്നത് ഇങ്ങനെയാണ്. |
[[Image:p23b.png]] | [[Image:p23b.png]] | ||
| വരി 24: | വരി 22: | ||
പിരമിഡുകളിലും മറ്റും ഇത്തരം ചിത്രലേഖനങ്ങള് കാണാം. | പിരമിഡുകളിലും മറ്റും ഇത്തരം ചിത്രലേഖനങ്ങള് കാണാം. | ||
| - | [[Image: | + | [[Image:pno23pattika1 a.png|right]] |
| - | + | ||
ബാബിലോണിന്റെ പരിസരങ്ങളില് കളിമണ് പലകകളില് എഴുതി ചൂളയ്ക്കുവച്ച് ഉറപ്പുവരുത്തി രേഖകളായി സൂക്ഷിച്ചിട്ടുള്ള ചരിത്രാവശിഷ്ടങ്ങളില് കാണുന്ന ക്യൂനിഫോം (cuniform) സമ്പ്രദായത്തില് 1, 10 എന്നിവയുടെ ചിഹ്നങ്ങള് യഥാക്രമം പട്ടിക എ-യില് ചേര്ത്തിരിക്കുന്നു. 60 വരെയുള്ള എണ്ണങ്ങള്ക്ക് ഈ രൂപങ്ങള് ഉപയോഗിച്ചിരുന്നു. | ബാബിലോണിന്റെ പരിസരങ്ങളില് കളിമണ് പലകകളില് എഴുതി ചൂളയ്ക്കുവച്ച് ഉറപ്പുവരുത്തി രേഖകളായി സൂക്ഷിച്ചിട്ടുള്ള ചരിത്രാവശിഷ്ടങ്ങളില് കാണുന്ന ക്യൂനിഫോം (cuniform) സമ്പ്രദായത്തില് 1, 10 എന്നിവയുടെ ചിഹ്നങ്ങള് യഥാക്രമം പട്ടിക എ-യില് ചേര്ത്തിരിക്കുന്നു. 60 വരെയുള്ള എണ്ണങ്ങള്ക്ക് ഈ രൂപങ്ങള് ഉപയോഗിച്ചിരുന്നു. | ||
ഉദാ. 23 = [[Image:p23d.png]] | ഉദാ. 23 = [[Image:p23d.png]] | ||
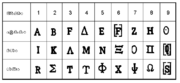
| - | ഗ്രീസില് രണ്ടു സമ്പ്രദായങ്ങളുണ്ടായിരുന്നു. ഒന്നാമതായി, 1 ഒമ്പതു പ്രാവശ്യം ആവര്ത്തിക്കപ്പെടുകയും 10-ന് ഒരു ഒറ്റയടയാളം ചേര്ക്കുകയുമാണ്; രണ്ടാമതായി, എളുപ്പമായ ഗ്രൂപ്പിംഗ് സമ്പ്രദായവും. ഇതിനു മുമ്പുതന്നെ ബാബിലോണിയക്കാരും ഈജിപ്തുകാരും ഫിനീഷ്യക്കാരും 1 ഒമ്പതുവരെ ആവര്ത്തിക്കുന്ന സമ്പ്രദായവും പ്രയോഗിച്ചിരുന്നു. 10, 100, 1000 എന്നിവയുടെ (ക്രീറ്റില് നിലവിലിരുന്ന) ചിഹ്നങ്ങള് ക്രമത്തില് പട്ടിക ബി-യില് ചേര്ത്തിരിക്കുന്നു. | + | ഗ്രീസില് രണ്ടു സമ്പ്രദായങ്ങളുണ്ടായിരുന്നു. ഒന്നാമതായി, 1 ഒമ്പതു പ്രാവശ്യം ആവര്ത്തിക്കപ്പെടുകയും 10-ന് ഒരു ഒറ്റയടയാളം ചേര്ക്കുകയുമാണ്; രണ്ടാമതായി, എളുപ്പമായ ഗ്രൂപ്പിംഗ് സമ്പ്രദായവും. ഇതിനു മുമ്പുതന്നെ ബാബിലോണിയക്കാരും ഈജിപ്തുകാരും ഫിനീഷ്യക്കാരും 1 ഒമ്പതുവരെ ആവര്ത്തിക്കുന്ന സമ്പ്രദായവും പ്രയോഗിച്ചിരുന്നു. 10, 100, 1000 എന്നിവയുടെ (ക്രീറ്റില് നിലവിലിരുന്ന) ചിഹ്നങ്ങള് ക്രമത്തില് പട്ടിക ബി-യില് ചേര്ത്തിരിക്കുന്നു.[[Image:pno23pattikaB.png|right]]വാക്കുകളുടെ ആദ്യക്ഷരങ്ങള് കൊണ്ട് സംഖ്യകള് ചുരുക്കമായി എഴുതുന്ന രീതിയില് നിന്നാണ് പിന്നീട് അക്ഷരസംഖ്യാ സമ്പ്രദായം ഉണ്ടായത്. ഇന്ത്യയിലെ കലി സംഖ്യ (പരല്പേര്) ഇതിനുദാഹരണമാണ്. 5, 10, 100, 1,000, 10,000 എന്നിവ ക്രമത്തില് π (അഥവാ Γ) Δ, H, X, M (അഥവാ MU ) ഉപയോഗിച്ചു. അക്കങ്ങള് 5 നോടു ചേര്ത്ത് കൂട്ടക്കങ്ങളെഴുതി: |
| - | + | ||
| - | [[Image: | + | |
| - | + | ||
| - | വാക്കുകളുടെ ആദ്യക്ഷരങ്ങള് കൊണ്ട് സംഖ്യകള് ചുരുക്കമായി എഴുതുന്ന രീതിയില് നിന്നാണ് പിന്നീട് അക്ഷരസംഖ്യാ സമ്പ്രദായം ഉണ്ടായത്. ഇന്ത്യയിലെ കലി സംഖ്യ (പരല്പേര്) ഇതിനുദാഹരണമാണ്. 5, 10, 100, 1,000, 10,000 എന്നിവ ക്രമത്തില് | + | |
| - | + | ||
| - | + | ||
| - | + | [[Image:pno23f1.png]]ഇത്തരത്തില്. 25436 = MM|XHHHHΔΔΔπ1.ബി.സി. മൂന്നും രണ്ടും ശ.-ങ്ങളില് ഈ സമ്പ്രദായം നിലനിന്നിരുന്നതായി ആറ്റിക് ശാസനങ്ങള് വെളിപ്പെടുത്തുന്നു. ഹെറോഡിയാനിക് അക്കങ്ങളെന്നാണ് ഇതിനു പേര്. | |
| - | [[Image: | + | '''റോമന് പദ്ധതി'''. റോമന് സമ്പ്രദായം ഏകദേശം 2,000 വര്ഷങ്ങളോളം എല്ലാ രംഗത്തും നിലനിന്നു. [[Image:pno23pattikaC.png|right]] |
| + | V,X,L,C എന്നീ നാല് അക്കങ്ങള് ഓര്മിച്ചാല് മറ്റെല്ലാം എളുപ്പം എഴുതാവുന്നതിനാലും III, VII എന്നിവ 3, 7 എന്നിവയെക്കാള് എളുപ്പം ഗ്രഹിക്കാവുന്നതായതിനാലും ഏറെക്കാലം ഈ സമ്പ്രദായം നിലനിന്നു. നിവര്ത്തിപ്പിടിച്ച കൈപ്പത്തിയുടെ ആകൃതിയിലുള്ള ചിഹ്നമാണ് V. ഇതുപോലെ രണ്ടെണ്ണമായാല് X എന്നായി; ഇതാണ് പത്ത്; [[Image:pno23romana.png]]പിന്നീട് L ആയി 50-ന്; ø (തീറ്റാ), പിന്നീട് C 100 നെയും സൂചിപ്പിച്ചു; ø (ഫൈ), പിന്നീട് I അഥവാ M 1,000 വും 10, 50, 100, 1000 എന്നിവയുടെ ചിഹ്നങ്ങള് ക്രമത്തില് പട്ടിക സി-യില് കാണാം. | ||
ബി.സി. 260-ല് റോമാക്കാര് കാര്തേജിയന്മാരുടെ മേല് നേടിയ വിജയത്തെ അനുസ്മരിച്ച് സ്ഥാപിക്കപ്പെട്ട സ്തംഭത്തിന്മേല് (Columna Rostrata) കാണുന്ന അക്കങ്ങളാണ് വലിയ സംഖ്യകളുടെ ഏറ്റവും പ്രാചീനമായ രേഖകള്. ഇതില് (((1))) എന്നിങ്ങനെ 23 പ്രാവശ്യം ആവര്ത്തിച്ചു കാണുന്നത് 23,00,000 ആണ്. | ബി.സി. 260-ല് റോമാക്കാര് കാര്തേജിയന്മാരുടെ മേല് നേടിയ വിജയത്തെ അനുസ്മരിച്ച് സ്ഥാപിക്കപ്പെട്ട സ്തംഭത്തിന്മേല് (Columna Rostrata) കാണുന്ന അക്കങ്ങളാണ് വലിയ സംഖ്യകളുടെ ഏറ്റവും പ്രാചീനമായ രേഖകള്. ഇതില് (((1))) എന്നിങ്ങനെ 23 പ്രാവശ്യം ആവര്ത്തിച്ചു കാണുന്നത് 23,00,000 ആണ്. | ||
| - | [[Image: | + | [[Image:hebronumbers.png|thumb| ഹീബ്രു അക്കസമ്പ്രദായം ]] |
| - | [[Image: | + | [[Image:chinesenumbers.png|thumb| ചൈനയിലെ അക്കസമ്പ്രദായം]] |
ഇതില്നിന്ന് (1) = 1,000, ((1)) = 10,000, (((1))) = 1,00,000 എന്ന് ഊഹിക്കാം. അച്ചടി സാധാരണമായതിനുശേഷവും ഈ സമ്പ്രദായം നിലനിന്നു. ചിഹ്നത്തിന്റെ മുകളില് ഒരു വരയിട്ട് 1,000 ത്തിന്റെ പെരുക്കത്തെ സൂചിപ്പിക്കുന്ന സമ്പ്രദായം മധ്യകാലത്തു പ്രചാരത്തിലിരുന്നു. ഈ രീതി റോമില് ഉണ്ടായിരുന്നില്ല. കുറച്ചെഴുതുന്ന സമ്പ്രദായം ഹീബ്രുവിലും ചില റോമന് അക്കങ്ങളിലുമുണ്ട്. IV, IX എന്നിവ ഉദാഹരണങ്ങളാണ്. ഗുണിച്ചെഴുതി ഗ്രൂപ്പു ചെയ്യുന്ന സമ്പ്രദായം ചൈനയിലുണ്ടായിരുന്നു. സ്ഥാനമനുസരിച്ചുള്ള എഴുത്താണ് ആധുനിക ചൈനയില് നിലവിലുള്ളത്. പൂജ്യത്തെ o എന്ന വൃത്തചിഹ്നംകൊണ്ടാണ് സൂചിപ്പിക്കുന്നത്. | ഇതില്നിന്ന് (1) = 1,000, ((1)) = 10,000, (((1))) = 1,00,000 എന്ന് ഊഹിക്കാം. അച്ചടി സാധാരണമായതിനുശേഷവും ഈ സമ്പ്രദായം നിലനിന്നു. ചിഹ്നത്തിന്റെ മുകളില് ഒരു വരയിട്ട് 1,000 ത്തിന്റെ പെരുക്കത്തെ സൂചിപ്പിക്കുന്ന സമ്പ്രദായം മധ്യകാലത്തു പ്രചാരത്തിലിരുന്നു. ഈ രീതി റോമില് ഉണ്ടായിരുന്നില്ല. കുറച്ചെഴുതുന്ന സമ്പ്രദായം ഹീബ്രുവിലും ചില റോമന് അക്കങ്ങളിലുമുണ്ട്. IV, IX എന്നിവ ഉദാഹരണങ്ങളാണ്. ഗുണിച്ചെഴുതി ഗ്രൂപ്പു ചെയ്യുന്ന സമ്പ്രദായം ചൈനയിലുണ്ടായിരുന്നു. സ്ഥാനമനുസരിച്ചുള്ള എഴുത്താണ് ആധുനിക ചൈനയില് നിലവിലുള്ളത്. പൂജ്യത്തെ o എന്ന വൃത്തചിഹ്നംകൊണ്ടാണ് സൂചിപ്പിക്കുന്നത്. | ||
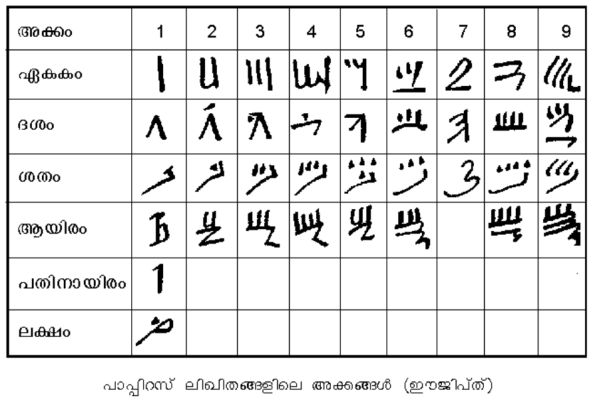
| - | സൈഫറിംഗ് (Ciphering) പദ്ധതി. പാപ്പിറസിനെ (pappyrus)ക്കുറിച്ച് പ്രതിപാദിക്കുന്ന ഈജിപ്ഷ്യന് ഗണിത രേഖകളില്നിന്ന് ഗ്രഹിക്കാവുന്നതാണ് ഹെറാറ്റിക് അക്കങ്ങള്. സൈഫറിംഗ് അക്കപദ്ധതിയിലെ ഏറ്റവും പഴക്കമുള്ളത് ഹെറാറ്റിക് അക്കങ്ങളാണ്: 1, 2, ..., 9; | + | '''സൈഫറിംഗ്''' (Ciphering) '''പദ്ധതി'''. പാപ്പിറസിനെ (pappyrus)ക്കുറിച്ച് പ്രതിപാദിക്കുന്ന ഈജിപ്ഷ്യന് ഗണിത രേഖകളില്നിന്ന് ഗ്രഹിക്കാവുന്നതാണ് ഹെറാറ്റിക് അക്കങ്ങള്. സൈഫറിംഗ് അക്കപദ്ധതിയിലെ ഏറ്റവും പഴക്കമുള്ളത് ഹെറാറ്റിക് അക്കങ്ങളാണ്: 1, 2, ..., 9; X , 2 X, ...., 9X; C, 2C, ...., 9 C; M, 2M ...., 9M. പിന്നീട് നിലനിന്നിരുന്ന ഡിമോടിക് അക്കങ്ങള് ഇതിന്റെ വകഭേദമാണ്. |
ബി.സി. 3-ാം ശ.-ത്തില് ഗ്രീസില് മറ്റൊരു രീതിയും നിലനിന്നിരുന്നു. ആദ്യക്ഷരങ്ങള് ഉപയോഗിച്ചുകൊണ്ടുള്ള സംഖ്യാസമ്പ്രദായത്തോട് ഇതിന് സാമ്യമുണ്ട്. ഇതും സൈഫറിംഗ് പദ്ധതിതന്നെ. അക്ഷരമാലയില് നിന്ന്, 1 മുതല് 9 വരെയുള്ള അക്കങ്ങള്ക്കും 10, 20, ...., 90; 100, 200, ...., 900, .... എന്നിവയ്ക്കും ക്രമത്തില് അക്ഷരങ്ങള് ഉപയോഗിക്കുന്നു. 24 അക്ഷരങ്ങള് | ബി.സി. 3-ാം ശ.-ത്തില് ഗ്രീസില് മറ്റൊരു രീതിയും നിലനിന്നിരുന്നു. ആദ്യക്ഷരങ്ങള് ഉപയോഗിച്ചുകൊണ്ടുള്ള സംഖ്യാസമ്പ്രദായത്തോട് ഇതിന് സാമ്യമുണ്ട്. ഇതും സൈഫറിംഗ് പദ്ധതിതന്നെ. അക്ഷരമാലയില് നിന്ന്, 1 മുതല് 9 വരെയുള്ള അക്കങ്ങള്ക്കും 10, 20, ...., 90; 100, 200, ...., 900, .... എന്നിവയ്ക്കും ക്രമത്തില് അക്ഷരങ്ങള് ഉപയോഗിക്കുന്നു. 24 അക്ഷരങ്ങള് | ||
| - | [[Image: | + | [[Image:pno24Pappiras.png]] |
| - | മാത്രമുള്ള ഗ്രീക് അക്ഷരമാല മതിയാകാതെ വന്നു. ഫിനീഷ്യന് ഭാഷയില്നിന്ന് | + | മാത്രമുള്ള ഗ്രീക് അക്ഷരമാല മതിയാകാതെ വന്നു. ഫിനീഷ്യന് ഭാഷയില്നിന്ന് F (വോ), യ (കോഫ്), S (സാമ്പി) എന്നിവയ്ക്കു സാമ്യമുള്ള അക്ഷരങ്ങള് അവര് സ്വീകരിച്ചു. |
| - | സ്ഥാനക്രമമനുസരിച്ചുള്ള സമ്പ്രദായമാണ് ഏറ്റവും ആധുനികം. എത്ര വലിയ സംഖ്യയായാലും എഴുതിക്കാണിക്കാന് ഏറ്റവും എളുപ്പമാര്ഗം ഇതാണ്. ഏതെങ്കിലുമൊരു അക്കം ആധാരമായെടുക്കാം. N = | + | സ്ഥാനക്രമമനുസരിച്ചുള്ള സമ്പ്രദായമാണ് ഏറ്റവും ആധുനികം. എത്ര വലിയ സംഖ്യയായാലും എഴുതിക്കാണിക്കാന് ഏറ്റവും എളുപ്പമാര്ഗം ഇതാണ്. ഏതെങ്കിലുമൊരു അക്കം ആധാരമായെടുക്കാം. N=b<sub>n</sub> a<sup>n</sup> + b<sub>n-1</sub> a<sup>n-1</sup> + .. + |
| + | b<sub>1</sub> a + b<sub>0</sub>.5623 =5M6C2X3എന്ന പഴയ സമ്പ്രദായം ക്ളേശകരമാണ്. Nന്റെ വിവരണവ്യഞ്ജകത്തില് ഏതെങ്കിലും പദം ഇല്ലെങ്കില് ആ സ്ഥാനം | ||
| - | [[Image: | + | [[Image:greekletters.png|thumb|ഗ്രീക്ക് അക്കങ്ങള്(ബി.സി.3ാംശ]] |
കുറിക്കാന് ഏതെങ്കിലുമൊരു ചിഹ്നം ആവശ്യമായി വന്നു. അല്ലെങ്കില് 356-ഉം 3056-ഉം ഒരുപോലെയിരിക്കും. ബി.സി. 3000-ത്തിനും 2000-ത്തിനുമിടയ്ക്ക് 60 ആധാരമാക്കി ഒരു സ്ഥാനക്രമസമ്പ്രദായമുണ്ടായി. 1 മുതല് 59 വരെയുള്ള അക്കങ്ങള്ക്കു പേരുകള് കണ്ടെത്തുക പ്രയാസമായി ഈ സമ്പ്രദായത്തില് | കുറിക്കാന് ഏതെങ്കിലുമൊരു ചിഹ്നം ആവശ്യമായി വന്നു. അല്ലെങ്കില് 356-ഉം 3056-ഉം ഒരുപോലെയിരിക്കും. ബി.സി. 3000-ത്തിനും 2000-ത്തിനുമിടയ്ക്ക് 60 ആധാരമാക്കി ഒരു സ്ഥാനക്രമസമ്പ്രദായമുണ്ടായി. 1 മുതല് 59 വരെയുള്ള അക്കങ്ങള്ക്കു പേരുകള് കണ്ടെത്തുക പ്രയാസമായി ഈ സമ്പ്രദായത്തില് | ||
| - | 2,56,058 = (60)3 + 11 (60)2 + 47 (60) + 38 = [[Image:p23k.png]] | + | 2,56,058 = (60)<sup>3</sup> + 11 (60)<sup>2</sup> + 47 (60) + 38 = [[Image:p23k.png]] |
| - | |||
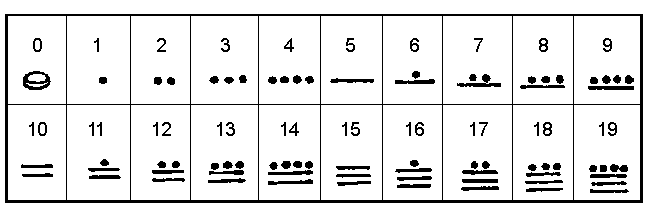
മയന് സമ്പ്രദായം. കാലനിര്ണയം ചെയ്യാന് കഴിയാത്ത ഒരു പ്രാചീന കാലഘട്ടത്തില് തന്നെ സ്ഥാനക്രമമനുസരിച്ചുള്ള ഒരു അക്കസമ്പ്രദായം അമേരിക്കയിലെ മയന്കാര്ക്കുണ്ടായിരുന്നതായി കാണുന്നു. 20 ആധാരമാക്കിക്കൊണ്ടുള്ള ഈ സമ്പ്രദായത്തില് 1 മുതല് 19 വരെയുള്ളവയ്ക്ക് 5-ന്റെ ചിഹ്നത്തോടു ഗ്രൂപ്പു ചെയ്തുകൊണ്ടുള്ള ചിഹ്നങ്ങളാണ് ഉപയോഗിച്ചിരുന്നത്. | മയന് സമ്പ്രദായം. കാലനിര്ണയം ചെയ്യാന് കഴിയാത്ത ഒരു പ്രാചീന കാലഘട്ടത്തില് തന്നെ സ്ഥാനക്രമമനുസരിച്ചുള്ള ഒരു അക്കസമ്പ്രദായം അമേരിക്കയിലെ മയന്കാര്ക്കുണ്ടായിരുന്നതായി കാണുന്നു. 20 ആധാരമാക്കിക്കൊണ്ടുള്ള ഈ സമ്പ്രദായത്തില് 1 മുതല് 19 വരെയുള്ളവയ്ക്ക് 5-ന്റെ ചിഹ്നത്തോടു ഗ്രൂപ്പു ചെയ്തുകൊണ്ടുള്ള ചിഹ്നങ്ങളാണ് ഉപയോഗിച്ചിരുന്നത്. | ||
| - | [[Image: | + | [[Image:Pno24(4).png|thumbs|centre|മയന് അക്കസമ്പ്രദായം]] |
| - | ഇന്ത്യന് സമ്പ്രദായം. വളരെ പ്രാചീനകാലം മുതല് ഇന്ത്യയില് സംഖ്യകളുടെ ആധാരമായി 'പത്ത്' സ്വീകരിച്ചിരുന്നു. പത്ത് ഒഴിച്ച് മറ്റൊരു ആധാരം (Base) വ്യാപകമായി ഉപയോഗിച്ചിരുന്നതിന്റെ പരാമര്ശം സംസ്കൃത സാഹിത്യം ആകെ പരിശോധിച്ചാലും കാണുകയില്ല. വളരെ ഉയര്ന്ന സംഖ്യകള്ക്ക് പേരുകളും ഇന്ത്യയില് നിലവിലുണ്ടായിരുന്നു. പതിനായിര ( | + | '''ഇന്ത്യന് സമ്പ്രദായം'''. വളരെ പ്രാചീനകാലം മുതല് ഇന്ത്യയില് സംഖ്യകളുടെ ആധാരമായി 'പത്ത്' സ്വീകരിച്ചിരുന്നു. പത്ത് ഒഴിച്ച് മറ്റൊരു ആധാരം (Base) വ്യാപകമായി ഉപയോഗിച്ചിരുന്നതിന്റെ പരാമര്ശം സംസ്കൃത സാഹിത്യം ആകെ പരിശോധിച്ചാലും കാണുകയില്ല. വളരെ ഉയര്ന്ന സംഖ്യകള്ക്ക് പേരുകളും ഇന്ത്യയില് നിലവിലുണ്ടായിരുന്നു. പതിനായിര (10<sup>4</sup>) ത്തില് കവിഞ്ഞ സംഖ്യകളുടെ പേരുകള് ഗ്രീക്കുകാര്ക്കുണ്ടായിരുന്നില്ല. റോമാക്കാര്ക്ക് ആയിര(10<sup>3</sup.>)ത്തില് കവിഞ്ഞ ഒരു സംഖ്യക്കും പേരുണ്ടായിരുന്നില്ല. ഇന്ത്യയിലാകട്ടെ പതിനെട്ടു സ്ഥാനങ്ങളില് കവിഞ്ഞ സംഖ്യകള്ക്കു വരെ പ്രത്യേകം പേരുകള് ഉണ്ടായിരുന്നു. |
യജൂര്വേദസംഹിതയില് (xvii-2) താഴെക്കാണുന്ന പേരുകള് അക്കങ്ങള്ക്കുപയോഗിച്ചിരുന്നു: ഏകം (1), ദശം (10), ശതം (100), സഹസ്രം (1,000), അയുതം (10,000), നിയുതം (1,00,000), പ്രയുതം (10,00,000), അര്ബുദം (1,00,00,000), നയാര്ബുദം (10,00,00,000), സമുദ്രം (1,00,00,00,000), മധ്യം (10,00,00,00,000), അന്തം (1,00,00,00,00,000), പരാര്ധം (10,00,00,00,00,000). തൈത്തിരീയസംഹിതയിലും (iv. 40. 11.4;vii. 2. 20. 1) ഇതേ പേരുകള് ഉപയോഗിച്ചിട്ടുണ്ട്. ചില്ലറ വ്യതിയാനങ്ങളോടെ ഈ പട്ടിക മൈത്രായനിയിലും (ii,8,14.) കാഠകസംഹിതയിലും(xvii-10) ഉപയോഗിച്ചിരുന്നതായി കാണാം. ബി.സി. 5-ാം ശ.-ത്തിലെ ബൌദ്ധകൃതിയായ ലളിതവിസ്താരത്തില് രാജേന്ദ്രലാല് മിത്ര, കോടിയില് കവിഞ്ഞ സംഖ്യകളുടെ പേരുകള് പരാമര്ശിക്കുന്നുണ്ട്. | യജൂര്വേദസംഹിതയില് (xvii-2) താഴെക്കാണുന്ന പേരുകള് അക്കങ്ങള്ക്കുപയോഗിച്ചിരുന്നു: ഏകം (1), ദശം (10), ശതം (100), സഹസ്രം (1,000), അയുതം (10,000), നിയുതം (1,00,000), പ്രയുതം (10,00,000), അര്ബുദം (1,00,00,000), നയാര്ബുദം (10,00,00,000), സമുദ്രം (1,00,00,00,000), മധ്യം (10,00,00,00,000), അന്തം (1,00,00,00,00,000), പരാര്ധം (10,00,00,00,00,000). തൈത്തിരീയസംഹിതയിലും (iv. 40. 11.4;vii. 2. 20. 1) ഇതേ പേരുകള് ഉപയോഗിച്ചിട്ടുണ്ട്. ചില്ലറ വ്യതിയാനങ്ങളോടെ ഈ പട്ടിക മൈത്രായനിയിലും (ii,8,14.) കാഠകസംഹിതയിലും(xvii-10) ഉപയോഗിച്ചിരുന്നതായി കാണാം. ബി.സി. 5-ാം ശ.-ത്തിലെ ബൌദ്ധകൃതിയായ ലളിതവിസ്താരത്തില് രാജേന്ദ്രലാല് മിത്ര, കോടിയില് കവിഞ്ഞ സംഖ്യകളുടെ പേരുകള് പരാമര്ശിക്കുന്നുണ്ട്. | ||
| - | ജൈനന്മാരുടെ | + | ജൈനന്മാരുടെ മൗലികകൃതിയായ അനുയോഗദ്വാരസൂത്രത്തില് (ബി.സി. 100) ലോകജനസംഖ്യ തിട്ടപ്പെടുത്തുമ്പോള് 194 ദശസ്ഥാനങ്ങള് ഉള്ള ഒരു സംഖ്യയാണതെന്നു പറയുന്നു. ആര്യഭടന് 1 (499), ശ്രീധരാചാര്യന് (750), മഹാവീരന് (850), ഭാസ്കരാചാര്യന് II (1150), നാരായണാചാര്യന് (1356) എന്നീ ഭാരതീയ ഗണിതാചാര്യന്മാരെല്ലാം ദശസ്ഥാനങ്ങള് ഉപയോഗിച്ചിരുന്നു. |
ഒന്നുമുതല് പത്തൊമ്പതുവരെ സ്ഥാനമുള്ള സംഖ്യകള്ക്ക് ഭാസ്കരാചാര്യന് ലീലാവതിയില് നാമനിര്ദേശം ചെയ്തിട്ടുണ്ട്. | ഒന്നുമുതല് പത്തൊമ്പതുവരെ സ്ഥാനമുള്ള സംഖ്യകള്ക്ക് ഭാസ്കരാചാര്യന് ലീലാവതിയില് നാമനിര്ദേശം ചെയ്തിട്ടുണ്ട്. | ||
'ഏക, ദശ, ശത, സഹസ്റാ,- | 'ഏക, ദശ, ശത, സഹസ്റാ,- | ||
| + | |||
യുത, ലക്ഷ, പ്രയുത, കോടയഃ ക്രമശഃ | യുത, ലക്ഷ, പ്രയുത, കോടയഃ ക്രമശഃ | ||
| + | |||
അര്ബുദ, മബ്ജം, ഖര്വ,- | അര്ബുദ, മബ്ജം, ഖര്വ,- | ||
| + | |||
നിഖര്വ, മഹാപദ്മ, ശങ്കവസ്തസ്മാത് | നിഖര്വ, മഹാപദ്മ, ശങ്കവസ്തസ്മാത് | ||
| + | |||
ജലധി, ശ്ചാന്ത്യം, മധ്യം, | ജലധി, ശ്ചാന്ത്യം, മധ്യം, | ||
| + | |||
പരാര്ധ, മിതി ദശഗുണോത്തരാഃ, സംജ്ഞാഃ | പരാര്ധ, മിതി ദശഗുണോത്തരാഃ, സംജ്ഞാഃ | ||
| + | |||
സംഖ്യായാഃ സ്ഥാനാനാം | സംഖ്യായാഃ സ്ഥാനാനാം | ||
| + | |||
വ്യവഹാരാര്ഥം കൃതാഃ പൂര്വൈഃ' | വ്യവഹാരാര്ഥം കൃതാഃ പൂര്വൈഃ' | ||
ഭാരതീയ ഗണിതശാസ്ത്രപ്രകാരം ഇങ്ങനെ പേരു നല്കപ്പെട്ടിട്ടുള്ള സംഖ്യകളെല്ലാം തന്നെ പത്തിന്റെ (10) അനുക്രമമായ ഘാത(ഗുണിത)ങ്ങളാണെന്ന് പ്രത്യേകം ഓര്മിക്കേണ്ടതുണ്ട്. മേലെഴുതിയ പേരുകള് സൂചിപ്പിക്കുന്ന സംഖ്യകളുടെ പട്ടിക താഴെ കൊടുക്കുന്നു: | ഭാരതീയ ഗണിതശാസ്ത്രപ്രകാരം ഇങ്ങനെ പേരു നല്കപ്പെട്ടിട്ടുള്ള സംഖ്യകളെല്ലാം തന്നെ പത്തിന്റെ (10) അനുക്രമമായ ഘാത(ഗുണിത)ങ്ങളാണെന്ന് പ്രത്യേകം ഓര്മിക്കേണ്ടതുണ്ട്. മേലെഴുതിയ പേരുകള് സൂചിപ്പിക്കുന്ന സംഖ്യകളുടെ പട്ടിക താഴെ കൊടുക്കുന്നു: | ||
| - | + | 1 ഏകം | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | 10 ദശം | |
| - | + | 100 ശതം | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | 1,000 സഹസ്രം | |
| - | + | ||
| - | + | ||
| - | + | 10,000 അയുതം | |
| - | + | 1,00,000 ലക്ഷം | |
| - | + | 10,00,000 പ്രയുതം | |
| + | |||
| + | 1,00,00,000 കോടി | ||
| + | |||
| + | 10,00,00,000 അര്ബുദം | ||
| + | |||
| + | 1,00,00,00,000 അബ്ജം | ||
| + | |||
| + | 10,00,00,00,000 ഖര്വം | ||
| + | |||
| + | 1,00,00,00,00,000 നിഖര്വം | ||
| + | |||
| + | 10,00,00,00,00,000 മഹാപദ്മം | ||
| + | |||
| + | 1,00,00,00,00,00,000 ശങ്കു | ||
| + | |||
| + | 10,00,00,00,00,00,000 ജലധി (സമുദ്രം) | ||
| + | |||
| + | 1,00,00,00,00,00,00,000 അന്ത്യം | ||
| + | |||
| + | 10,00,00,00,00,00,00,000 മധ്യം | ||
| + | |||
| + | 1,00,00,00,00,00,00,00,000 പരാര്ധം | ||
| + | |||
| + | 10,00,00,00,00,00,00,00,000 ദശപരാര്ധം | ||
| - | + | സങ്കല്പാതീതമെന്ന് പറയാവുന്നതും സാമാന്യരീതിയില് എണ്ണിത്തീര്ക്കാന് ദുഷ്കരമായതും ആയ മഹാസംഖ്യകള്ക്ക് മലയാളത്തില് 'വെള്ളം' എന്നു പറഞ്ഞുവരുന്ന പതിവുണ്ടായിരുന്നു. ഭാസ്കരാചാര്യന്റെ ലീലാവതിയിലെ 'ജലധി'യില് (സമുദ്രം) നിന്നാകാം ഈ വിവര്ത്തിത സംജ്ഞ മലയാളത്തിന് കിട്ടിയത്. 'വെള്ളം പട' എന്നത് ഒരു വലിയ സംഖ്യക്കു പകരം മലയാളത്തില് ഇപ്പോഴും പറഞ്ഞുവരുന്ന പേരാണ്. പരമ്പരാഗതമായ ഈ വ്യവഹാരരീതി താഴെ കൊടുക്കുന്നു: | |
| - | [[Image: | + | [[Image:pno25nooru.png]] |
| - | + | പാശ്ചാത്യ ഗണനപദ്ധതി അനുസരിച്ച് പ്രത്യേക സംജ്ഞ നല്കപ്പെട്ടിട്ടുള്ള ഏറ്റവും വലിയ സംഖ്യ 'ബില്യണ്' (billion) ആണ്. ഇതിലടങ്ങിയിരിക്കുന്ന സ്ഥാന(അക്ക)ങ്ങളെ സംബന്ധിച്ച് യു.എസിലും ഫ്രാന്സിലും ഒരു രീതിയും (1,00,00,00,000) ബ്രിട്ടനിലും ജര്മനിയിലും മറ്റൊരു രീതിയും (10,00,00,00,00,000) ആണ് പ്രചാരത്തിലിരിക്കുന്നത്. ഇപ്പോള് യു.എസ്. രീതി ഏതാണ്ട് സര്വസമ്മതമായി അംഗീകരിക്കപ്പെട്ടിരിക്കുന്നു. അതായത് 1 ബില്യണ് = 10<sup>9</sup> ആയിരം ബില്യണ് സമം ഒരു ട്രില്യണ് (Trillion). ഒരു ട്രില്യണ് = 10<sup>12</sup>. | |
| - | + | '''പ്രാചീന അക്കങ്ങള്'''. മോഹഞ്ജൊദാരോയില് (ബി.സി. 5000) നിന്നു കണ്ടെടുത്ത പുരാരേഖകള് മുഴുവന് മനസിലാക്കാന് കഴിഞ്ഞിട്ടില്ല. എങ്കിലും കുത്തനെ ചെറുവരകള് നിരത്തിയോ ഒന്നിനു താഴെ മറ്റൊന്ന് എന്ന രൂപത്തിലോ അക്കങ്ങള് എഴുതിയിരുന്നു. | |
| - | + | മോഹഞ്ജൊദാരോ ലിഖിതങ്ങള്ക്കും അശോകലിഖിതങ്ങള്ക്കും ഇടയില് 2700 വര്ഷത്തോളം അക്കങ്ങള് എങ്ങനെ ഉപയോഗിച്ചിരുന്നുവെന്നതിനെക്കുറിച്ച് അറിവൊന്നും ലഭ്യമല്ല. ഋഗ്വേദത്തില് എട്ടിനെക്കുറിച്ചും യജൂര്വേദത്തില് 10<sup>12</sup> നോളം വലിയ സംഖ്യകളെക്കുറിച്ചുമുള്ള പരാമര്ശങ്ങള് വച്ചുനോക്കുമ്പോള് വളരെ വികാസം സിദ്ധിച്ച അക്കസമ്പ്രദായം ഇന്ത്യയില് നിലവിലിരുന്നുവെന്ന് ഊഹിക്കാന് കഴിയും. അശോകലിഖിതങ്ങളില് നിന്നും ഇന്ത്യയിലെ ഈ പ്രാചീനവികാസം ഗ്രഹിക്കാം. ആ ലിഖിതങ്ങള് ബ്രാഹ്മി, ഖരോഷ്ടി എന്നീ രണ്ടുതരം ലിപികളിലാണ് എഴുതിക്കാണുന്നത്. | |
| - | + | (i) '''ബ്രാഹ്മി അക്കങ്ങള്'''. ഇന്ത്യയില് എല്ലായിടത്തും പ്രചാരത്തിലിരുന്ന ഒരുതരം ലിപിയാണ് ബ്രാഹ്മി. ഇത് ഇന്ത്യയുടെ ദേശീയ ലിപിയായിരുന്നു. ബി.സി. 1000-ത്തിനു മുമ്പുതന്നെ ഈ ലിപി പരിഷ്കരിച്ച നിലയിലെത്തിയിരുന്നു. ബ്രാഹ്മി അക്കങ്ങള് ഇന്ത്യയില് കണ്ടുപിടിച്ചവയാണ്. ഈ സമ്പ്രദായവും വിദേശീയമാണെന്നുവരുത്താന് ചില ശ്രമങ്ങള് നടന്നിട്ടുണ്ട്. പക്ഷേ പ്രസിദ്ധ ചരിത്രകാരനായ ലാങ്ഡണിന്റെ (Langdon's Mohenjodaro and the Indus Vally Civilization,Ch,xxiii) അഭിപ്രായത്തില് ബ്രാഹ്മി അക്കങ്ങള് ഇന്ത്യയില് തന്നെയാണ് കണ്ടുപിടിക്കപ്പെട്ടത്. ബ്രാഹ്മി അക്കങ്ങള് അശോക ലിഖിതങ്ങളില് (ബി.സി. 300) നിന്നാണ് മനസിലാക്കുന്നത്. ഉദാ. | |
| - | + | [[Image:p.23 lepi-highgroglificks1 (7).jpg|thumb|centre]] | |
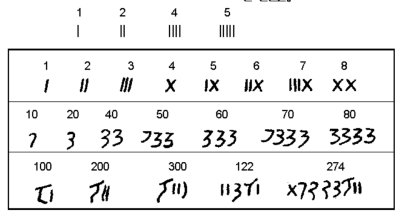
| - | + | മധ്യേന്ത്യയിലെ നാനാഘട്ട് കുന്നിന് മുകളിലുള്ള (പൂണൈയില് നിന്നു 120 കി.മീ. ദൂരെ) ഒരു ഗുഹയില് അക്കങ്ങള് കൊത്തിയ ലിഖിതങ്ങള് കണ്ടെത്തിയിട്ടുണ്ട്. ചില അക്കങ്ങള് താഴെ ചേര്ക്കുന്നു. (Journal of Bombay Branch of the Royal Aslatic Society , 1876, Vol,XII.P.404) | |
| - | + | ||
| - | [[Image: | + | [[Image:pno25Ad.png|thumb|right]] |
| - | + | എ.ഡി. ഒന്നോ രണ്ടോ ശ.-ത്തിലേതായി മഹാരാഷ്ട്രയിലെ നാസിക് ജില്ലയിലെ ഗുഹകളില് കണ്ടെത്തിയ ലിഖിതങ്ങളിലും അക്കങ്ങള് രേഖപ്പെടുത്തിയിരിക്കുന്നതു കാണാം. (The inscription in the caves at nasik,EI Vol VII,P.47-74). | |
| - | ( | + | [[Image:Pno25(3).png|thumb|right]] |
| - | + | പൂജ്യത്തിന്റെ കണ്ടുപിടിത്തത്തോടെ സ്ഥാനക്രമം അനുസരിക്കുന്ന അക്കസമ്പ്രദായവും പൂജ്യവും ഇന്ത്യയിലെന്നപോലെ മറ്റു രാജ്യങ്ങളിലും സ്വീകരിച്ചുകാണുന്നു. പൂജ്യത്തിന്റെയും സ്ഥാനക്രമസമ്പ്രദായത്തിന്റെയും കണ്ടുപിടിത്തം ഇന്ത്യയിലാണെന്നതിന് ഏറ്റവും വലിയ തെളിവും ഇതുതന്നെ. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | -, --, =,, എന്നിങ്ങനെ ഒന്ന്, രണ്ട്, മൂന്ന് എന്നിവ എഴുതുന്നതുകൊണ്ടുതന്നെ ബ്രാഹ്മി സമ്പ്രദായങ്ങളില് നിന്നും ഇതു വ്യത്യസ്തമാണ്. ഖരോഷ്ടിയിലും സെമിറ്റിക്കിലും I, II, III എന്നിങ്ങനെയാണ് എഴുതുന്നത്. 1, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, ........., 1000, 2000, ........ എന്നിവയ്ക്കെല്ലാം വ്യത്യസ്തമായ പ്രതീകങ്ങള് ബ്രാഹ്മി അക്കസമ്പ്രദായത്തിലുണ്ട്. എന്നാല് പഴയ ഖരോഷ്ടി അക്കസമ്പ്രദായത്തിലും ആദ്യകാല സെമിറ്റിക് രേഖകളിലും ഹൈറോഗ്ളിഫിക്സ് - ഫിനീഷ്യന് സമ്പ്രദായങ്ങളിലും 1, 10, 20, 100 എന്നിവയ്ക്കു മാത്രമേ പ്രതീകങ്ങളുള്ളു. ചിത്രമെഴുത്തില് നിന്നാണ് ഇന്ത്യയിലെ ബ്രാഹ്മി അക്കസമ്പ്രദായം രൂപപ്പെട്ടത് എന്നാണ് പല (Cunningham) ഇംഗ്ളീഷു ചരിത്രകാരന്മാരുടെയും അഭിപ്രായം. | |
| - | + | ||
| - | + | ||
| - | + | (ii) '''ഖരോഷ്ടി അക്കങ്ങള്'''. വലത്തുനിന്ന് ഇടത്തോട്ട് എഴുതുന്ന ഒരു ലിപി സമ്പ്രദായമാണ് ഖരോഷ്ടി. കിഴക്കന് അഫ്ഗാനിസ്താനിലും വടക്കെ പഞ്ചാബിലും (ഗാന്ധാരം) പ്രധാനമായി കണ്ടെത്തിയ ലിഖിതങ്ങള് ഖരോഷ്ടി ലിപിയിലുള്ളതാണ്. ബി.സി. നാലും മൂന്നും ശ.-ങ്ങളിലാണ് ഇതു പ്രചാരത്തിലിരുന്നത്. അശോകന്റെ ലിഖിതങ്ങളില്നിന്നു കണ്ടെത്തിയ ഖരോഷ്ടി ലിപിയില് നാല് അക്കങ്ങളേ ഉള്ളൂ: | |
| - | + | ||
| + | [[Image:pno26Haro.png]] | ||
| - | + | ശാകന്മാരുടെയും പാര്ത്തിയന്മാരുടെയും കുശാനന്മാരുടെയും ലിഖിതങ്ങളില്നിന്നും എ.ഡി. ഒന്നും രണ്ടും ശ.-ങ്ങളിലെ കുറേക്കൂടി പരിഷ്കരിച്ച ഖരോഷ്ടി അക്കങ്ങള് കണ്ടെത്തിയിട്ടുണ്ട്. | |
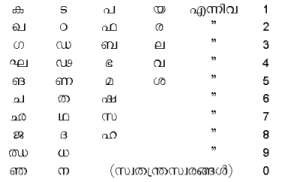
| - | + | (iii) '''കടപയാദി സമ്പ്രദായം'''. അക്ഷരങ്ങള് അക്കങ്ങളായി ഉപയോഗിക്കുന്ന രീതിയും ഇന്ത്യയില് ഉണ്ടായിരുന്നു. സംസ്കൃത ഭാഷയിലെ വ്യഞ്ജനങ്ങളും (ഒന്നു മുതല് ഒമ്പതുവരെയുള്ള അക്കങ്ങള്ക്ക്) പൂജ്യവും ഉപയോഗിക്കുന്ന അക്ഷരസമ്പ്രദായമാണ് ഇത്. അക്കങ്ങള് രേഖപ്പെടുത്തുന്നതോടൊപ്പം അര്ഥം സ്ഫുരിക്കുന്ന വിധത്തില് വ്യഞ്ജനങ്ങള് ചേര്ത്ത് പ്രയോഗിച്ച് കാവ്യാത്മകമായ രീതിയില് അവ സംവിധാനം ചെയ്യാന് പല എഴുത്തുകാര്ക്കും കഴിഞ്ഞിരുന്നു. ആര്യഭടന് I (എ.ഡി. 499) ഈ കലയില് അദ്വിതീയനായിരുന്നു. ഈ സമ്പ്രദായമനുസരിച്ചുള്ള പട്ടിക താഴെ കാണാം. | |
| + | [[Image:pno.26 swaram.png]] | ||
| - | |||
| - | + | [[Image:pno.26Swaram2.png]] | |
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
ഈ പട്ടികയില് (ആദ്യത്തെ വരി) ഒന്നിനെ പ്രതിനിധാനം ചെയ്യുന്നത് കടപയ ആയതിനാല് കടപയാദി എന്ന് ഈ സമ്പ്രദായത്തിന് പേരുണ്ടായി. | ഈ പട്ടികയില് (ആദ്യത്തെ വരി) ഒന്നിനെ പ്രതിനിധാനം ചെയ്യുന്നത് കടപയ ആയതിനാല് കടപയാദി എന്ന് ഈ സമ്പ്രദായത്തിന് പേരുണ്ടായി. | ||
| - | എ.ഡി. 6-ാം ശ.-ത്തിലാണ് ഈ സമ്പ്രദായം ഉണ്ടായത്. ഇത് കാണുന്ന ആദ്യത്തെ രേഖ, ഭാസ്കരാചാര്യന് | + | എ.ഡി. 6-ാം ശ.-ത്തിലാണ് ഈ സമ്പ്രദായം ഉണ്ടായത്. ഇത് കാണുന്ന ആദ്യത്തെ രേഖ, ഭാസ്കരാചാര്യന് I-ന്റെ (522) ലഘുഭാസ്കരീയം എന്ന ഗ്രന്ഥമാണ്. ആര്യഭടന് II (950) ഈ സമ്പ്രദായം പരിഷ്കരിച്ച് ഉപയോഗിച്ചിരുന്നു. ആദ്യത്തെ രീതിയില് സ്വരങ്ങള് സ്വതന്ത്രമായി നില്ക്കുമ്പോള് പൂജ്യത്തെ പ്രതിനിധാനം ചെയ്യുന്നില്ല. ഇതില് സ്വരങ്ങള്ക്ക് പ്രത്യേകിച്ച് അക്കങ്ങളുമായി ബന്ധമില്ല. മുമ്പുണ്ടായിരുന്ന സമ്പ്രദായത്തില് നിന്നും ഇതിന്റെ വ്യത്യാസം, കൂട്ടക്ഷരങ്ങളില് ഉള്പ്പെടുന്ന വ്യഞ്ജനങ്ങള് സ്ഥാനഭേദമനുസിച്ച് പ്രത്യേകം അക്കങ്ങളെ സൂചിപ്പിക്കുന്നു എന്നതാണ്. ഇടത്തുനിന്നു വലത്തോട്ട് എന്ന എഴുത്തുരീതിയാണിതില്. "ധജഹേ കുനഹേത് സഭാ'' എന്നത് ആദ്യസമ്പ്രദായത്തില് 47801884-ഉം രണ്ടാമത്തേതില് 48810874-ഉം ആണ് സൂചിപ്പിക്കുന്നത്. |
| - | പാലി അക്ഷരമാലയില് ശ, ഷ എന്നിവയില്ലാത്തതിനാല് | + | പാലി അക്ഷരമാലയില് ശ, ഷ എന്നിവയില്ലാത്തതിനാല് സ = 5, ഹ = 6, ഞ (?) = 7 തന്നെയാണ്. ബര്മയിലെ (മ്യാന്മര്) പാലി ഹസ്തലിഖിതങ്ങളില് പരിഷ്കരിച്ച ഈ കടപയാദി സമ്പ്രദായം ഉപയോഗിച്ചിരുന്നു. |
| - | + | ||
| - | സ = 5, ഹ = 6, ഞ (?) = 7 തന്നെയാണ്. ബര്മയിലെ (മ്യാന്മര്) പാലി ഹസ്തലിഖിതങ്ങളില് പരിഷ്കരിച്ച ഈ കടപയാദി സമ്പ്രദായം ഉപയോഗിച്ചിരുന്നു. | + | |
നാലാമത്തെ ഭേദഗതിയാണ് 'കേരളസമ്പ്രദായ'മെന്നു പ്രസിദ്ധമായത്. ഇതും ആദ്യത്തെ സമ്പ്രദായം തന്നെയാണ്. ഇതില് വലത്ത്-ഇടത്ത് എന്ന എഴുത്തുക്രമം മാറ്റി ഇടത്ത്-വലത്ത് എന്ന ക്രമം സ്വീകരിച്ചിരിക്കുന്നു. | നാലാമത്തെ ഭേദഗതിയാണ് 'കേരളസമ്പ്രദായ'മെന്നു പ്രസിദ്ധമായത്. ഇതും ആദ്യത്തെ സമ്പ്രദായം തന്നെയാണ്. ഇതില് വലത്ത്-ഇടത്ത് എന്ന എഴുത്തുക്രമം മാറ്റി ഇടത്ത്-വലത്ത് എന്ന ക്രമം സ്വീകരിച്ചിരിക്കുന്നു. | ||
| വരി 209: | വരി 176: | ||
കേരളം, ആന്ധ്ര, സിലോണ്, ബര്മ, സയാം (തായ്ലന്ഡ്), ശ്രീലങ്ക എന്നിവിടങ്ങളില് പ്രയോഗത്തിലിരുന്ന മറ്റുചില അക്ഷര സമ്പ്രദായങ്ങളുമുണ്ട്. സംസ്കൃതഭാഷയിലെ 16 സ്വരങ്ങളും 34 വ്യഞ്ജനങ്ങളും പ്രയോജനപ്പെടുത്തുന്ന രീതിയാണ് അതില്. വ്യഞ്ജനങ്ങള് ക്രമത്തില് 1 മുതല് 34 സംഖ്യകളെയും അവ തന്നെ 'ആ' കാരാന്ത്യമായി പ്രയോഗിച്ചാല് 35 മുതല് 68 വരെയും അങ്ങനെ തുടര്ന്നും പ്രയോഗിക്കാറുണ്ട്. ക, കാ, ..... എന്നു തുടങ്ങിയ 16 അക്ഷരങ്ങള് 1 മുതല് 16 സംഖ്യകളെയും ഖ, ഖാ, ...... എന്നീ പതിനാറെണ്ണം, പതിനേഴു മുതല് മുപ്പത്തിനാലുവരെയും അങ്ങനെ തുടര്ന്നുള്ളവയും പ്രയോഗിച്ചിരുന്ന മറ്റൊരു അക്ഷരസമ്പ്രദായവും ഉണ്ടായിരുന്നു. ഇത് ശ്രീലങ്കയിലെ പാലി ഹസ്തലിഖിതങ്ങളിലാണ് കണ്ടെത്തിയിട്ടുള്ളത്. പന്ത്രണ്ട് സ്വരങ്ങളും 34 വ്യഞ്ജനങ്ങളും ഉപയോഗിച്ചുകൊണ്ടുള്ള മറ്റൊരു സമ്പ്രദായവുമുണ്ട്, പാലി കയ്യെഴുത്തു പ്രതികളില്. ഇതില് ക, കാ, .... എന്നിങ്ങനെ 13 മുതല് 26 വരെയും തുടര്ന്നും കാണാം. എ.ഡി. 3-ാം ശ.-ത്തിനു മുമ്പുവരെയെങ്കിലും ഈ അക്ഷരസമ്പ്രദായം വടക്കെ ഇന്ത്യയില് ഉപയോഗിച്ചു കണ്ടിട്ടില്ല. | കേരളം, ആന്ധ്ര, സിലോണ്, ബര്മ, സയാം (തായ്ലന്ഡ്), ശ്രീലങ്ക എന്നിവിടങ്ങളില് പ്രയോഗത്തിലിരുന്ന മറ്റുചില അക്ഷര സമ്പ്രദായങ്ങളുമുണ്ട്. സംസ്കൃതഭാഷയിലെ 16 സ്വരങ്ങളും 34 വ്യഞ്ജനങ്ങളും പ്രയോജനപ്പെടുത്തുന്ന രീതിയാണ് അതില്. വ്യഞ്ജനങ്ങള് ക്രമത്തില് 1 മുതല് 34 സംഖ്യകളെയും അവ തന്നെ 'ആ' കാരാന്ത്യമായി പ്രയോഗിച്ചാല് 35 മുതല് 68 വരെയും അങ്ങനെ തുടര്ന്നും പ്രയോഗിക്കാറുണ്ട്. ക, കാ, ..... എന്നു തുടങ്ങിയ 16 അക്ഷരങ്ങള് 1 മുതല് 16 സംഖ്യകളെയും ഖ, ഖാ, ...... എന്നീ പതിനാറെണ്ണം, പതിനേഴു മുതല് മുപ്പത്തിനാലുവരെയും അങ്ങനെ തുടര്ന്നുള്ളവയും പ്രയോഗിച്ചിരുന്ന മറ്റൊരു അക്ഷരസമ്പ്രദായവും ഉണ്ടായിരുന്നു. ഇത് ശ്രീലങ്കയിലെ പാലി ഹസ്തലിഖിതങ്ങളിലാണ് കണ്ടെത്തിയിട്ടുള്ളത്. പന്ത്രണ്ട് സ്വരങ്ങളും 34 വ്യഞ്ജനങ്ങളും ഉപയോഗിച്ചുകൊണ്ടുള്ള മറ്റൊരു സമ്പ്രദായവുമുണ്ട്, പാലി കയ്യെഴുത്തു പ്രതികളില്. ഇതില് ക, കാ, .... എന്നിങ്ങനെ 13 മുതല് 26 വരെയും തുടര്ന്നും കാണാം. എ.ഡി. 3-ാം ശ.-ത്തിനു മുമ്പുവരെയെങ്കിലും ഈ അക്ഷരസമ്പ്രദായം വടക്കെ ഇന്ത്യയില് ഉപയോഗിച്ചു കണ്ടിട്ടില്ല. | ||
| - | അക്ഷരപല്ലി. പഴയ ഹസ്തലിഖിതങ്ങളില് അക്കങ്ങള്ക്ക് ഉപയോഗിച്ചുകാണുന്ന ശബ്ദങ്ങളുടെ പട്ടിക: | + | '''അക്ഷരപല്ലി'''. പഴയ ഹസ്തലിഖിതങ്ങളില് അക്കങ്ങള്ക്ക് ഉപയോഗിച്ചുകാണുന്ന ശബ്ദങ്ങളുടെ പട്ടിക: |
| - | + | [[Image:pno.27.Akragal.png]] | |
| - | + | ||
| - | + | [[Image:pno.27Akshagal2.png]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | |||
16-ാം ശ. വരെ ജൈനരുടെ ഹസ്തലിഖിതങ്ങളില് അക്ഷരപല്ലി ഉപയോഗിച്ചിരുന്നു. അതിനുശേഷം ദശാംശ-അക്കങ്ങള് പ്രയോഗിച്ചു. അക്ഷരപല്ലിയോട് സാദൃശ്യമുള്ള ഒരു സമ്പ്രദായം കേരളത്തില് നിലനിന്നിരുന്നു: | 16-ാം ശ. വരെ ജൈനരുടെ ഹസ്തലിഖിതങ്ങളില് അക്ഷരപല്ലി ഉപയോഗിച്ചിരുന്നു. അതിനുശേഷം ദശാംശ-അക്കങ്ങള് പ്രയോഗിച്ചു. അക്ഷരപല്ലിയോട് സാദൃശ്യമുള്ള ഒരു സമ്പ്രദായം കേരളത്തില് നിലനിന്നിരുന്നു: | ||
| വരി 243: | വരി 190: | ||
നോ: അങ്കപല്ലി, അക്ഷരപല്ലി | നോ: അങ്കപല്ലി, അക്ഷരപല്ലി | ||
| - | പൂജ്യമെന്ന ആശയം. മയന്കാരും ബാബിലോണിയക്കാരും | + | '''പൂജ്യമെന്ന ആശയം'''. മയന്കാരും ബാബിലോണിയക്കാരും ഗണിതസൗകര്യമുള്ള തരത്തിലല്ല അക്കങ്ങള് അംഗീകരിച്ചത്. യഥാക്രമം 20-ഉം 60-ഉം വരെയുള്ള അക്കങ്ങള്ക്ക് ഒറ്റചിഹ്നങ്ങള് അവര്ക്കുണ്ടായിരുന്നില്ലെന്നതാണ് അതിനു കാരണം. ഇന്ത്യയിലാണ് ഈ വഴിക്കുള്ള പുരോഗതിയുണ്ടായത്. ഇന്നു പാശ്ചാത്യ രാജ്യങ്ങളില് ഉപയോഗത്തിലിരിക്കുന്നവിധം പൂജ്യം ആദ്യം പ്രയോഗിച്ചതും ഇന്ത്യക്കാര് തന്നെയാണ്. ഏകദേശം എ.ഡി. 1-ാം ശ.-ത്തില് ഗുജറാത്തിലാണ് പൂജ്യത്തിന് ഒരു പ്രതീകം കണ്ടെത്തിയതെന്നതിന് ചില രേഖകളുണ്ട്. 'ശൂന്യ'മെന്ന് വ്യവഹരിക്കപ്പെടുന്ന പൂജ്യത്തിന് ചിഹ്നമായി ബിന്ദു ആണോ വൃത്തം ആണോ ആദ്യം ഉപയോഗിച്ചതെന്ന് വ്യക്തമല്ല. എ.ഡി. 800-ല് അറബികള് 'സിഫര്' എന്നും പിന്നീട് 'സൈഫര്' എന്നും പേരിട്ട് അതു പകര്ത്തി. 1200-ലാണ് അത് ലത്തീനില് എത്തിയത്. പൂജ്യത്തിന്റെ കണ്ടുപിടിത്തം ഗണിതത്തിലെ ഒരു നിര്ണായക സംഭവമാണ്. |
| - | ( | + | (i) '''പൂജ്യം ഇന്ത്യയില്'''. ബി.സി. 200-നു മുമ്പുതന്നെ പിംഗളന് എന്ന ഗണിതശാസ്ത്രജ്ഞന് ചാന്ദ്രസൂത്രം എന്ന ഗ്രന്ഥത്തില് പൂജ്യത്തിന് 0 എന്ന ചിഹ്നം അളവുകളില് ഉപയോഗിച്ചിരുന്നു. ബി.സി. 200-നു മുമ്പുതന്നെ ഇന്ത്യയില് ഈ ചിഹ്നം ഉണ്ടായിരുന്നു എന്നതിന് ഇതു തെളിവാണ്. ഏകദേശം ഇതേ കാലഘട്ടത്തിലെ ബക്ഷാലി ഹസ്തലിഖിതങ്ങളിലും പൂജ്യത്തിന് 0 എന്ന ചിഹ്നം ഉപയോഗിച്ചിട്ടുണ്ട്. പഞ്ചസിദ്ധാന്തിക (505) എന്ന ജ്യോതിശ്ശാസ്ത്രഗ്രന്ഥത്തില് (0) പൂജ്യത്തെ പല സന്ദര്ഭങ്ങളിലും പരാമര്ശിക്കുന്നുണ്ട്. വരാഹമിഹിരന്റെ സമകാലികനായിരുന്ന ജിനഭദ്രഗണിയുടെ (529-589) ഗ്രന്ഥങ്ങളില് പൂജ്യത്തിന്റെ ചിഹ്നം ഒരു അക്കമെന്ന നിലയില് കൈകാര്യം ചെയ്തു കാണുന്നു. ഭാസ്കരാചാര്യന് I (522) മഹാഭാസ്കരീയം എന്ന ഗ്രന്ഥത്തില് പൂജ്യത്തെ മറ്റു സംഖ്യകളില്നിന്ന് കുറയ്ക്കുന്ന സമ്പ്രദായം വിവരിക്കുന്നുണ്ട്. പൂജ്യചിഹ്നം ഉപയോഗിച്ച് ആര്യഭടീയത്തില് അക്കങ്ങളുടെ സ്ഥാനക്രമസമ്പ്രദായം ഉപയോഗിച്ചു കാണാം. സിദ്ധസേനഗണി (6-ാം ശ.) പൂജ്യം ഉപയോഗിച്ചിരുന്നതായി ചില വ്യാഖ്യാനഗ്രന്ഥങ്ങളില് നിന്നു മനസിലാക്കാം. ഇന്ത്യയിലെ എല്ലാ ഗണിതശാസ്ത്ര ഗ്രന്ഥങ്ങളിലും പൂജ്യം കൊണ്ടുള്ള ഗണിതപ്രക്രിയകള് വിവരിച്ചിട്ടുണ്ട്. ഇവിടെയെല്ലാം ഏതെങ്കിലും ഒരു ചിഹ്നം പൂജ്യത്തിനുപയോഗിച്ചിട്ടുമുണ്ട്. |
പൂജ്യത്തിന് ഉപയോഗിച്ചിരുന്ന ചിഹ്നം വിവിധ രൂപങ്ങളില് ആയിരുന്നു. ബക്ഷാലി കൈയെഴുത്തുപ്രതിയില് ഒരു ബിന്ദു ആണ് ഉപയോഗിച്ചിരുന്നത്. എ.ഡി. 3-ാം ശ.-ത്തിലെ ഈ രേഖയില് ബിന്ദുതന്നെയാണോ എന്ന് പിന്നീട് ലഭ്യമായിട്ടുള്ള (9-ാം ശ.-ത്തില്) പ്രതികളില്നിന്നുമാത്രം നിശ്ചയിക്കാവുന്നതല്ല. 6-ാം ശ.-ത്തിന്റെ അവസാനകാലത്ത് ജീവിച്ചിരുന്ന സുബന്ധു എന്ന ഗണിതശാസ്ത്രജ്ഞന്റെ വാസവദത്ത എന്ന ഗ്രന്ഥത്തില് നിന്ന് ബിന്ദു പൂജ്യത്തെ സൂചിപ്പിച്ചിരുന്നതായി മനസിലാക്കാം. ഒരു ബിന്ദു ഒരു സംഖ്യയെ പത്തിരട്ടിയാക്കുന്നതുപോലെ '....' എന്നു ഹിന്ദി കവി ബിഹാരിലാല് (1595-1663?) പ്രയോഗിച്ചിട്ടുണ്ട്. | പൂജ്യത്തിന് ഉപയോഗിച്ചിരുന്ന ചിഹ്നം വിവിധ രൂപങ്ങളില് ആയിരുന്നു. ബക്ഷാലി കൈയെഴുത്തുപ്രതിയില് ഒരു ബിന്ദു ആണ് ഉപയോഗിച്ചിരുന്നത്. എ.ഡി. 3-ാം ശ.-ത്തിലെ ഈ രേഖയില് ബിന്ദുതന്നെയാണോ എന്ന് പിന്നീട് ലഭ്യമായിട്ടുള്ള (9-ാം ശ.-ത്തില്) പ്രതികളില്നിന്നുമാത്രം നിശ്ചയിക്കാവുന്നതല്ല. 6-ാം ശ.-ത്തിന്റെ അവസാനകാലത്ത് ജീവിച്ചിരുന്ന സുബന്ധു എന്ന ഗണിതശാസ്ത്രജ്ഞന്റെ വാസവദത്ത എന്ന ഗ്രന്ഥത്തില് നിന്ന് ബിന്ദു പൂജ്യത്തെ സൂചിപ്പിച്ചിരുന്നതായി മനസിലാക്കാം. ഒരു ബിന്ദു ഒരു സംഖ്യയെ പത്തിരട്ടിയാക്കുന്നതുപോലെ '....' എന്നു ഹിന്ദി കവി ബിഹാരിലാല് (1595-1663?) പ്രയോഗിച്ചിട്ടുണ്ട്. | ||
| - | 8-ാം ശ.-ത്തിലെ | + | 8-ാം ശ.-ത്തിലെ ജയ്വര്ധന് II-ന്റെ രഘോളിത്തകിടുകള് (Ragholi Plates) ആണ് പൂജ്യത്തിന് ചെറിയ വൃത്തം (o) അക്കമായി ഉപയോഗിച്ചിരുന്നതിന്റെ, ലഭ്യമായ ഏറ്റവും പ്രാചീനരേഖ. ഭോജദേവന്റെ ഗ്വാളിയര് ലിഖിതങ്ങളില് ചെറുവൃത്തം പൂജ്യചിഹ്നമായി ഉപയോഗിച്ചു കാണുന്നു. 8-ാം ശ.-ത്തിനു മുമ്പു മുതല് ചെറുവൃത്തം പൂജ്യചിഹ്നമായി ഉപയോഗിച്ചിരുന്നുവെന്നു നിശ്ചയിക്കാം. |
.... 0 0 0 0 0 ഇങ്ങനെ എഴുതി ഇടത്തുനിന്നു വലത്തോട്ട് ആദ്യത്തെ പൂജ്യം തൊട്ട് ഒന്ന്, പത്ത്, നൂറ്, ആയിരം, .... എന്നിങ്ങനെ സ്ഥാനക്രമം പറയുന്ന സമ്പ്രദായം ഭാസ്കരാചാര്യന് ക-ന്റെ കാലത്തും ഉണ്ടായിരുന്നു. അങ്കഗണിതത്തെ സംബന്ധിച്ച (പാടിഗണിതം) എല്ലാ ഗ്രന്ഥങ്ങളിലും അറിയാത്തതിനെ സൂചിപ്പിക്കുന്ന ചിഹ്നമായി 0 ഉപയോഗിച്ചിരുന്നു. എ.ഡി. 3-ാം ശ.-ത്തിലാണ് പൂജ്യത്തിന്റെ ഈ ഉപയോഗം കണ്ടെത്തിയത്. ബക്ഷാലി ഹസ്തലിഖിതത്തിലും ഇങ്ങനെ പൂജ്യം ഉപയോഗിച്ചിട്ടുണ്ട്. അക്കം ഇല്ല എന്നു സൂചിപ്പിക്കയാണ് 0 എന്ന ചിഹ്നം കൊണ്ടുദ്ദേശിച്ചിട്ടുള്ളത്. | .... 0 0 0 0 0 ഇങ്ങനെ എഴുതി ഇടത്തുനിന്നു വലത്തോട്ട് ആദ്യത്തെ പൂജ്യം തൊട്ട് ഒന്ന്, പത്ത്, നൂറ്, ആയിരം, .... എന്നിങ്ങനെ സ്ഥാനക്രമം പറയുന്ന സമ്പ്രദായം ഭാസ്കരാചാര്യന് ക-ന്റെ കാലത്തും ഉണ്ടായിരുന്നു. അങ്കഗണിതത്തെ സംബന്ധിച്ച (പാടിഗണിതം) എല്ലാ ഗ്രന്ഥങ്ങളിലും അറിയാത്തതിനെ സൂചിപ്പിക്കുന്ന ചിഹ്നമായി 0 ഉപയോഗിച്ചിരുന്നു. എ.ഡി. 3-ാം ശ.-ത്തിലാണ് പൂജ്യത്തിന്റെ ഈ ഉപയോഗം കണ്ടെത്തിയത്. ബക്ഷാലി ഹസ്തലിഖിതത്തിലും ഇങ്ങനെ പൂജ്യം ഉപയോഗിച്ചിട്ടുണ്ട്. അക്കം ഇല്ല എന്നു സൂചിപ്പിക്കയാണ് 0 എന്ന ചിഹ്നം കൊണ്ടുദ്ദേശിച്ചിട്ടുള്ളത്. | ||
| - | (ii) പൂജ്യത്തിന്റെ ഗണിതം. പൂജ്യത്തിന്റെ എല്ലാ പ്രയോഗങ്ങളും ഇന്ത്യയില് ഉണ്ടായിരുന്നു. മറ്റു സംഖ്യകളോടൊപ്പം പൂജ്യത്തെയും ഇന്ത്യയില് അക്കം എന്ന നിലയില് അംഗീകരിച്ചിരുന്നു. | + | (ii) '''പൂജ്യത്തിന്റെ ഗണിതം'''. പൂജ്യത്തിന്റെ എല്ലാ പ്രയോഗങ്ങളും ഇന്ത്യയില് ഉണ്ടായിരുന്നു. മറ്റു സംഖ്യകളോടൊപ്പം പൂജ്യത്തെയും ഇന്ത്യയില് അക്കം എന്ന നിലയില് അംഗീകരിച്ചിരുന്നു. |
| + | [[Image:pno28BB11.png]] | ||
| + | |||
| + | [[Image:pno.28.Bha12.png]] | ||
| + | |||
'പൂജ്യം', 'ശൂന്യം' (0) എന്ന് പറയുന്ന ചിഹ്നം സ്വയം നിന്നാല് ഒരു സംഖ്യയേയും സൂചിപ്പിക്കുന്നില്ല. എന്നാല് ഒരുപൂര്ണസംഖ്യയുടെ ഒടുവില് പൂജ്യം വന്നാല് അതിന്റെ മൂല്യത്തെ ഇത് പത്തുമടങ്ങ് വര്ധിപ്പിക്കുന്നു. അതുപോലെ, ദശാംശഭിന്നങ്ങളില് ഇടത്തെ അറ്റത്ത് വരുന്ന പൂജ്യം സംഖ്യാമൂല്യത്തെ പത്തിലൊന്നായി കുറയ്ക്കുകയും ചെയ്യുന്നു. | 'പൂജ്യം', 'ശൂന്യം' (0) എന്ന് പറയുന്ന ചിഹ്നം സ്വയം നിന്നാല് ഒരു സംഖ്യയേയും സൂചിപ്പിക്കുന്നില്ല. എന്നാല് ഒരുപൂര്ണസംഖ്യയുടെ ഒടുവില് പൂജ്യം വന്നാല് അതിന്റെ മൂല്യത്തെ ഇത് പത്തുമടങ്ങ് വര്ധിപ്പിക്കുന്നു. അതുപോലെ, ദശാംശഭിന്നങ്ങളില് ഇടത്തെ അറ്റത്ത് വരുന്ന പൂജ്യം സംഖ്യാമൂല്യത്തെ പത്തിലൊന്നായി കുറയ്ക്കുകയും ചെയ്യുന്നു. | ||
വരാഹമിഹിരന്റെ പഞ്ചസിദ്ധാന്തിക എന്ന ജ്യോതിഃശാസ്ത്രഗ്രന്ഥത്തില് പൂജ്യംകൊണ്ടുള്ള സങ്കലനവും വ്യവകലനവും സാന്ദര്ഭികമായി പ്രതിപാദിച്ചിട്ടുണ്ട്. ദശാംശഗണിതം മുഴുവനും ആര്യഭടീയവ്യാഖ്യാനത്തില് ഭാസ്കരാചാര്യന് 1 (522) ചേര്ത്തിരിക്കുന്നു. ബ്രഹ്മഗുപ്തന്റെ ഗ്രന്ഥത്തിലും (628) പിന്നീടുള്ള മറ്റു ഗണിത ഗ്രന്ഥങ്ങളിലും പൂജ്യം കൊണ്ടുള്ള ക്രിയകള് വിവരിച്ചുകാണാം. അങ്കഗണിതത്തിലും (Arithmetic) ബീജഗണിതത്തിലും (Algebra) വ്യത്യസ്ത രീതിയിലാണ് പൂജ്യം കൈകാര്യം ചെയ്തിരിക്കുന്നത്. | വരാഹമിഹിരന്റെ പഞ്ചസിദ്ധാന്തിക എന്ന ജ്യോതിഃശാസ്ത്രഗ്രന്ഥത്തില് പൂജ്യംകൊണ്ടുള്ള സങ്കലനവും വ്യവകലനവും സാന്ദര്ഭികമായി പ്രതിപാദിച്ചിട്ടുണ്ട്. ദശാംശഗണിതം മുഴുവനും ആര്യഭടീയവ്യാഖ്യാനത്തില് ഭാസ്കരാചാര്യന് 1 (522) ചേര്ത്തിരിക്കുന്നു. ബ്രഹ്മഗുപ്തന്റെ ഗ്രന്ഥത്തിലും (628) പിന്നീടുള്ള മറ്റു ഗണിത ഗ്രന്ഥങ്ങളിലും പൂജ്യം കൊണ്ടുള്ള ക്രിയകള് വിവരിച്ചുകാണാം. അങ്കഗണിതത്തിലും (Arithmetic) ബീജഗണിതത്തിലും (Algebra) വ്യത്യസ്ത രീതിയിലാണ് പൂജ്യം കൈകാര്യം ചെയ്തിരിക്കുന്നത്. | ||
| - | + | അങ്കഗണിതത്തില്, ഒരു സംഖ്യയില് നിന്ന് അതേ സംഖ്യകുറച്ചാല് കിട്ടുന്ന ഫലത്തെയാണ് പൂജ്യമെന്നു നിര്വചിച്ചിരിക്കുന്നത്. പൂജ്യംകൊണ്ട് സങ്കലനം, വ്യവകലനം, ഗുണനം എന്നിവ നടത്താമെന്നും ഹരണം നടത്തരുതെന്നും അങ്കഗണിതത്തില് നിര്ദേശിച്ചിട്ടുണ്ട്. ഒരു സംഖ്യയോട് പൂജ്യം കൂട്ടിയാല് ഫലം ആ സംഖ്യ തന്നെ; ഒരു സംഖ്യയില് നിന്നു പൂജ്യം കുറച്ചാലും ഫലം ആ സംഖ്യതന്നെ; ഒരു സംഖ്യയെ പൂജ്യം കൊണ്ടു ഗുണിച്ചാല് ഫലം പൂജ്യമാണ്. ശ്രീധരാചാര്യനും ആര്യഭടന് II-നും (മഹാസിദ്ധാന്താ) നാരായണാചാര്യനും (പാടിഗണിതം) മഹാവീരാചാര്യനും (ഗണിതസാരസംഗ്രഹം) ഇക്കാര്യങ്ങള് വിവരിക്കുന്നുണ്ട്. ഒരു സംഖ്യയെ പൂജ്യംകൊണ്ടു ഹരിച്ചാല് ഫലം ആ സംഖ്യതന്നെയെന്ന് മഹാവീരന് പ്രസ്താവിച്ചിരിക്കുന്നത് അബദ്ധമാണ്. എന്നാല് മഹാവീരനു രണ്ടു നൂറ്റാണ്ടുകള്ക്കു മുമ്പുതന്നെ ബ്രഹ്മഗുപ്തന് ശരിയായ ഉത്തരം അതിനു നല്കിയിരിക്കെ മഹാവീരന് ഈ തെറ്റു പറ്റിയത് വിചിത്രമായിരിക്കുന്നു. | |
| - | + | ||
| - | അങ്കഗണിതത്തില്, ഒരു സംഖ്യയില് നിന്ന് അതേ സംഖ്യകുറച്ചാല് കിട്ടുന്ന ഫലത്തെയാണ് പൂജ്യമെന്നു നിര്വചിച്ചിരിക്കുന്നത്. പൂജ്യംകൊണ്ട് സങ്കലനം, വ്യവകലനം, ഗുണനം എന്നിവ നടത്താമെന്നും ഹരണം നടത്തരുതെന്നും അങ്കഗണിതത്തില് നിര്ദേശിച്ചിട്ടുണ്ട്. ഒരു സംഖ്യയോട് പൂജ്യം കൂട്ടിയാല് ഫലം ആ സംഖ്യ തന്നെ; ഒരു സംഖ്യയില് നിന്നു പൂജ്യം കുറച്ചാലും ഫലം ആ സംഖ്യതന്നെ; ഒരു സംഖ്യയെ പൂജ്യം കൊണ്ടു ഗുണിച്ചാല് ഫലം പൂജ്യമാണ്. ശ്രീധരാചാര്യനും ആര്യഭടന് | + | |
ബ്രഹ്മസ്ഫുടസിദ്ധാന്തത്തിലാണ് (628) പൂജ്യത്തെ ബീജീയാങ്കമെന്ന നിലയില് ആദ്യമായി കൈകാര്യം ചെയ്തിരിക്കുന്നത്. | ബ്രഹ്മസ്ഫുടസിദ്ധാന്തത്തിലാണ് (628) പൂജ്യത്തെ ബീജീയാങ്കമെന്ന നിലയില് ആദ്യമായി കൈകാര്യം ചെയ്തിരിക്കുന്നത്. | ||
| + | |||
ഋണസംഖ്യയില് നിന്നു പൂജ്യം കുറച്ചാല് ഋണസംഖ്യ തന്നെ ഫലം; ധനസംഖ്യയില് നിന്നാണെങ്കില് ധനസംഖ്യയും; പൂജ്യത്തില്നിന്നാണെങ്കില് പൂജ്യവും. ഋണസംഖ്യയും പൂജ്യവും തമ്മിലോ ധനസംഖ്യയും പൂജ്യവും തമ്മിലോ ഗുണിച്ചാല് പൂജ്യമാണ് ഫലം; പൂജ്യങ്ങള് തമ്മിലായാലും പൂജ്യം തന്നെ. | ഋണസംഖ്യയില് നിന്നു പൂജ്യം കുറച്ചാല് ഋണസംഖ്യ തന്നെ ഫലം; ധനസംഖ്യയില് നിന്നാണെങ്കില് ധനസംഖ്യയും; പൂജ്യത്തില്നിന്നാണെങ്കില് പൂജ്യവും. ഋണസംഖ്യയും പൂജ്യവും തമ്മിലോ ധനസംഖ്യയും പൂജ്യവും തമ്മിലോ ഗുണിച്ചാല് പൂജ്യമാണ് ഫലം; പൂജ്യങ്ങള് തമ്മിലായാലും പൂജ്യം തന്നെ. | ||
| - | ഭാസ്കരാചാര്യന് | + | ഭാസ്കരാചാര്യന് II ലീലാവതി എന്ന ഗ്രന്ഥത്തിലും ഇത്തരം നിഗമനങ്ങള് പൂജ്യത്തെക്കുറിച്ച് ചേര്ത്തിട്ടുണ്ട്. പൂജ്യം ഒരു അനന്തസൂക്ഷ്മമായി (Infinitesimal) ബ്രഹ്മഗുപ്താചാര്യന് ഉപയോഗിച്ചിട്ടുണ്ട്. x ÷ 0, 0 ÷ x എന്നിവ x/0, 0/x എന്നിങ്ങനെ എഴുതാം. ഭാസ്കരാചാര്യന് II ഈ അര്ഥത്തില് പൂജ്യത്തെ കലനത്തില് (Calculus) പ്രകടമായി പ്രയോഗിച്ചിട്ടുണ്ട്. x/0 = α(അനന്തം), α+ k = α എന്നീ ഫലഭാഗങ്ങളും അദ്ദേഹത്തിനു വശമായിരുന്നു. = 0 എന്ന് തെറ്റായി ബ്രഹ്മഗുപ്തന് പ്രസ്താവിച്ചിട്ടുള്ളത് ഭാസ്കരാചാര്യന് 11 സീമാസിദ്ധാന്തം (Limit theory) ഉപയോഗിച്ച് തിരുത്തിയിട്ടുണ്ട്. |
| - | + | [[Image:pno28ff1.png]] | |
| - | ആധുനിക സമ്പ്രദായം. ആധുനിക അക്കസമ്പ്രദായത്തിന്റെ ഉറവിടം ഇന്ത്യയിലാണെന്ന് പറയാം. അറബിക് അക്കങ്ങളെന്നു പറയുന്നത് അത്ര ശരിയല്ല. ചരിത്രരേഖകള് വച്ചുനോക്കിയാല് 1, 4, 6 എന്നിവ അശോകന്റെ ശാസനങ്ങളിലും (ബി.സി. 3-ാം ശ.) 2, 4, 6, 7, 9 എന്നിവ നാനാഘട് ശാസനങ്ങളിലും (ബി.സി. 2-ാം ശ.) 2, 3, 4, 5, 6, 7, 9 നാസിക് ശാസനങ്ങളിലും (എ.ഡി. ഒന്നും രണ്ടും ശ.-ങ്ങള്) കാണാം. മെസപ്പൊട്ടേമിയയിലെ ഒരു മെത്രാനായിരുന്ന സെവേരസ് സെബോക്ടിന്റെ ഒരു രേഖയില് നിന്നാണ് 'ഹിന്ദുഅക്ക'ങ്ങളെക്കുറിച്ചുള്ള ആദ്യത്തെ പരാമര്ശം പാശ്ചാത്യര്ക്കു കിട്ടുന്നത്. എ.ഡി. 8-ാം ശ.-ത്തിന്റെ അവസാനത്തില് ചില ഭാരതീയ ജ്യോതിഃശാസ്ത്ര ഗ്രന്ഥങ്ങളുടെ പരാവര്ത്തനങ്ങള് അറേബ്യയില് ഉണ്ടായി. അറബി പണ്ഡിതന്മാര്ക്ക് ഇന്ത്യന് അക്കങ്ങള് പരിചിതമായിരുന്നു. എ.ഡി. 825-ല് അല്-ഖവാരിസ്മി ഇതേപ്പറ്റി ഒരു ബൃഹദ്ഗ്രന്ഥം തന്നെ അറബി ഭാഷയില് രചിച്ചിട്ടുണ്ട്. ഇതിന്റെ പരിഭാഷയും പാശ്ചാത്യര്ക്കു കിട്ടി. എ.ഡി. 976-ല് സ്പെയിന് ഭാഷയില് എഴുതിയ ഒരു ഗ്രന്ഥമാണ് ഇക്കാര്യത്തില് യൂറോപ്പുകാരുടെ പ്രമാണം. അറബിവഴിയല്ലാതെ തന്നെ യൂറോപ്പില് ഇന്ത്യന് അക്കങ്ങള് എത്തിയിരുന്നു. | + | '''ആധുനിക സമ്പ്രദായം'''. ആധുനിക അക്കസമ്പ്രദായത്തിന്റെ ഉറവിടം ഇന്ത്യയിലാണെന്ന് പറയാം. അറബിക് അക്കങ്ങളെന്നു പറയുന്നത് അത്ര ശരിയല്ല. ചരിത്രരേഖകള് വച്ചുനോക്കിയാല് 1, 4, 6 എന്നിവ അശോകന്റെ ശാസനങ്ങളിലും (ബി.സി. 3-ാം ശ.) 2, 4, 6, 7, 9 എന്നിവ നാനാഘട് ശാസനങ്ങളിലും (ബി.സി. 2-ാം ശ.) 2, 3, 4, 5, 6, 7, 9 നാസിക് ശാസനങ്ങളിലും (എ.ഡി. ഒന്നും രണ്ടും ശ.-ങ്ങള്) കാണാം. മെസപ്പൊട്ടേമിയയിലെ ഒരു മെത്രാനായിരുന്ന സെവേരസ് സെബോക്ടിന്റെ ഒരു രേഖയില് നിന്നാണ് 'ഹിന്ദുഅക്ക'ങ്ങളെക്കുറിച്ചുള്ള ആദ്യത്തെ പരാമര്ശം പാശ്ചാത്യര്ക്കു കിട്ടുന്നത്. എ.ഡി. 8-ാം ശ.-ത്തിന്റെ അവസാനത്തില് ചില ഭാരതീയ ജ്യോതിഃശാസ്ത്ര ഗ്രന്ഥങ്ങളുടെ പരാവര്ത്തനങ്ങള് അറേബ്യയില് ഉണ്ടായി. അറബി പണ്ഡിതന്മാര്ക്ക് ഇന്ത്യന് അക്കങ്ങള് പരിചിതമായിരുന്നു. എ.ഡി. 825-ല് അല്-ഖവാരിസ്മി ഇതേപ്പറ്റി ഒരു ബൃഹദ്ഗ്രന്ഥം തന്നെ അറബി ഭാഷയില് രചിച്ചിട്ടുണ്ട്. ഇതിന്റെ പരിഭാഷയും പാശ്ചാത്യര്ക്കു കിട്ടി. എ.ഡി. 976-ല് സ്പെയിന് ഭാഷയില് എഴുതിയ ഒരു ഗ്രന്ഥമാണ് ഇക്കാര്യത്തില് യൂറോപ്പുകാരുടെ പ്രമാണം. അറബിവഴിയല്ലാതെ തന്നെ യൂറോപ്പില് ഇന്ത്യന് അക്കങ്ങള് എത്തിയിരുന്നു. |
പത്ത് ആധാരമാക്കിക്കൊണ്ടുള്ള അക്കസമ്പ്രദായം ഇന്ന് അന്താരാഷ്ട്ര ഗണിതഭാഷയായിത്തീര്ന്നിരിക്കുകയാണ്. എങ്കിലും ചൈനീസ്, ജപ്പാന്, റഷ്യന്, ഇംഗ്ളീഷ്, ജര്മന്, ഗ്രീക് എന്നീ ഭാഷകളില് പ്രചാരമുള്ളത് രണ്ട് ആധാരമാക്കിക്കൊണ്ടുള്ള പദ്ധതിയാണ് (ദ്വയാംഗ സമ്പ്രദായം). ഇലക്ട്രോണിക് കംപ്യൂട്ടറുകളില് പ്രയോഗിക്കുന്നതും ഈ പദ്ധതി തന്നെ. യാന്ത്രിക സ്വഭാവത്തിനനുയോജ്യമായി വിജ്ഞാനം 'പരാവര്ത്തനം' ചെയ്യുവാന് ഉതകുന്ന ഏറ്റവും എളുപ്പമുള്ള സമ്പ്രദായം ഈ ദ്വയാങ്കപദ്ധതിയാണ്. ഇതില് 0, 1 എന്നീ ചിഹ്നങ്ങള് മാത്രമേ ആവശ്യമുള്ളു. സംഖ്യകള് ഈ സമ്പ്രദായത്തില് രേഖപ്പെടുത്തുന്ന രീതി താഴെ ചേര്ക്കുന്നു. | പത്ത് ആധാരമാക്കിക്കൊണ്ടുള്ള അക്കസമ്പ്രദായം ഇന്ന് അന്താരാഷ്ട്ര ഗണിതഭാഷയായിത്തീര്ന്നിരിക്കുകയാണ്. എങ്കിലും ചൈനീസ്, ജപ്പാന്, റഷ്യന്, ഇംഗ്ളീഷ്, ജര്മന്, ഗ്രീക് എന്നീ ഭാഷകളില് പ്രചാരമുള്ളത് രണ്ട് ആധാരമാക്കിക്കൊണ്ടുള്ള പദ്ധതിയാണ് (ദ്വയാംഗ സമ്പ്രദായം). ഇലക്ട്രോണിക് കംപ്യൂട്ടറുകളില് പ്രയോഗിക്കുന്നതും ഈ പദ്ധതി തന്നെ. യാന്ത്രിക സ്വഭാവത്തിനനുയോജ്യമായി വിജ്ഞാനം 'പരാവര്ത്തനം' ചെയ്യുവാന് ഉതകുന്ന ഏറ്റവും എളുപ്പമുള്ള സമ്പ്രദായം ഈ ദ്വയാങ്കപദ്ധതിയാണ്. ഇതില് 0, 1 എന്നീ ചിഹ്നങ്ങള് മാത്രമേ ആവശ്യമുള്ളു. സംഖ്യകള് ഈ സമ്പ്രദായത്തില് രേഖപ്പെടുത്തുന്ന രീതി താഴെ ചേര്ക്കുന്നു. | ||
| - | + | [[Image:pno29 ff.png]] | |
| - | + | ||
| - | + | ||
| - | + | ||
നോ: അക്ഷരസംഖ്യ; അങ്കഗണിതം; കംപ്യൂട്ടര്; കലിസംഖ്യ; പരല്പേര്; സംഖ്യകള് | നോ: അക്ഷരസംഖ്യ; അങ്കഗണിതം; കംപ്യൂട്ടര്; കലിസംഖ്യ; പരല്പേര്; സംഖ്യകള് | ||
| + | [[Category:ഗണിതം]] | ||
Current revision as of 03:36, 11 നവംബര് 2014
അക്കങ്ങള്
Numerals
സംഖ്യകള് രേഖപ്പെടുത്തുന്നതിനുള്ള ചിഹ്നങ്ങള്. അതിപ്രാചീന കാലങ്ങളില്തന്നെ ഒരു ജീവിതാവശ്യമെന്ന നിലയില് മനുഷ്യന് എണ്ണാന് പഠിച്ചു. പിന്നെയും വളരെക്കാലം കഴിഞ്ഞിട്ടാണ് അക്കങ്ങള് ഉപയോഗിക്കാന് തുടങ്ങിയത്. എണ്ണം രേഖപ്പെടുത്താന് കല്ലും കമ്പും ഒരുപക്ഷേ അവന് ഉപയോഗിച്ചിരിക്കാം. പ്രാചീന രേഖകളനുസരിച്ച് കല്ലിലോ, വടിയിലോ അടയാളപ്പെടുത്തിയാണ് അക്കം എഴുതിയിരുന്നതെന്ന് കാണാം. അക്കം എഴുതേണ്ട ആവശ്യംതന്നെ അന്നുണ്ടായിരുന്നില്ല. സാധനങ്ങള് പരസ്പരം കൈമാറി ആവശ്യം നിറവേറ്റുന്ന വിനിമയ (Barter) സമ്പ്രദായമായിരുന്നു നിലവിലിരുന്നത്. ഏതാനും ശബ്ദങ്ങള് പുറപ്പെടുവിച്ച് എണ്ണം കുറിക്കുന്ന സമ്പ്രദായം വന്നതിനുശേഷമാകാം എഴുത്തുതുടങ്ങിയത്. ചെറിയ എണ്ണങ്ങള് സൂചിപ്പിക്കാന് ശബ്ദത്തിലൂടെ എളുപ്പത്തില് സാധിച്ചെങ്കിലും വലിയ എണ്ണങ്ങള് ആവശ്യമായി വന്നപ്പോള് എഴുതിവയ്ക്കാതെ നിവൃത്തിയില്ലാതായി.
ചരിത്രം. ഈജിപ്ത്, ക്രീറ്റ്, സുമേറിയ, ഇന്ത്യ, ചൈന എന്നിവിടങ്ങളിലാണ് അക്കമെഴുത്ത് ആരംഭിച്ചത്. ഈജിപ്തിലും ക്രീറ്റിലും സുമേറിയയിലും മറ്റും ചിത്രലിപികള് ഉപയോഗിച്ചിരുന്നതായി പ്രാചീന രേഖകള് തെളിയിക്കുന്നു. ഏകദേശം ബി.സി. 3400-ല് ഈജിപ്തിലും 3000-ല് സുമേറിയയിലും 1200-ല് ക്രീറ്റിലും ഒന്ന്, പത്ത് എന്നിവ യഥാക്രമം ![]() എന്നീ രൂപത്തിലെഴുതിയിരുന്നു.
എന്നീ രൂപത്തിലെഴുതിയിരുന്നു.
പത്ത് അടിസ്ഥാനമാക്കിക്കൊണ്ടുള്ള അക്കങ്ങള്ക്കാണ് ഏറ്റവും പഴക്കമുള്ളത്. ഒരുപക്ഷേ മനുഷ്യന്റെ കൈവിരലുകളുടെ എണ്ണമായതിനാലാവാം പത്തിന് ഈ പ്രാധാന്യം വന്നത്. പത്ത് അടിസ്ഥാനമാക്കിയാണ് ഇംഗ്ളീഷില് എണ്ണങ്ങള്ക്കു പേരുകള് വന്നിട്ടുള്ളത്. പത്തു കൂടാത്ത മറ്റു സംഖ്യകളും ഉപയോഗിക്കാറുണ്ട്. ആസ്റ്റ്രേലിയയിലെ അതിപ്രാചീന വര്ഗക്കാരും ന്യൂഗിനിയുടെ പരിസരങ്ങളിലും റ്റോറസ് പ്രദേശത്തും ചില പാപ്പുവന് (papuan) ഭാഷക്കാരും ആഫ്രിക്കന് പിഗ്മികളും അനവധി തെക്കെ അമേരിക്കന് വര്ഗക്കാരും 'രണ്ട്' ആണ് ആധാരമായി സ്വീകരിച്ചത്. ടൈറാഡെല് ഫ്യൂഗോ വര്ഗക്കാരും തെക്കെ അമേരിക്കന് വന്കരയിലുള്ളവരും മൂന്ന്, നാല് എന്നിവയെ ആധാരമാക്കി എണ്ണം കുറിച്ചിരുന്നു. അഞ്ച് വളരെ പ്രാചീന കാലത്തുതന്നെ സ്വീകൃതമായിരുന്നു. തെക്കേ അമേരിക്കയിലെ ഒരു ആരാവാക്കന് ഭാഷയായ സാരാവെക്കിയില് മാത്രമാണ് ഇന്നും 'അഞ്ച്' ആധാരമായി ഉപയോഗിച്ചു കാണുന്നത്. മറ്റു ചിലേടത്ത് 'പത്തും' 'ഇരുപതും' ആധാരമായി സ്വീകരിച്ചുകാണുന്നു. ആഫ്രിക്കയുടെ വടക്കുപടിഞ്ഞാറന് പ്രദേശങ്ങളില് ആറും പന്ത്രണ്ടും പ്രയോഗിച്ചിരിക്കുന്നതുകാണാം. മെക്സിക്കോ, മധ്യാഫ്രിക്ക എന്നിവിടങ്ങളൊഴിച്ചാല് മറ്റു മിക്ക രാജ്യങ്ങളിലും ദശസമ്പ്രദായം സ്വീകരിച്ചിരുന്നു. എന്നാലും ദ്വാദശം (12), ജോടി (2) എന്നീ പ്രയോഗങ്ങളിലൂടെ 10 അല്ലാത്ത അടിസ്ഥാനങ്ങളും നടപ്പിലുണ്ടായിരുന്നു എന്നു വ്യക്തമാണ്. കോണങ്ങള് അളക്കുമ്പോള് ആധാരമായി 60 സ്വീകരിക്കാറുണ്ട്.
അക്കമെഴുത്ത്. പ്രാകൃത സമ്പ്രദായത്തില് I, II, III, ≡ എന്നോ --, =, .., എന്നോ ആയിരിക്കണം അക്കങ്ങള് പ്രയോഗിച്ചിരുന്നത്. സൈബീരിയയിലെ യുക്കാഗിരന്മാര് ഒന്ന്, രണ്ട്, മൂന്ന്, മൂന്നും ഒന്നും, അഞ്ച്, രണ്ടുമൂന്ന്, രണ്ടു മൂന്നും ഒന്നും, രണ്ടുമൂന്നും രണ്ടും, ഒന്നൊഴികെ പത്ത്, പത്ത് എന്നിങ്ങനെയാണ് എണ്ണിയിരുന്നത്. എളുപ്പമായ രീതിയില് ഗ്രൂപ്പ് ചെയ്ത് അക്കങ്ങളെഴുതുന്ന രീതിയാണ് റോമക്കാരുടേത്. ഉദാ. 19-ന് XIX ഈജിപ്തില് ശിലാലിഖിതങ്ങളിലെ ചിത്രമെഴുത്തുകളിലാണ് ഈ സമ്പ്രദായത്തിന്റെ ആദ്യരൂപങ്ങള് കാണുക.
ഹൈറോഗ്ളിഫിക്സ്. ഈജിപ്തില് വലത്തുനിന്ന് ഇടത്തോട്ടാണ് പഴയ എഴുത്ത്.
2312841 = 2(10)6 + 3(10)5 + 1(10)4 + 2(10)3 + 8 (10)2 + 4 (10) + 1. ഇതെഴുതുന്നത് ഇങ്ങനെയാണ്.
പിരമിഡുകളിലും മറ്റും ഇത്തരം ചിത്രലേഖനങ്ങള് കാണാം.
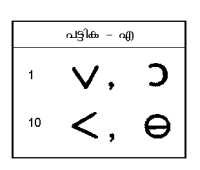
ബാബിലോണിന്റെ പരിസരങ്ങളില് കളിമണ് പലകകളില് എഴുതി ചൂളയ്ക്കുവച്ച് ഉറപ്പുവരുത്തി രേഖകളായി സൂക്ഷിച്ചിട്ടുള്ള ചരിത്രാവശിഷ്ടങ്ങളില് കാണുന്ന ക്യൂനിഫോം (cuniform) സമ്പ്രദായത്തില് 1, 10 എന്നിവയുടെ ചിഹ്നങ്ങള് യഥാക്രമം പട്ടിക എ-യില് ചേര്ത്തിരിക്കുന്നു. 60 വരെയുള്ള എണ്ണങ്ങള്ക്ക് ഈ രൂപങ്ങള് ഉപയോഗിച്ചിരുന്നു.
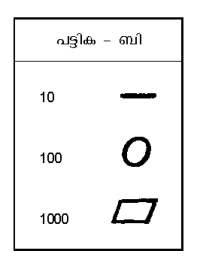
ഗ്രീസില് രണ്ടു സമ്പ്രദായങ്ങളുണ്ടായിരുന്നു. ഒന്നാമതായി, 1 ഒമ്പതു പ്രാവശ്യം ആവര്ത്തിക്കപ്പെടുകയും 10-ന് ഒരു ഒറ്റയടയാളം ചേര്ക്കുകയുമാണ്; രണ്ടാമതായി, എളുപ്പമായ ഗ്രൂപ്പിംഗ് സമ്പ്രദായവും. ഇതിനു മുമ്പുതന്നെ ബാബിലോണിയക്കാരും ഈജിപ്തുകാരും ഫിനീഷ്യക്കാരും 1 ഒമ്പതുവരെ ആവര്ത്തിക്കുന്ന സമ്പ്രദായവും പ്രയോഗിച്ചിരുന്നു. 10, 100, 1000 എന്നിവയുടെ (ക്രീറ്റില് നിലവിലിരുന്ന) ചിഹ്നങ്ങള് ക്രമത്തില് പട്ടിക ബി-യില് ചേര്ത്തിരിക്കുന്നു.വാക്കുകളുടെ ആദ്യക്ഷരങ്ങള് കൊണ്ട് സംഖ്യകള് ചുരുക്കമായി എഴുതുന്ന രീതിയില് നിന്നാണ് പിന്നീട് അക്ഷരസംഖ്യാ സമ്പ്രദായം ഉണ്ടായത്. ഇന്ത്യയിലെ കലി സംഖ്യ (പരല്പേര്) ഇതിനുദാഹരണമാണ്. 5, 10, 100, 1,000, 10,000 എന്നിവ ക്രമത്തില് π (അഥവാ Γ) Δ, H, X, M (അഥവാ MU ) ഉപയോഗിച്ചു. അക്കങ്ങള് 5 നോടു ചേര്ത്ത് കൂട്ടക്കങ്ങളെഴുതി:![]() ഇത്തരത്തില്. 25436 = MM|XHHHHΔΔΔπ1.ബി.സി. മൂന്നും രണ്ടും ശ.-ങ്ങളില് ഈ സമ്പ്രദായം നിലനിന്നിരുന്നതായി ആറ്റിക് ശാസനങ്ങള് വെളിപ്പെടുത്തുന്നു. ഹെറോഡിയാനിക് അക്കങ്ങളെന്നാണ് ഇതിനു പേര്.
ഇത്തരത്തില്. 25436 = MM|XHHHHΔΔΔπ1.ബി.സി. മൂന്നും രണ്ടും ശ.-ങ്ങളില് ഈ സമ്പ്രദായം നിലനിന്നിരുന്നതായി ആറ്റിക് ശാസനങ്ങള് വെളിപ്പെടുത്തുന്നു. ഹെറോഡിയാനിക് അക്കങ്ങളെന്നാണ് ഇതിനു പേര്.
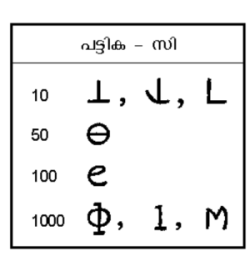
V,X,L,C എന്നീ നാല് അക്കങ്ങള് ഓര്മിച്ചാല് മറ്റെല്ലാം എളുപ്പം എഴുതാവുന്നതിനാലും III, VII എന്നിവ 3, 7 എന്നിവയെക്കാള് എളുപ്പം ഗ്രഹിക്കാവുന്നതായതിനാലും ഏറെക്കാലം ഈ സമ്പ്രദായം നിലനിന്നു. നിവര്ത്തിപ്പിടിച്ച കൈപ്പത്തിയുടെ ആകൃതിയിലുള്ള ചിഹ്നമാണ് V. ഇതുപോലെ രണ്ടെണ്ണമായാല് X എന്നായി; ഇതാണ് പത്ത്; ![]() പിന്നീട് L ആയി 50-ന്; ø (തീറ്റാ), പിന്നീട് C 100 നെയും സൂചിപ്പിച്ചു; ø (ഫൈ), പിന്നീട് I അഥവാ M 1,000 വും 10, 50, 100, 1000 എന്നിവയുടെ ചിഹ്നങ്ങള് ക്രമത്തില് പട്ടിക സി-യില് കാണാം.
പിന്നീട് L ആയി 50-ന്; ø (തീറ്റാ), പിന്നീട് C 100 നെയും സൂചിപ്പിച്ചു; ø (ഫൈ), പിന്നീട് I അഥവാ M 1,000 വും 10, 50, 100, 1000 എന്നിവയുടെ ചിഹ്നങ്ങള് ക്രമത്തില് പട്ടിക സി-യില് കാണാം.
ബി.സി. 260-ല് റോമാക്കാര് കാര്തേജിയന്മാരുടെ മേല് നേടിയ വിജയത്തെ അനുസ്മരിച്ച് സ്ഥാപിക്കപ്പെട്ട സ്തംഭത്തിന്മേല് (Columna Rostrata) കാണുന്ന അക്കങ്ങളാണ് വലിയ സംഖ്യകളുടെ ഏറ്റവും പ്രാചീനമായ രേഖകള്. ഇതില് (((1))) എന്നിങ്ങനെ 23 പ്രാവശ്യം ആവര്ത്തിച്ചു കാണുന്നത് 23,00,000 ആണ്.
ഇതില്നിന്ന് (1) = 1,000, ((1)) = 10,000, (((1))) = 1,00,000 എന്ന് ഊഹിക്കാം. അച്ചടി സാധാരണമായതിനുശേഷവും ഈ സമ്പ്രദായം നിലനിന്നു. ചിഹ്നത്തിന്റെ മുകളില് ഒരു വരയിട്ട് 1,000 ത്തിന്റെ പെരുക്കത്തെ സൂചിപ്പിക്കുന്ന സമ്പ്രദായം മധ്യകാലത്തു പ്രചാരത്തിലിരുന്നു. ഈ രീതി റോമില് ഉണ്ടായിരുന്നില്ല. കുറച്ചെഴുതുന്ന സമ്പ്രദായം ഹീബ്രുവിലും ചില റോമന് അക്കങ്ങളിലുമുണ്ട്. IV, IX എന്നിവ ഉദാഹരണങ്ങളാണ്. ഗുണിച്ചെഴുതി ഗ്രൂപ്പു ചെയ്യുന്ന സമ്പ്രദായം ചൈനയിലുണ്ടായിരുന്നു. സ്ഥാനമനുസരിച്ചുള്ള എഴുത്താണ് ആധുനിക ചൈനയില് നിലവിലുള്ളത്. പൂജ്യത്തെ o എന്ന വൃത്തചിഹ്നംകൊണ്ടാണ് സൂചിപ്പിക്കുന്നത്.
സൈഫറിംഗ് (Ciphering) പദ്ധതി. പാപ്പിറസിനെ (pappyrus)ക്കുറിച്ച് പ്രതിപാദിക്കുന്ന ഈജിപ്ഷ്യന് ഗണിത രേഖകളില്നിന്ന് ഗ്രഹിക്കാവുന്നതാണ് ഹെറാറ്റിക് അക്കങ്ങള്. സൈഫറിംഗ് അക്കപദ്ധതിയിലെ ഏറ്റവും പഴക്കമുള്ളത് ഹെറാറ്റിക് അക്കങ്ങളാണ്: 1, 2, ..., 9; X , 2 X, ...., 9X; C, 2C, ...., 9 C; M, 2M ...., 9M. പിന്നീട് നിലനിന്നിരുന്ന ഡിമോടിക് അക്കങ്ങള് ഇതിന്റെ വകഭേദമാണ്.
ബി.സി. 3-ാം ശ.-ത്തില് ഗ്രീസില് മറ്റൊരു രീതിയും നിലനിന്നിരുന്നു. ആദ്യക്ഷരങ്ങള് ഉപയോഗിച്ചുകൊണ്ടുള്ള സംഖ്യാസമ്പ്രദായത്തോട് ഇതിന് സാമ്യമുണ്ട്. ഇതും സൈഫറിംഗ് പദ്ധതിതന്നെ. അക്ഷരമാലയില് നിന്ന്, 1 മുതല് 9 വരെയുള്ള അക്കങ്ങള്ക്കും 10, 20, ...., 90; 100, 200, ...., 900, .... എന്നിവയ്ക്കും ക്രമത്തില് അക്ഷരങ്ങള് ഉപയോഗിക്കുന്നു. 24 അക്ഷരങ്ങള്
മാത്രമുള്ള ഗ്രീക് അക്ഷരമാല മതിയാകാതെ വന്നു. ഫിനീഷ്യന് ഭാഷയില്നിന്ന് F (വോ), യ (കോഫ്), S (സാമ്പി) എന്നിവയ്ക്കു സാമ്യമുള്ള അക്ഷരങ്ങള് അവര് സ്വീകരിച്ചു.
സ്ഥാനക്രമമനുസരിച്ചുള്ള സമ്പ്രദായമാണ് ഏറ്റവും ആധുനികം. എത്ര വലിയ സംഖ്യയായാലും എഴുതിക്കാണിക്കാന് ഏറ്റവും എളുപ്പമാര്ഗം ഇതാണ്. ഏതെങ്കിലുമൊരു അക്കം ആധാരമായെടുക്കാം. N=bn an + bn-1 an-1 + .. + b1 a + b0.5623 =5M6C2X3എന്ന പഴയ സമ്പ്രദായം ക്ളേശകരമാണ്. Nന്റെ വിവരണവ്യഞ്ജകത്തില് ഏതെങ്കിലും പദം ഇല്ലെങ്കില് ആ സ്ഥാനം
കുറിക്കാന് ഏതെങ്കിലുമൊരു ചിഹ്നം ആവശ്യമായി വന്നു. അല്ലെങ്കില് 356-ഉം 3056-ഉം ഒരുപോലെയിരിക്കും. ബി.സി. 3000-ത്തിനും 2000-ത്തിനുമിടയ്ക്ക് 60 ആധാരമാക്കി ഒരു സ്ഥാനക്രമസമ്പ്രദായമുണ്ടായി. 1 മുതല് 59 വരെയുള്ള അക്കങ്ങള്ക്കു പേരുകള് കണ്ടെത്തുക പ്രയാസമായി ഈ സമ്പ്രദായത്തില്
2,56,058 = (60)3 + 11 (60)2 + 47 (60) + 38 = 
മയന് സമ്പ്രദായം. കാലനിര്ണയം ചെയ്യാന് കഴിയാത്ത ഒരു പ്രാചീന കാലഘട്ടത്തില് തന്നെ സ്ഥാനക്രമമനുസരിച്ചുള്ള ഒരു അക്കസമ്പ്രദായം അമേരിക്കയിലെ മയന്കാര്ക്കുണ്ടായിരുന്നതായി കാണുന്നു. 20 ആധാരമാക്കിക്കൊണ്ടുള്ള ഈ സമ്പ്രദായത്തില് 1 മുതല് 19 വരെയുള്ളവയ്ക്ക് 5-ന്റെ ചിഹ്നത്തോടു ഗ്രൂപ്പു ചെയ്തുകൊണ്ടുള്ള ചിഹ്നങ്ങളാണ് ഉപയോഗിച്ചിരുന്നത്.
ഇന്ത്യന് സമ്പ്രദായം. വളരെ പ്രാചീനകാലം മുതല് ഇന്ത്യയില് സംഖ്യകളുടെ ആധാരമായി 'പത്ത്' സ്വീകരിച്ചിരുന്നു. പത്ത് ഒഴിച്ച് മറ്റൊരു ആധാരം (Base) വ്യാപകമായി ഉപയോഗിച്ചിരുന്നതിന്റെ പരാമര്ശം സംസ്കൃത സാഹിത്യം ആകെ പരിശോധിച്ചാലും കാണുകയില്ല. വളരെ ഉയര്ന്ന സംഖ്യകള്ക്ക് പേരുകളും ഇന്ത്യയില് നിലവിലുണ്ടായിരുന്നു. പതിനായിര (104) ത്തില് കവിഞ്ഞ സംഖ്യകളുടെ പേരുകള് ഗ്രീക്കുകാര്ക്കുണ്ടായിരുന്നില്ല. റോമാക്കാര്ക്ക് ആയിര(103)ത്തില് കവിഞ്ഞ ഒരു സംഖ്യക്കും പേരുണ്ടായിരുന്നില്ല. ഇന്ത്യയിലാകട്ടെ പതിനെട്ടു സ്ഥാനങ്ങളില് കവിഞ്ഞ സംഖ്യകള്ക്കു വരെ പ്രത്യേകം പേരുകള് ഉണ്ടായിരുന്നു.
യജൂര്വേദസംഹിതയില് (xvii-2) താഴെക്കാണുന്ന പേരുകള് അക്കങ്ങള്ക്കുപയോഗിച്ചിരുന്നു: ഏകം (1), ദശം (10), ശതം (100), സഹസ്രം (1,000), അയുതം (10,000), നിയുതം (1,00,000), പ്രയുതം (10,00,000), അര്ബുദം (1,00,00,000), നയാര്ബുദം (10,00,00,000), സമുദ്രം (1,00,00,00,000), മധ്യം (10,00,00,00,000), അന്തം (1,00,00,00,00,000), പരാര്ധം (10,00,00,00,00,000). തൈത്തിരീയസംഹിതയിലും (iv. 40. 11.4;vii. 2. 20. 1) ഇതേ പേരുകള് ഉപയോഗിച്ചിട്ടുണ്ട്. ചില്ലറ വ്യതിയാനങ്ങളോടെ ഈ പട്ടിക മൈത്രായനിയിലും (ii,8,14.) കാഠകസംഹിതയിലും(xvii-10) ഉപയോഗിച്ചിരുന്നതായി കാണാം. ബി.സി. 5-ാം ശ.-ത്തിലെ ബൌദ്ധകൃതിയായ ലളിതവിസ്താരത്തില് രാജേന്ദ്രലാല് മിത്ര, കോടിയില് കവിഞ്ഞ സംഖ്യകളുടെ പേരുകള് പരാമര്ശിക്കുന്നുണ്ട്.
ജൈനന്മാരുടെ മൗലികകൃതിയായ അനുയോഗദ്വാരസൂത്രത്തില് (ബി.സി. 100) ലോകജനസംഖ്യ തിട്ടപ്പെടുത്തുമ്പോള് 194 ദശസ്ഥാനങ്ങള് ഉള്ള ഒരു സംഖ്യയാണതെന്നു പറയുന്നു. ആര്യഭടന് 1 (499), ശ്രീധരാചാര്യന് (750), മഹാവീരന് (850), ഭാസ്കരാചാര്യന് II (1150), നാരായണാചാര്യന് (1356) എന്നീ ഭാരതീയ ഗണിതാചാര്യന്മാരെല്ലാം ദശസ്ഥാനങ്ങള് ഉപയോഗിച്ചിരുന്നു.
ഒന്നുമുതല് പത്തൊമ്പതുവരെ സ്ഥാനമുള്ള സംഖ്യകള്ക്ക് ഭാസ്കരാചാര്യന് ലീലാവതിയില് നാമനിര്ദേശം ചെയ്തിട്ടുണ്ട്.
'ഏക, ദശ, ശത, സഹസ്റാ,-
യുത, ലക്ഷ, പ്രയുത, കോടയഃ ക്രമശഃ
അര്ബുദ, മബ്ജം, ഖര്വ,-
നിഖര്വ, മഹാപദ്മ, ശങ്കവസ്തസ്മാത്
ജലധി, ശ്ചാന്ത്യം, മധ്യം,
പരാര്ധ, മിതി ദശഗുണോത്തരാഃ, സംജ്ഞാഃ
സംഖ്യായാഃ സ്ഥാനാനാം
വ്യവഹാരാര്ഥം കൃതാഃ പൂര്വൈഃ'
ഭാരതീയ ഗണിതശാസ്ത്രപ്രകാരം ഇങ്ങനെ പേരു നല്കപ്പെട്ടിട്ടുള്ള സംഖ്യകളെല്ലാം തന്നെ പത്തിന്റെ (10) അനുക്രമമായ ഘാത(ഗുണിത)ങ്ങളാണെന്ന് പ്രത്യേകം ഓര്മിക്കേണ്ടതുണ്ട്. മേലെഴുതിയ പേരുകള് സൂചിപ്പിക്കുന്ന സംഖ്യകളുടെ പട്ടിക താഴെ കൊടുക്കുന്നു:
1 ഏകം
10 ദശം
100 ശതം
1,000 സഹസ്രം
10,000 അയുതം
1,00,000 ലക്ഷം
10,00,000 പ്രയുതം
1,00,00,000 കോടി
10,00,00,000 അര്ബുദം
1,00,00,00,000 അബ്ജം
10,00,00,00,000 ഖര്വം
1,00,00,00,00,000 നിഖര്വം
10,00,00,00,00,000 മഹാപദ്മം
1,00,00,00,00,00,000 ശങ്കു
10,00,00,00,00,00,000 ജലധി (സമുദ്രം)
1,00,00,00,00,00,00,000 അന്ത്യം
10,00,00,00,00,00,00,000 മധ്യം
1,00,00,00,00,00,00,00,000 പരാര്ധം
10,00,00,00,00,00,00,00,000 ദശപരാര്ധം
സങ്കല്പാതീതമെന്ന് പറയാവുന്നതും സാമാന്യരീതിയില് എണ്ണിത്തീര്ക്കാന് ദുഷ്കരമായതും ആയ മഹാസംഖ്യകള്ക്ക് മലയാളത്തില് 'വെള്ളം' എന്നു പറഞ്ഞുവരുന്ന പതിവുണ്ടായിരുന്നു. ഭാസ്കരാചാര്യന്റെ ലീലാവതിയിലെ 'ജലധി'യില് (സമുദ്രം) നിന്നാകാം ഈ വിവര്ത്തിത സംജ്ഞ മലയാളത്തിന് കിട്ടിയത്. 'വെള്ളം പട' എന്നത് ഒരു വലിയ സംഖ്യക്കു പകരം മലയാളത്തില് ഇപ്പോഴും പറഞ്ഞുവരുന്ന പേരാണ്. പരമ്പരാഗതമായ ഈ വ്യവഹാരരീതി താഴെ കൊടുക്കുന്നു:
പാശ്ചാത്യ ഗണനപദ്ധതി അനുസരിച്ച് പ്രത്യേക സംജ്ഞ നല്കപ്പെട്ടിട്ടുള്ള ഏറ്റവും വലിയ സംഖ്യ 'ബില്യണ്' (billion) ആണ്. ഇതിലടങ്ങിയിരിക്കുന്ന സ്ഥാന(അക്ക)ങ്ങളെ സംബന്ധിച്ച് യു.എസിലും ഫ്രാന്സിലും ഒരു രീതിയും (1,00,00,00,000) ബ്രിട്ടനിലും ജര്മനിയിലും മറ്റൊരു രീതിയും (10,00,00,00,00,000) ആണ് പ്രചാരത്തിലിരിക്കുന്നത്. ഇപ്പോള് യു.എസ്. രീതി ഏതാണ്ട് സര്വസമ്മതമായി അംഗീകരിക്കപ്പെട്ടിരിക്കുന്നു. അതായത് 1 ബില്യണ് = 109 ആയിരം ബില്യണ് സമം ഒരു ട്രില്യണ് (Trillion). ഒരു ട്രില്യണ് = 1012.
പ്രാചീന അക്കങ്ങള്. മോഹഞ്ജൊദാരോയില് (ബി.സി. 5000) നിന്നു കണ്ടെടുത്ത പുരാരേഖകള് മുഴുവന് മനസിലാക്കാന് കഴിഞ്ഞിട്ടില്ല. എങ്കിലും കുത്തനെ ചെറുവരകള് നിരത്തിയോ ഒന്നിനു താഴെ മറ്റൊന്ന് എന്ന രൂപത്തിലോ അക്കങ്ങള് എഴുതിയിരുന്നു.
മോഹഞ്ജൊദാരോ ലിഖിതങ്ങള്ക്കും അശോകലിഖിതങ്ങള്ക്കും ഇടയില് 2700 വര്ഷത്തോളം അക്കങ്ങള് എങ്ങനെ ഉപയോഗിച്ചിരുന്നുവെന്നതിനെക്കുറിച്ച് അറിവൊന്നും ലഭ്യമല്ല. ഋഗ്വേദത്തില് എട്ടിനെക്കുറിച്ചും യജൂര്വേദത്തില് 1012 നോളം വലിയ സംഖ്യകളെക്കുറിച്ചുമുള്ള പരാമര്ശങ്ങള് വച്ചുനോക്കുമ്പോള് വളരെ വികാസം സിദ്ധിച്ച അക്കസമ്പ്രദായം ഇന്ത്യയില് നിലവിലിരുന്നുവെന്ന് ഊഹിക്കാന് കഴിയും. അശോകലിഖിതങ്ങളില് നിന്നും ഇന്ത്യയിലെ ഈ പ്രാചീനവികാസം ഗ്രഹിക്കാം. ആ ലിഖിതങ്ങള് ബ്രാഹ്മി, ഖരോഷ്ടി എന്നീ രണ്ടുതരം ലിപികളിലാണ് എഴുതിക്കാണുന്നത്.
(i) ബ്രാഹ്മി അക്കങ്ങള്. ഇന്ത്യയില് എല്ലായിടത്തും പ്രചാരത്തിലിരുന്ന ഒരുതരം ലിപിയാണ് ബ്രാഹ്മി. ഇത് ഇന്ത്യയുടെ ദേശീയ ലിപിയായിരുന്നു. ബി.സി. 1000-ത്തിനു മുമ്പുതന്നെ ഈ ലിപി പരിഷ്കരിച്ച നിലയിലെത്തിയിരുന്നു. ബ്രാഹ്മി അക്കങ്ങള് ഇന്ത്യയില് കണ്ടുപിടിച്ചവയാണ്. ഈ സമ്പ്രദായവും വിദേശീയമാണെന്നുവരുത്താന് ചില ശ്രമങ്ങള് നടന്നിട്ടുണ്ട്. പക്ഷേ പ്രസിദ്ധ ചരിത്രകാരനായ ലാങ്ഡണിന്റെ (Langdon's Mohenjodaro and the Indus Vally Civilization,Ch,xxiii) അഭിപ്രായത്തില് ബ്രാഹ്മി അക്കങ്ങള് ഇന്ത്യയില് തന്നെയാണ് കണ്ടുപിടിക്കപ്പെട്ടത്. ബ്രാഹ്മി അക്കങ്ങള് അശോക ലിഖിതങ്ങളില് (ബി.സി. 300) നിന്നാണ് മനസിലാക്കുന്നത്. ഉദാ.
മധ്യേന്ത്യയിലെ നാനാഘട്ട് കുന്നിന് മുകളിലുള്ള (പൂണൈയില് നിന്നു 120 കി.മീ. ദൂരെ) ഒരു ഗുഹയില് അക്കങ്ങള് കൊത്തിയ ലിഖിതങ്ങള് കണ്ടെത്തിയിട്ടുണ്ട്. ചില അക്കങ്ങള് താഴെ ചേര്ക്കുന്നു. (Journal of Bombay Branch of the Royal Aslatic Society , 1876, Vol,XII.P.404)
എ.ഡി. ഒന്നോ രണ്ടോ ശ.-ത്തിലേതായി മഹാരാഷ്ട്രയിലെ നാസിക് ജില്ലയിലെ ഗുഹകളില് കണ്ടെത്തിയ ലിഖിതങ്ങളിലും അക്കങ്ങള് രേഖപ്പെടുത്തിയിരിക്കുന്നതു കാണാം. (The inscription in the caves at nasik,EI Vol VII,P.47-74).
പൂജ്യത്തിന്റെ കണ്ടുപിടിത്തത്തോടെ സ്ഥാനക്രമം അനുസരിക്കുന്ന അക്കസമ്പ്രദായവും പൂജ്യവും ഇന്ത്യയിലെന്നപോലെ മറ്റു രാജ്യങ്ങളിലും സ്വീകരിച്ചുകാണുന്നു. പൂജ്യത്തിന്റെയും സ്ഥാനക്രമസമ്പ്രദായത്തിന്റെയും കണ്ടുപിടിത്തം ഇന്ത്യയിലാണെന്നതിന് ഏറ്റവും വലിയ തെളിവും ഇതുതന്നെ.
-, --, =,, എന്നിങ്ങനെ ഒന്ന്, രണ്ട്, മൂന്ന് എന്നിവ എഴുതുന്നതുകൊണ്ടുതന്നെ ബ്രാഹ്മി സമ്പ്രദായങ്ങളില് നിന്നും ഇതു വ്യത്യസ്തമാണ്. ഖരോഷ്ടിയിലും സെമിറ്റിക്കിലും I, II, III എന്നിങ്ങനെയാണ് എഴുതുന്നത്. 1, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, ........., 1000, 2000, ........ എന്നിവയ്ക്കെല്ലാം വ്യത്യസ്തമായ പ്രതീകങ്ങള് ബ്രാഹ്മി അക്കസമ്പ്രദായത്തിലുണ്ട്. എന്നാല് പഴയ ഖരോഷ്ടി അക്കസമ്പ്രദായത്തിലും ആദ്യകാല സെമിറ്റിക് രേഖകളിലും ഹൈറോഗ്ളിഫിക്സ് - ഫിനീഷ്യന് സമ്പ്രദായങ്ങളിലും 1, 10, 20, 100 എന്നിവയ്ക്കു മാത്രമേ പ്രതീകങ്ങളുള്ളു. ചിത്രമെഴുത്തില് നിന്നാണ് ഇന്ത്യയിലെ ബ്രാഹ്മി അക്കസമ്പ്രദായം രൂപപ്പെട്ടത് എന്നാണ് പല (Cunningham) ഇംഗ്ളീഷു ചരിത്രകാരന്മാരുടെയും അഭിപ്രായം.
(ii) ഖരോഷ്ടി അക്കങ്ങള്. വലത്തുനിന്ന് ഇടത്തോട്ട് എഴുതുന്ന ഒരു ലിപി സമ്പ്രദായമാണ് ഖരോഷ്ടി. കിഴക്കന് അഫ്ഗാനിസ്താനിലും വടക്കെ പഞ്ചാബിലും (ഗാന്ധാരം) പ്രധാനമായി കണ്ടെത്തിയ ലിഖിതങ്ങള് ഖരോഷ്ടി ലിപിയിലുള്ളതാണ്. ബി.സി. നാലും മൂന്നും ശ.-ങ്ങളിലാണ് ഇതു പ്രചാരത്തിലിരുന്നത്. അശോകന്റെ ലിഖിതങ്ങളില്നിന്നു കണ്ടെത്തിയ ഖരോഷ്ടി ലിപിയില് നാല് അക്കങ്ങളേ ഉള്ളൂ:
ശാകന്മാരുടെയും പാര്ത്തിയന്മാരുടെയും കുശാനന്മാരുടെയും ലിഖിതങ്ങളില്നിന്നും എ.ഡി. ഒന്നും രണ്ടും ശ.-ങ്ങളിലെ കുറേക്കൂടി പരിഷ്കരിച്ച ഖരോഷ്ടി അക്കങ്ങള് കണ്ടെത്തിയിട്ടുണ്ട്.
(iii) കടപയാദി സമ്പ്രദായം. അക്ഷരങ്ങള് അക്കങ്ങളായി ഉപയോഗിക്കുന്ന രീതിയും ഇന്ത്യയില് ഉണ്ടായിരുന്നു. സംസ്കൃത ഭാഷയിലെ വ്യഞ്ജനങ്ങളും (ഒന്നു മുതല് ഒമ്പതുവരെയുള്ള അക്കങ്ങള്ക്ക്) പൂജ്യവും ഉപയോഗിക്കുന്ന അക്ഷരസമ്പ്രദായമാണ് ഇത്. അക്കങ്ങള് രേഖപ്പെടുത്തുന്നതോടൊപ്പം അര്ഥം സ്ഫുരിക്കുന്ന വിധത്തില് വ്യഞ്ജനങ്ങള് ചേര്ത്ത് പ്രയോഗിച്ച് കാവ്യാത്മകമായ രീതിയില് അവ സംവിധാനം ചെയ്യാന് പല എഴുത്തുകാര്ക്കും കഴിഞ്ഞിരുന്നു. ആര്യഭടന് I (എ.ഡി. 499) ഈ കലയില് അദ്വിതീയനായിരുന്നു. ഈ സമ്പ്രദായമനുസരിച്ചുള്ള പട്ടിക താഴെ കാണാം.
ഈ പട്ടികയില് (ആദ്യത്തെ വരി) ഒന്നിനെ പ്രതിനിധാനം ചെയ്യുന്നത് കടപയ ആയതിനാല് കടപയാദി എന്ന് ഈ സമ്പ്രദായത്തിന് പേരുണ്ടായി.
എ.ഡി. 6-ാം ശ.-ത്തിലാണ് ഈ സമ്പ്രദായം ഉണ്ടായത്. ഇത് കാണുന്ന ആദ്യത്തെ രേഖ, ഭാസ്കരാചാര്യന് I-ന്റെ (522) ലഘുഭാസ്കരീയം എന്ന ഗ്രന്ഥമാണ്. ആര്യഭടന് II (950) ഈ സമ്പ്രദായം പരിഷ്കരിച്ച് ഉപയോഗിച്ചിരുന്നു. ആദ്യത്തെ രീതിയില് സ്വരങ്ങള് സ്വതന്ത്രമായി നില്ക്കുമ്പോള് പൂജ്യത്തെ പ്രതിനിധാനം ചെയ്യുന്നില്ല. ഇതില് സ്വരങ്ങള്ക്ക് പ്രത്യേകിച്ച് അക്കങ്ങളുമായി ബന്ധമില്ല. മുമ്പുണ്ടായിരുന്ന സമ്പ്രദായത്തില് നിന്നും ഇതിന്റെ വ്യത്യാസം, കൂട്ടക്ഷരങ്ങളില് ഉള്പ്പെടുന്ന വ്യഞ്ജനങ്ങള് സ്ഥാനഭേദമനുസിച്ച് പ്രത്യേകം അക്കങ്ങളെ സൂചിപ്പിക്കുന്നു എന്നതാണ്. ഇടത്തുനിന്നു വലത്തോട്ട് എന്ന എഴുത്തുരീതിയാണിതില്. "ധജഹേ കുനഹേത് സഭാ എന്നത് ആദ്യസമ്പ്രദായത്തില് 47801884-ഉം രണ്ടാമത്തേതില് 48810874-ഉം ആണ് സൂചിപ്പിക്കുന്നത്.
പാലി അക്ഷരമാലയില് ശ, ഷ എന്നിവയില്ലാത്തതിനാല് സ = 5, ഹ = 6, ഞ (?) = 7 തന്നെയാണ്. ബര്മയിലെ (മ്യാന്മര്) പാലി ഹസ്തലിഖിതങ്ങളില് പരിഷ്കരിച്ച ഈ കടപയാദി സമ്പ്രദായം ഉപയോഗിച്ചിരുന്നു.
നാലാമത്തെ ഭേദഗതിയാണ് 'കേരളസമ്പ്രദായ'മെന്നു പ്രസിദ്ധമായത്. ഇതും ആദ്യത്തെ സമ്പ്രദായം തന്നെയാണ്. ഇതില് വലത്ത്-ഇടത്ത് എന്ന എഴുത്തുക്രമം മാറ്റി ഇടത്ത്-വലത്ത് എന്ന ക്രമം സ്വീകരിച്ചിരിക്കുന്നു.
കേരളം, ആന്ധ്ര, സിലോണ്, ബര്മ, സയാം (തായ്ലന്ഡ്), ശ്രീലങ്ക എന്നിവിടങ്ങളില് പ്രയോഗത്തിലിരുന്ന മറ്റുചില അക്ഷര സമ്പ്രദായങ്ങളുമുണ്ട്. സംസ്കൃതഭാഷയിലെ 16 സ്വരങ്ങളും 34 വ്യഞ്ജനങ്ങളും പ്രയോജനപ്പെടുത്തുന്ന രീതിയാണ് അതില്. വ്യഞ്ജനങ്ങള് ക്രമത്തില് 1 മുതല് 34 സംഖ്യകളെയും അവ തന്നെ 'ആ' കാരാന്ത്യമായി പ്രയോഗിച്ചാല് 35 മുതല് 68 വരെയും അങ്ങനെ തുടര്ന്നും പ്രയോഗിക്കാറുണ്ട്. ക, കാ, ..... എന്നു തുടങ്ങിയ 16 അക്ഷരങ്ങള് 1 മുതല് 16 സംഖ്യകളെയും ഖ, ഖാ, ...... എന്നീ പതിനാറെണ്ണം, പതിനേഴു മുതല് മുപ്പത്തിനാലുവരെയും അങ്ങനെ തുടര്ന്നുള്ളവയും പ്രയോഗിച്ചിരുന്ന മറ്റൊരു അക്ഷരസമ്പ്രദായവും ഉണ്ടായിരുന്നു. ഇത് ശ്രീലങ്കയിലെ പാലി ഹസ്തലിഖിതങ്ങളിലാണ് കണ്ടെത്തിയിട്ടുള്ളത്. പന്ത്രണ്ട് സ്വരങ്ങളും 34 വ്യഞ്ജനങ്ങളും ഉപയോഗിച്ചുകൊണ്ടുള്ള മറ്റൊരു സമ്പ്രദായവുമുണ്ട്, പാലി കയ്യെഴുത്തു പ്രതികളില്. ഇതില് ക, കാ, .... എന്നിങ്ങനെ 13 മുതല് 26 വരെയും തുടര്ന്നും കാണാം. എ.ഡി. 3-ാം ശ.-ത്തിനു മുമ്പുവരെയെങ്കിലും ഈ അക്ഷരസമ്പ്രദായം വടക്കെ ഇന്ത്യയില് ഉപയോഗിച്ചു കണ്ടിട്ടില്ല.
അക്ഷരപല്ലി. പഴയ ഹസ്തലിഖിതങ്ങളില് അക്കങ്ങള്ക്ക് ഉപയോഗിച്ചുകാണുന്ന ശബ്ദങ്ങളുടെ പട്ടിക:
16-ാം ശ. വരെ ജൈനരുടെ ഹസ്തലിഖിതങ്ങളില് അക്ഷരപല്ലി ഉപയോഗിച്ചിരുന്നു. അതിനുശേഷം ദശാംശ-അക്കങ്ങള് പ്രയോഗിച്ചു. അക്ഷരപല്ലിയോട് സാദൃശ്യമുള്ള ഒരു സമ്പ്രദായം കേരളത്തില് നിലനിന്നിരുന്നു:
1 = ന, 2 = ന്ന, 3 = ന്യ, 4 = ഷ്ക്ര, 5 = ന്ധ്ര, 6 = ഹാ (ഹ), 7 = ഗ്ര, 8 = പ്ര, 9 = ദ്രെ (?), 10 = മ, 20 = ഥ, 30 = ല, 40 = പ്ത, 50 = ബ, 60 = ത്ര, 70 = രു (ത്രു), 80 = ച, 90 = ണ, 100 = ഞ
നോ: അങ്കപല്ലി, അക്ഷരപല്ലി
പൂജ്യമെന്ന ആശയം. മയന്കാരും ബാബിലോണിയക്കാരും ഗണിതസൗകര്യമുള്ള തരത്തിലല്ല അക്കങ്ങള് അംഗീകരിച്ചത്. യഥാക്രമം 20-ഉം 60-ഉം വരെയുള്ള അക്കങ്ങള്ക്ക് ഒറ്റചിഹ്നങ്ങള് അവര്ക്കുണ്ടായിരുന്നില്ലെന്നതാണ് അതിനു കാരണം. ഇന്ത്യയിലാണ് ഈ വഴിക്കുള്ള പുരോഗതിയുണ്ടായത്. ഇന്നു പാശ്ചാത്യ രാജ്യങ്ങളില് ഉപയോഗത്തിലിരിക്കുന്നവിധം പൂജ്യം ആദ്യം പ്രയോഗിച്ചതും ഇന്ത്യക്കാര് തന്നെയാണ്. ഏകദേശം എ.ഡി. 1-ാം ശ.-ത്തില് ഗുജറാത്തിലാണ് പൂജ്യത്തിന് ഒരു പ്രതീകം കണ്ടെത്തിയതെന്നതിന് ചില രേഖകളുണ്ട്. 'ശൂന്യ'മെന്ന് വ്യവഹരിക്കപ്പെടുന്ന പൂജ്യത്തിന് ചിഹ്നമായി ബിന്ദു ആണോ വൃത്തം ആണോ ആദ്യം ഉപയോഗിച്ചതെന്ന് വ്യക്തമല്ല. എ.ഡി. 800-ല് അറബികള് 'സിഫര്' എന്നും പിന്നീട് 'സൈഫര്' എന്നും പേരിട്ട് അതു പകര്ത്തി. 1200-ലാണ് അത് ലത്തീനില് എത്തിയത്. പൂജ്യത്തിന്റെ കണ്ടുപിടിത്തം ഗണിതത്തിലെ ഒരു നിര്ണായക സംഭവമാണ്.
(i) പൂജ്യം ഇന്ത്യയില്. ബി.സി. 200-നു മുമ്പുതന്നെ പിംഗളന് എന്ന ഗണിതശാസ്ത്രജ്ഞന് ചാന്ദ്രസൂത്രം എന്ന ഗ്രന്ഥത്തില് പൂജ്യത്തിന് 0 എന്ന ചിഹ്നം അളവുകളില് ഉപയോഗിച്ചിരുന്നു. ബി.സി. 200-നു മുമ്പുതന്നെ ഇന്ത്യയില് ഈ ചിഹ്നം ഉണ്ടായിരുന്നു എന്നതിന് ഇതു തെളിവാണ്. ഏകദേശം ഇതേ കാലഘട്ടത്തിലെ ബക്ഷാലി ഹസ്തലിഖിതങ്ങളിലും പൂജ്യത്തിന് 0 എന്ന ചിഹ്നം ഉപയോഗിച്ചിട്ടുണ്ട്. പഞ്ചസിദ്ധാന്തിക (505) എന്ന ജ്യോതിശ്ശാസ്ത്രഗ്രന്ഥത്തില് (0) പൂജ്യത്തെ പല സന്ദര്ഭങ്ങളിലും പരാമര്ശിക്കുന്നുണ്ട്. വരാഹമിഹിരന്റെ സമകാലികനായിരുന്ന ജിനഭദ്രഗണിയുടെ (529-589) ഗ്രന്ഥങ്ങളില് പൂജ്യത്തിന്റെ ചിഹ്നം ഒരു അക്കമെന്ന നിലയില് കൈകാര്യം ചെയ്തു കാണുന്നു. ഭാസ്കരാചാര്യന് I (522) മഹാഭാസ്കരീയം എന്ന ഗ്രന്ഥത്തില് പൂജ്യത്തെ മറ്റു സംഖ്യകളില്നിന്ന് കുറയ്ക്കുന്ന സമ്പ്രദായം വിവരിക്കുന്നുണ്ട്. പൂജ്യചിഹ്നം ഉപയോഗിച്ച് ആര്യഭടീയത്തില് അക്കങ്ങളുടെ സ്ഥാനക്രമസമ്പ്രദായം ഉപയോഗിച്ചു കാണാം. സിദ്ധസേനഗണി (6-ാം ശ.) പൂജ്യം ഉപയോഗിച്ചിരുന്നതായി ചില വ്യാഖ്യാനഗ്രന്ഥങ്ങളില് നിന്നു മനസിലാക്കാം. ഇന്ത്യയിലെ എല്ലാ ഗണിതശാസ്ത്ര ഗ്രന്ഥങ്ങളിലും പൂജ്യം കൊണ്ടുള്ള ഗണിതപ്രക്രിയകള് വിവരിച്ചിട്ടുണ്ട്. ഇവിടെയെല്ലാം ഏതെങ്കിലും ഒരു ചിഹ്നം പൂജ്യത്തിനുപയോഗിച്ചിട്ടുമുണ്ട്.
പൂജ്യത്തിന് ഉപയോഗിച്ചിരുന്ന ചിഹ്നം വിവിധ രൂപങ്ങളില് ആയിരുന്നു. ബക്ഷാലി കൈയെഴുത്തുപ്രതിയില് ഒരു ബിന്ദു ആണ് ഉപയോഗിച്ചിരുന്നത്. എ.ഡി. 3-ാം ശ.-ത്തിലെ ഈ രേഖയില് ബിന്ദുതന്നെയാണോ എന്ന് പിന്നീട് ലഭ്യമായിട്ടുള്ള (9-ാം ശ.-ത്തില്) പ്രതികളില്നിന്നുമാത്രം നിശ്ചയിക്കാവുന്നതല്ല. 6-ാം ശ.-ത്തിന്റെ അവസാനകാലത്ത് ജീവിച്ചിരുന്ന സുബന്ധു എന്ന ഗണിതശാസ്ത്രജ്ഞന്റെ വാസവദത്ത എന്ന ഗ്രന്ഥത്തില് നിന്ന് ബിന്ദു പൂജ്യത്തെ സൂചിപ്പിച്ചിരുന്നതായി മനസിലാക്കാം. ഒരു ബിന്ദു ഒരു സംഖ്യയെ പത്തിരട്ടിയാക്കുന്നതുപോലെ '....' എന്നു ഹിന്ദി കവി ബിഹാരിലാല് (1595-1663?) പ്രയോഗിച്ചിട്ടുണ്ട്.
8-ാം ശ.-ത്തിലെ ജയ്വര്ധന് II-ന്റെ രഘോളിത്തകിടുകള് (Ragholi Plates) ആണ് പൂജ്യത്തിന് ചെറിയ വൃത്തം (o) അക്കമായി ഉപയോഗിച്ചിരുന്നതിന്റെ, ലഭ്യമായ ഏറ്റവും പ്രാചീനരേഖ. ഭോജദേവന്റെ ഗ്വാളിയര് ലിഖിതങ്ങളില് ചെറുവൃത്തം പൂജ്യചിഹ്നമായി ഉപയോഗിച്ചു കാണുന്നു. 8-ാം ശ.-ത്തിനു മുമ്പു മുതല് ചെറുവൃത്തം പൂജ്യചിഹ്നമായി ഉപയോഗിച്ചിരുന്നുവെന്നു നിശ്ചയിക്കാം.
.... 0 0 0 0 0 ഇങ്ങനെ എഴുതി ഇടത്തുനിന്നു വലത്തോട്ട് ആദ്യത്തെ പൂജ്യം തൊട്ട് ഒന്ന്, പത്ത്, നൂറ്, ആയിരം, .... എന്നിങ്ങനെ സ്ഥാനക്രമം പറയുന്ന സമ്പ്രദായം ഭാസ്കരാചാര്യന് ക-ന്റെ കാലത്തും ഉണ്ടായിരുന്നു. അങ്കഗണിതത്തെ സംബന്ധിച്ച (പാടിഗണിതം) എല്ലാ ഗ്രന്ഥങ്ങളിലും അറിയാത്തതിനെ സൂചിപ്പിക്കുന്ന ചിഹ്നമായി 0 ഉപയോഗിച്ചിരുന്നു. എ.ഡി. 3-ാം ശ.-ത്തിലാണ് പൂജ്യത്തിന്റെ ഈ ഉപയോഗം കണ്ടെത്തിയത്. ബക്ഷാലി ഹസ്തലിഖിതത്തിലും ഇങ്ങനെ പൂജ്യം ഉപയോഗിച്ചിട്ടുണ്ട്. അക്കം ഇല്ല എന്നു സൂചിപ്പിക്കയാണ് 0 എന്ന ചിഹ്നം കൊണ്ടുദ്ദേശിച്ചിട്ടുള്ളത്.
(ii) പൂജ്യത്തിന്റെ ഗണിതം. പൂജ്യത്തിന്റെ എല്ലാ പ്രയോഗങ്ങളും ഇന്ത്യയില് ഉണ്ടായിരുന്നു. മറ്റു സംഖ്യകളോടൊപ്പം പൂജ്യത്തെയും ഇന്ത്യയില് അക്കം എന്ന നിലയില് അംഗീകരിച്ചിരുന്നു.
'പൂജ്യം', 'ശൂന്യം' (0) എന്ന് പറയുന്ന ചിഹ്നം സ്വയം നിന്നാല് ഒരു സംഖ്യയേയും സൂചിപ്പിക്കുന്നില്ല. എന്നാല് ഒരുപൂര്ണസംഖ്യയുടെ ഒടുവില് പൂജ്യം വന്നാല് അതിന്റെ മൂല്യത്തെ ഇത് പത്തുമടങ്ങ് വര്ധിപ്പിക്കുന്നു. അതുപോലെ, ദശാംശഭിന്നങ്ങളില് ഇടത്തെ അറ്റത്ത് വരുന്ന പൂജ്യം സംഖ്യാമൂല്യത്തെ പത്തിലൊന്നായി കുറയ്ക്കുകയും ചെയ്യുന്നു.
വരാഹമിഹിരന്റെ പഞ്ചസിദ്ധാന്തിക എന്ന ജ്യോതിഃശാസ്ത്രഗ്രന്ഥത്തില് പൂജ്യംകൊണ്ടുള്ള സങ്കലനവും വ്യവകലനവും സാന്ദര്ഭികമായി പ്രതിപാദിച്ചിട്ടുണ്ട്. ദശാംശഗണിതം മുഴുവനും ആര്യഭടീയവ്യാഖ്യാനത്തില് ഭാസ്കരാചാര്യന് 1 (522) ചേര്ത്തിരിക്കുന്നു. ബ്രഹ്മഗുപ്തന്റെ ഗ്രന്ഥത്തിലും (628) പിന്നീടുള്ള മറ്റു ഗണിത ഗ്രന്ഥങ്ങളിലും പൂജ്യം കൊണ്ടുള്ള ക്രിയകള് വിവരിച്ചുകാണാം. അങ്കഗണിതത്തിലും (Arithmetic) ബീജഗണിതത്തിലും (Algebra) വ്യത്യസ്ത രീതിയിലാണ് പൂജ്യം കൈകാര്യം ചെയ്തിരിക്കുന്നത്.
അങ്കഗണിതത്തില്, ഒരു സംഖ്യയില് നിന്ന് അതേ സംഖ്യകുറച്ചാല് കിട്ടുന്ന ഫലത്തെയാണ് പൂജ്യമെന്നു നിര്വചിച്ചിരിക്കുന്നത്. പൂജ്യംകൊണ്ട് സങ്കലനം, വ്യവകലനം, ഗുണനം എന്നിവ നടത്താമെന്നും ഹരണം നടത്തരുതെന്നും അങ്കഗണിതത്തില് നിര്ദേശിച്ചിട്ടുണ്ട്. ഒരു സംഖ്യയോട് പൂജ്യം കൂട്ടിയാല് ഫലം ആ സംഖ്യ തന്നെ; ഒരു സംഖ്യയില് നിന്നു പൂജ്യം കുറച്ചാലും ഫലം ആ സംഖ്യതന്നെ; ഒരു സംഖ്യയെ പൂജ്യം കൊണ്ടു ഗുണിച്ചാല് ഫലം പൂജ്യമാണ്. ശ്രീധരാചാര്യനും ആര്യഭടന് II-നും (മഹാസിദ്ധാന്താ) നാരായണാചാര്യനും (പാടിഗണിതം) മഹാവീരാചാര്യനും (ഗണിതസാരസംഗ്രഹം) ഇക്കാര്യങ്ങള് വിവരിക്കുന്നുണ്ട്. ഒരു സംഖ്യയെ പൂജ്യംകൊണ്ടു ഹരിച്ചാല് ഫലം ആ സംഖ്യതന്നെയെന്ന് മഹാവീരന് പ്രസ്താവിച്ചിരിക്കുന്നത് അബദ്ധമാണ്. എന്നാല് മഹാവീരനു രണ്ടു നൂറ്റാണ്ടുകള്ക്കു മുമ്പുതന്നെ ബ്രഹ്മഗുപ്തന് ശരിയായ ഉത്തരം അതിനു നല്കിയിരിക്കെ മഹാവീരന് ഈ തെറ്റു പറ്റിയത് വിചിത്രമായിരിക്കുന്നു.
ബ്രഹ്മസ്ഫുടസിദ്ധാന്തത്തിലാണ് (628) പൂജ്യത്തെ ബീജീയാങ്കമെന്ന നിലയില് ആദ്യമായി കൈകാര്യം ചെയ്തിരിക്കുന്നത്.
ഋണസംഖ്യയില് നിന്നു പൂജ്യം കുറച്ചാല് ഋണസംഖ്യ തന്നെ ഫലം; ധനസംഖ്യയില് നിന്നാണെങ്കില് ധനസംഖ്യയും; പൂജ്യത്തില്നിന്നാണെങ്കില് പൂജ്യവും. ഋണസംഖ്യയും പൂജ്യവും തമ്മിലോ ധനസംഖ്യയും പൂജ്യവും തമ്മിലോ ഗുണിച്ചാല് പൂജ്യമാണ് ഫലം; പൂജ്യങ്ങള് തമ്മിലായാലും പൂജ്യം തന്നെ.
ഭാസ്കരാചാര്യന് II ലീലാവതി എന്ന ഗ്രന്ഥത്തിലും ഇത്തരം നിഗമനങ്ങള് പൂജ്യത്തെക്കുറിച്ച് ചേര്ത്തിട്ടുണ്ട്. പൂജ്യം ഒരു അനന്തസൂക്ഷ്മമായി (Infinitesimal) ബ്രഹ്മഗുപ്താചാര്യന് ഉപയോഗിച്ചിട്ടുണ്ട്. x ÷ 0, 0 ÷ x എന്നിവ x/0, 0/x എന്നിങ്ങനെ എഴുതാം. ഭാസ്കരാചാര്യന് II ഈ അര്ഥത്തില് പൂജ്യത്തെ കലനത്തില് (Calculus) പ്രകടമായി പ്രയോഗിച്ചിട്ടുണ്ട്. x/0 = α(അനന്തം), α+ k = α എന്നീ ഫലഭാഗങ്ങളും അദ്ദേഹത്തിനു വശമായിരുന്നു. = 0 എന്ന് തെറ്റായി ബ്രഹ്മഗുപ്തന് പ്രസ്താവിച്ചിട്ടുള്ളത് ഭാസ്കരാചാര്യന് 11 സീമാസിദ്ധാന്തം (Limit theory) ഉപയോഗിച്ച് തിരുത്തിയിട്ടുണ്ട്.
ആധുനിക സമ്പ്രദായം. ആധുനിക അക്കസമ്പ്രദായത്തിന്റെ ഉറവിടം ഇന്ത്യയിലാണെന്ന് പറയാം. അറബിക് അക്കങ്ങളെന്നു പറയുന്നത് അത്ര ശരിയല്ല. ചരിത്രരേഖകള് വച്ചുനോക്കിയാല് 1, 4, 6 എന്നിവ അശോകന്റെ ശാസനങ്ങളിലും (ബി.സി. 3-ാം ശ.) 2, 4, 6, 7, 9 എന്നിവ നാനാഘട് ശാസനങ്ങളിലും (ബി.സി. 2-ാം ശ.) 2, 3, 4, 5, 6, 7, 9 നാസിക് ശാസനങ്ങളിലും (എ.ഡി. ഒന്നും രണ്ടും ശ.-ങ്ങള്) കാണാം. മെസപ്പൊട്ടേമിയയിലെ ഒരു മെത്രാനായിരുന്ന സെവേരസ് സെബോക്ടിന്റെ ഒരു രേഖയില് നിന്നാണ് 'ഹിന്ദുഅക്ക'ങ്ങളെക്കുറിച്ചുള്ള ആദ്യത്തെ പരാമര്ശം പാശ്ചാത്യര്ക്കു കിട്ടുന്നത്. എ.ഡി. 8-ാം ശ.-ത്തിന്റെ അവസാനത്തില് ചില ഭാരതീയ ജ്യോതിഃശാസ്ത്ര ഗ്രന്ഥങ്ങളുടെ പരാവര്ത്തനങ്ങള് അറേബ്യയില് ഉണ്ടായി. അറബി പണ്ഡിതന്മാര്ക്ക് ഇന്ത്യന് അക്കങ്ങള് പരിചിതമായിരുന്നു. എ.ഡി. 825-ല് അല്-ഖവാരിസ്മി ഇതേപ്പറ്റി ഒരു ബൃഹദ്ഗ്രന്ഥം തന്നെ അറബി ഭാഷയില് രചിച്ചിട്ടുണ്ട്. ഇതിന്റെ പരിഭാഷയും പാശ്ചാത്യര്ക്കു കിട്ടി. എ.ഡി. 976-ല് സ്പെയിന് ഭാഷയില് എഴുതിയ ഒരു ഗ്രന്ഥമാണ് ഇക്കാര്യത്തില് യൂറോപ്പുകാരുടെ പ്രമാണം. അറബിവഴിയല്ലാതെ തന്നെ യൂറോപ്പില് ഇന്ത്യന് അക്കങ്ങള് എത്തിയിരുന്നു.
പത്ത് ആധാരമാക്കിക്കൊണ്ടുള്ള അക്കസമ്പ്രദായം ഇന്ന് അന്താരാഷ്ട്ര ഗണിതഭാഷയായിത്തീര്ന്നിരിക്കുകയാണ്. എങ്കിലും ചൈനീസ്, ജപ്പാന്, റഷ്യന്, ഇംഗ്ളീഷ്, ജര്മന്, ഗ്രീക് എന്നീ ഭാഷകളില് പ്രചാരമുള്ളത് രണ്ട് ആധാരമാക്കിക്കൊണ്ടുള്ള പദ്ധതിയാണ് (ദ്വയാംഗ സമ്പ്രദായം). ഇലക്ട്രോണിക് കംപ്യൂട്ടറുകളില് പ്രയോഗിക്കുന്നതും ഈ പദ്ധതി തന്നെ. യാന്ത്രിക സ്വഭാവത്തിനനുയോജ്യമായി വിജ്ഞാനം 'പരാവര്ത്തനം' ചെയ്യുവാന് ഉതകുന്ന ഏറ്റവും എളുപ്പമുള്ള സമ്പ്രദായം ഈ ദ്വയാങ്കപദ്ധതിയാണ്. ഇതില് 0, 1 എന്നീ ചിഹ്നങ്ങള് മാത്രമേ ആവശ്യമുള്ളു. സംഖ്യകള് ഈ സമ്പ്രദായത്തില് രേഖപ്പെടുത്തുന്ന രീതി താഴെ ചേര്ക്കുന്നു.
നോ: അക്ഷരസംഖ്യ; അങ്കഗണിതം; കംപ്യൂട്ടര്; കലിസംഖ്യ; പരല്പേര്; സംഖ്യകള്