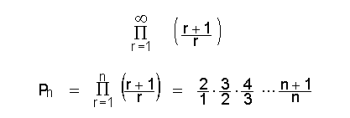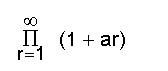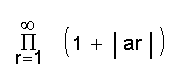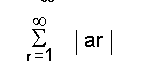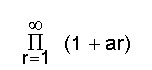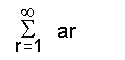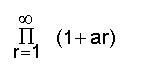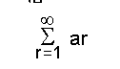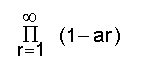This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
അനന്ത ഗുണിതങ്ങള്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→അനന്ത ഗുണിതങ്ങള്) |
|||
| വരി 7: | വരി 7: | ||
എന്നത് മുന് ഉദാഹരണത്തിലെ ആംശികഗുണിതം (partial product) എന്നു പറയപ്പെടുന്നു. (ഒരു അനന്തഗുണിതത്തിന്റെ) ആംശിക ഗുണിതത്തിലുള്ള ഘടകങ്ങളുടെ എണ്ണം വര്ധിച്ചുകൊണ്ടിരിക്കുമ്പോള്, അതിന്റെ മൂല്യങ്ങള് പൂജ്യത്തില്നിന്നു ഭിന്നമായ ഒരു പരിമിത സംഖ്യയോട് അടുത്തുകൊണ്ടിരിക്കുകയാണെങ്കില്, ആ അനന്തഗുണിതത്തെ അഭികേന്ദ്രസരണം (convergent) എന്നും; ആ ആംശികഗുണിതത്തിന്റെ മൂല്യങ്ങള് ഘടകങ്ങളുടെ എണ്ണം വര്ധിക്കുന്നതോടൊത്ത്, അനന്തതയെയോ പൂജ്യത്തെയോ സമീപിച്ചു കൊണ്ടിരിക്കുകയാണെങ്കില്,ആ അനന്തഗുണിതത്തെ അപകേന്ദ്രസരണം (divergent) എന്നും പറയുന്നു. അനന്തഗുണിതത്തിലെ ഏതെങ്കിലും ഒരു ഘടകത്തിന്റെ മൂല്യം പൂജ്യമാണെങ്കില് ആ അനന്തഗുണിതത്തിന്റെ തന്നെ മൂല്യം പൂജ്യമാണ്. ഒരു ആംശികഗുണിതത്തിന്റെ മൂല്യം പൂജ്യത്തെ സമീപിക്കുന്നു എന്നു പറയുമ്പോള് ഘടകങ്ങള്ക്കൊന്നിനും പൂജ്യം മൂല്യമായിരിക്കുകയില്ലെന്ന് ഓര്ക്കേണ്ടതുണ്ട്. പ്രതിപാദന സൌകര്യത്തെ ഉദ്ദേശിച്ച് അനന്തഗുണിതങ്ങളെ | എന്നത് മുന് ഉദാഹരണത്തിലെ ആംശികഗുണിതം (partial product) എന്നു പറയപ്പെടുന്നു. (ഒരു അനന്തഗുണിതത്തിന്റെ) ആംശിക ഗുണിതത്തിലുള്ള ഘടകങ്ങളുടെ എണ്ണം വര്ധിച്ചുകൊണ്ടിരിക്കുമ്പോള്, അതിന്റെ മൂല്യങ്ങള് പൂജ്യത്തില്നിന്നു ഭിന്നമായ ഒരു പരിമിത സംഖ്യയോട് അടുത്തുകൊണ്ടിരിക്കുകയാണെങ്കില്, ആ അനന്തഗുണിതത്തെ അഭികേന്ദ്രസരണം (convergent) എന്നും; ആ ആംശികഗുണിതത്തിന്റെ മൂല്യങ്ങള് ഘടകങ്ങളുടെ എണ്ണം വര്ധിക്കുന്നതോടൊത്ത്, അനന്തതയെയോ പൂജ്യത്തെയോ സമീപിച്ചു കൊണ്ടിരിക്കുകയാണെങ്കില്,ആ അനന്തഗുണിതത്തെ അപകേന്ദ്രസരണം (divergent) എന്നും പറയുന്നു. അനന്തഗുണിതത്തിലെ ഏതെങ്കിലും ഒരു ഘടകത്തിന്റെ മൂല്യം പൂജ്യമാണെങ്കില് ആ അനന്തഗുണിതത്തിന്റെ തന്നെ മൂല്യം പൂജ്യമാണ്. ഒരു ആംശികഗുണിതത്തിന്റെ മൂല്യം പൂജ്യത്തെ സമീപിക്കുന്നു എന്നു പറയുമ്പോള് ഘടകങ്ങള്ക്കൊന്നിനും പൂജ്യം മൂല്യമായിരിക്കുകയില്ലെന്ന് ഓര്ക്കേണ്ടതുണ്ട്. പ്രതിപാദന സൌകര്യത്തെ ഉദ്ദേശിച്ച് അനന്തഗുണിതങ്ങളെ | ||
| + | [[Image:466f.png]] | ||
എന്ന തരത്തിലാണ് എഴുതിപ്പോരുന്നത്. അപ്പോള് P_n എന്ന ആംശികഗുണിതം | എന്ന തരത്തിലാണ് എഴുതിപ്പോരുന്നത്. അപ്പോള് P_n എന്ന ആംശികഗുണിതം | ||
| + | [[Image:466f.png]] | ||
എന്നാകും. ഘടകങ്ങളെല്ലാം പൂജ്യത്തില്നിന്നു ഭിന്നമായിരിക്കുന്ന | എന്നാകും. ഘടകങ്ങളെല്ലാം പൂജ്യത്തില്നിന്നു ഭിന്നമായിരിക്കുന്ന | ||
| + | [[Image:466f.png]] | ||
എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമാകാമെങ്കില് അവശ്യം വേണ്ടതും (necessary) മതിയായതുമായ (sufficient) ഒരു വ്യവസ്ഥ ഇതാണ്: എന്ന ധനരാശി എത്ര ചെറുതായിരുന്നാലും, ിച0 ആണെങ്കില്, m = 1, 2, 3... എന്ന മൂല്യങ്ങള്ക്കെല്ലാം | എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമാകാമെങ്കില് അവശ്യം വേണ്ടതും (necessary) മതിയായതുമായ (sufficient) ഒരു വ്യവസ്ഥ ഇതാണ്: എന്ന ധനരാശി എത്ര ചെറുതായിരുന്നാലും, ിച0 ആണെങ്കില്, m = 1, 2, 3... എന്ന മൂല്യങ്ങള്ക്കെല്ലാം | ||
| + | [[Image:p466d.png]] | ||
എന്ന അസമത (inequality) ഒത്തുവരത്തക്കവണ്ണം N_0 എന്നൊരു പൂര്ണസംഖ്യ കണ്ടെത്തുവാന് കഴിയണം. ഈ പ്രസ്താവനയിലെ m-ന് 1 എന്ന മൂല്യം കല്പിക്കുന്നതായാല് | എന്ന അസമത (inequality) ഒത്തുവരത്തക്കവണ്ണം N_0 എന്നൊരു പൂര്ണസംഖ്യ കണ്ടെത്തുവാന് കഴിയണം. ഈ പ്രസ്താവനയിലെ m-ന് 1 എന്ന മൂല്യം കല്പിക്കുന്നതായാല് | ||
| + | [[Image:p466e.png]] | ||
| - | എന്ന അഭികേന്ദ്രസരണ-അനന്തഗുണിതത്തില് | + | എന്ന അഭികേന്ദ്രസരണ-അനന്തഗുണിതത്തില് a<sub>n+1</sub> പൂജ്യത്തെ സമീപിച്ചുകൊണ്ടിരിക്കുമെന്നു സിദ്ധിക്കുന്നു. ഈ നിബന്ധന അഭികേന്ദ്രസരണത്തിനു വേണ്ടതാണ്; പക്ഷേ മതിയാകുന്നതല്ല.അനന്തഗുണിതങ്ങളെ സംബന്ധിച്ചുള്ള ചില പ്രമേയങ്ങള് (theorems) ചുവടെ ചേര്ക്കുന്നു. ഇവിടെ എല്ലാ മൃ-ഉം വാസ്തവികസംഖ്യകള് (real numbers) ആണെന്നു സങ്കല്പിച്ചിരിക്കുകയാണ്. |
| - | + | ||
| - | + | ||
| + | '''പ്രമേയം-1'''. എല്ലാ ar-ഉം ധനാത്മകമാണെന്നിരിക്കട്ടെ. അപ്പോള് a<sub>1</sub> + a<sub>2</sub> + a<sub>3</sub> + ...എന്ന അനന്തശ്രേണി അഭികേന്ദ്രസരണമാണെങ്കില്, എങ്കില് മാത്രമേ | ||
| + | [[Image:p466c.png]] | ||
എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കൂ. | എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കൂ. | ||
| വരി 31: | വരി 36: | ||
'''പ്രമേയം-2.''' | '''പ്രമേയം-2.''' | ||
| - | + | [[Image:p466g.png]] | |
എന്ന അനന്തഗുണിതം അല്ലെങ്കില് | എന്ന അനന്തഗുണിതം അല്ലെങ്കില് | ||
| - | + | [[Image:p466h.png]] | |
എന്ന അനന്തശ്രേണി അഭികേന്ദ്രസരണമാണെങ്കില്, തീര്ച്ചയായും | എന്ന അനന്തശ്രേണി അഭികേന്ദ്രസരണമാണെങ്കില്, തീര്ച്ചയായും | ||
| + | [[Image:p466i.png]] | ||
എന്ന അനന്തഗുണിതവും അഭികേന്ദ്രസരണമായിരിക്കും. അഥവാ | എന്ന അനന്തഗുണിതവും അഭികേന്ദ്രസരണമായിരിക്കും. അഥവാ | ||
| + | |||
| + | [[Image:p466j.png]] | ||
എന്ന അനന്തശ്രേണി നിരപേക്ഷ അഭികേന്ദ്രസരണം (absolutely convergent) ആണെങ്കില്, എങ്കില് മാത്രമേ | എന്ന അനന്തശ്രേണി നിരപേക്ഷ അഭികേന്ദ്രസരണം (absolutely convergent) ആണെങ്കില്, എങ്കില് മാത്രമേ | ||
| + | |||
| + | [[Image:p466k.png]] | ||
| വരി 51: | വരി 61: | ||
എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കുകയുള്ളു. | എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കുകയുള്ളു. | ||
| - | '''പ്രമേയം-3'''. എല്ലാ ar-ഉം 0 ar < 1 എന്ന നിബന്ധന പാലിക്കുന്നുണ്ടെന്നിരിക്കട്ടെ. അപ്പോള് | + | '''പ്രമേയം-3'''. എല്ലാ ar-ഉം 0≤ ar < 1 എന്ന നിബന്ധന പാലിക്കുന്നുണ്ടെന്നിരിക്കട്ടെ. അപ്പോള് |
| + | |||
| + | [[Image:p466l.png]] | ||
അഭികേന്ദ്രസരണമാണെങ്കില്, എങ്കില് മാത്രമേ | അഭികേന്ദ്രസരണമാണെങ്കില്, എങ്കില് മാത്രമേ | ||
| + | |||
| + | [[Image:p466m.png]] | ||
07:49, 17 മാര്ച്ച് 2008-നു നിലവിലുണ്ടായിരുന്ന രൂപം
അനന്ത ഗുണിതങ്ങള്
Infinite products
ഗണിതത്തില് ഘടകങ്ങള് അവസാനമില്ലാതെ തുടര്ച്ചയായി ചേര്ത്ത് ഗുണിച്ചുണ്ടാകുന്ന ഫലം. ?എന്ന ചിഹ്നം ഉപയോഗിച്ച് അനന്തഗുണിതത്തെ സംക്ഷിപ്തരൂപത്തില് എഴുതാം. ഉദാ.2/1.3/2.4/3........... എന്ന അനന്തഗുണിതം തന്നെയാണ്:
എന്നത് മുന് ഉദാഹരണത്തിലെ ആംശികഗുണിതം (partial product) എന്നു പറയപ്പെടുന്നു. (ഒരു അനന്തഗുണിതത്തിന്റെ) ആംശിക ഗുണിതത്തിലുള്ള ഘടകങ്ങളുടെ എണ്ണം വര്ധിച്ചുകൊണ്ടിരിക്കുമ്പോള്, അതിന്റെ മൂല്യങ്ങള് പൂജ്യത്തില്നിന്നു ഭിന്നമായ ഒരു പരിമിത സംഖ്യയോട് അടുത്തുകൊണ്ടിരിക്കുകയാണെങ്കില്, ആ അനന്തഗുണിതത്തെ അഭികേന്ദ്രസരണം (convergent) എന്നും; ആ ആംശികഗുണിതത്തിന്റെ മൂല്യങ്ങള് ഘടകങ്ങളുടെ എണ്ണം വര്ധിക്കുന്നതോടൊത്ത്, അനന്തതയെയോ പൂജ്യത്തെയോ സമീപിച്ചു കൊണ്ടിരിക്കുകയാണെങ്കില്,ആ അനന്തഗുണിതത്തെ അപകേന്ദ്രസരണം (divergent) എന്നും പറയുന്നു. അനന്തഗുണിതത്തിലെ ഏതെങ്കിലും ഒരു ഘടകത്തിന്റെ മൂല്യം പൂജ്യമാണെങ്കില് ആ അനന്തഗുണിതത്തിന്റെ തന്നെ മൂല്യം പൂജ്യമാണ്. ഒരു ആംശികഗുണിതത്തിന്റെ മൂല്യം പൂജ്യത്തെ സമീപിക്കുന്നു എന്നു പറയുമ്പോള് ഘടകങ്ങള്ക്കൊന്നിനും പൂജ്യം മൂല്യമായിരിക്കുകയില്ലെന്ന് ഓര്ക്കേണ്ടതുണ്ട്. പ്രതിപാദന സൌകര്യത്തെ ഉദ്ദേശിച്ച് അനന്തഗുണിതങ്ങളെ
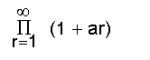
എന്ന തരത്തിലാണ് എഴുതിപ്പോരുന്നത്. അപ്പോള് P_n എന്ന ആംശികഗുണിതം
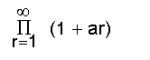
എന്നാകും. ഘടകങ്ങളെല്ലാം പൂജ്യത്തില്നിന്നു ഭിന്നമായിരിക്കുന്ന
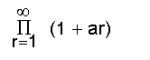
എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമാകാമെങ്കില് അവശ്യം വേണ്ടതും (necessary) മതിയായതുമായ (sufficient) ഒരു വ്യവസ്ഥ ഇതാണ്: എന്ന ധനരാശി എത്ര ചെറുതായിരുന്നാലും, ിച0 ആണെങ്കില്, m = 1, 2, 3... എന്ന മൂല്യങ്ങള്ക്കെല്ലാം
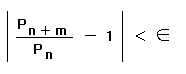
എന്ന അസമത (inequality) ഒത്തുവരത്തക്കവണ്ണം N_0 എന്നൊരു പൂര്ണസംഖ്യ കണ്ടെത്തുവാന് കഴിയണം. ഈ പ്രസ്താവനയിലെ m-ന് 1 എന്ന മൂല്യം കല്പിക്കുന്നതായാല്
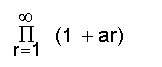
എന്ന അഭികേന്ദ്രസരണ-അനന്തഗുണിതത്തില് an+1 പൂജ്യത്തെ സമീപിച്ചുകൊണ്ടിരിക്കുമെന്നു സിദ്ധിക്കുന്നു. ഈ നിബന്ധന അഭികേന്ദ്രസരണത്തിനു വേണ്ടതാണ്; പക്ഷേ മതിയാകുന്നതല്ല.അനന്തഗുണിതങ്ങളെ സംബന്ധിച്ചുള്ള ചില പ്രമേയങ്ങള് (theorems) ചുവടെ ചേര്ക്കുന്നു. ഇവിടെ എല്ലാ മൃ-ഉം വാസ്തവികസംഖ്യകള് (real numbers) ആണെന്നു സങ്കല്പിച്ചിരിക്കുകയാണ്.
പ്രമേയം-1. എല്ലാ ar-ഉം ധനാത്മകമാണെന്നിരിക്കട്ടെ. അപ്പോള് a1 + a2 + a3 + ...എന്ന അനന്തശ്രേണി അഭികേന്ദ്രസരണമാണെങ്കില്, എങ്കില് മാത്രമേ
എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കൂ.
പ്രമേയം-2.
എന്ന അനന്തഗുണിതം അല്ലെങ്കില്
എന്ന അനന്തശ്രേണി അഭികേന്ദ്രസരണമാണെങ്കില്, തീര്ച്ചയായും
എന്ന അനന്തഗുണിതവും അഭികേന്ദ്രസരണമായിരിക്കും. അഥവാ
എന്ന അനന്തശ്രേണി നിരപേക്ഷ അഭികേന്ദ്രസരണം (absolutely convergent) ആണെങ്കില്, എങ്കില് മാത്രമേ
എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കുകയുള്ളു.
പ്രമേയം-3. എല്ലാ ar-ഉം 0≤ ar < 1 എന്ന നിബന്ധന പാലിക്കുന്നുണ്ടെന്നിരിക്കട്ടെ. അപ്പോള്
അഭികേന്ദ്രസരണമാണെങ്കില്, എങ്കില് മാത്രമേ
എന്ന അനന്തഗുണിതവും അഭികേന്ദ്രസരണമായിരിക്കൂ. നോ: അനാലിസിസ്; അഭികേന്ദ്രസരണം, അപകേന്ദ്രസരണം
(ഡോ. എസ്. പരമേശ്വരന്)