This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഊർധ്വതലപ്രക്ഷേപം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Zenithal Projection) |
Mksol (സംവാദം | സംഭാവനകള്) (→Zenithal Projection) |
||
| (ഇടക്കുള്ള ഒരു പതിപ്പിലെ മാറ്റം ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 6: | വരി 6: | ||
ഭൂ-പ്രക്ഷേപ(map-projection)ങ്ങളിലെ മൂന്നു പ്രധാന വിഭാഗങ്ങളിൽ ഒന്ന്. ഊർധ്വതലപ്രക്ഷേപങ്ങളിൽ ഭൂഗോളത്തിന്റെ ഏതെങ്കിലും ഒരു ഭാഗം നിശ്ചിതബിന്ദുവിനെ കേന്ദ്രീകരിച്ചുള്ള സ്പർശകതലത്തിലേക്കു പ്രക്ഷേപണം ചെയ്യപ്പെടുന്നു. ഇങ്ങനെയുണ്ടാകുന്ന അക്ഷാംശ-രോഖാംശ ജാലികയിൽ ഓരോ രേഖയും കൃത്യമായ ദിശയെ കാണിക്കുന്നു. ഇക്കാരണത്താൽ ഊർധ്വതല പ്രക്ഷേപങ്ങളെ ദിഗംശീയം (azimuthal) എന്നു വിശേഷിപ്പിക്കാറുണ്ട്. ഈയിനം പ്രക്ഷേപങ്ങളെ കോണിക(conical) പ്രക്ഷേപങ്ങളുടെ ഒരു രൂപാന്തരമായും വിവക്ഷിക്കാറുണ്ട്. ഭൂഗോളത്തിന്റെ ഏതെങ്കിലുമൊരുവശത്ത് കമഴ്ത്തിവയ്ക്കുന്ന ഒരു കോണിന്റെ (cone)ശീർഷകോണ് ക്രമമായി വർധിപ്പിച്ച് 180º-യിലെത്തുമ്പോള് അത് അക്ഷരേഖസ്പർശിയായ ബിന്ദുവിലെ സ്പർശകതലമായി പരിണമിക്കും എന്നതിനെ ആസ്പദമാക്കിയാണ് ഈ വിവക്ഷ. | ഭൂ-പ്രക്ഷേപ(map-projection)ങ്ങളിലെ മൂന്നു പ്രധാന വിഭാഗങ്ങളിൽ ഒന്ന്. ഊർധ്വതലപ്രക്ഷേപങ്ങളിൽ ഭൂഗോളത്തിന്റെ ഏതെങ്കിലും ഒരു ഭാഗം നിശ്ചിതബിന്ദുവിനെ കേന്ദ്രീകരിച്ചുള്ള സ്പർശകതലത്തിലേക്കു പ്രക്ഷേപണം ചെയ്യപ്പെടുന്നു. ഇങ്ങനെയുണ്ടാകുന്ന അക്ഷാംശ-രോഖാംശ ജാലികയിൽ ഓരോ രേഖയും കൃത്യമായ ദിശയെ കാണിക്കുന്നു. ഇക്കാരണത്താൽ ഊർധ്വതല പ്രക്ഷേപങ്ങളെ ദിഗംശീയം (azimuthal) എന്നു വിശേഷിപ്പിക്കാറുണ്ട്. ഈയിനം പ്രക്ഷേപങ്ങളെ കോണിക(conical) പ്രക്ഷേപങ്ങളുടെ ഒരു രൂപാന്തരമായും വിവക്ഷിക്കാറുണ്ട്. ഭൂഗോളത്തിന്റെ ഏതെങ്കിലുമൊരുവശത്ത് കമഴ്ത്തിവയ്ക്കുന്ന ഒരു കോണിന്റെ (cone)ശീർഷകോണ് ക്രമമായി വർധിപ്പിച്ച് 180º-യിലെത്തുമ്പോള് അത് അക്ഷരേഖസ്പർശിയായ ബിന്ദുവിലെ സ്പർശകതലമായി പരിണമിക്കും എന്നതിനെ ആസ്പദമാക്കിയാണ് ഈ വിവക്ഷ. | ||
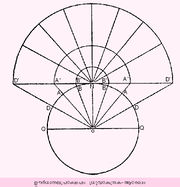
| - | [[ചിത്രം: | + | [[ചിത്രം:Vol4_789_1.jpg|thumb|ഊർധ്വതലപ്രക്ഷേപം: ധ്രുവകേന്ദ്രക-ആരേഖം]] |
ദർശനരേഖാ(perspective) സമ്പ്രദായത്തിലൂടെ ഊർധ്വതലപ്രക്ഷേപങ്ങള് നിർമിക്കാവുന്നതാണ്. ഈവിധ സമ്പ്രദായങ്ങള് നിയതമായ ജ്യാമതീയവിധികള് ഉള്ക്കൊള്ളുന്നവയുമാണ്. പ്രക്ഷേപണതലം ധ്രുവങ്ങളെയോ മധ്യരേഖയിലെ ഏതെങ്കിലും ഒരു ബിന്ദുവിനെയോ അതുമല്ലെങ്കിൽ ഗോളോപരിതലത്തിലെ ഏതെങ്കിലും ഒരു ബിന്ദുവിനെയോ സ്പർശിക്കുന്ന തരത്തിൽ പ്രതിഷ്ഠിക്കാവുന്നതാണ്; സ്പർശബിന്ദുവിനെ അടിസ്ഥാനമാക്കി ഊർധ്വതലപ്രക്ഷേപങ്ങള് ധ്രുവീയം (polar), മധ്യരേഖീയം(equatorial), തിര്യക് (oblique) എന്നിങ്ങനെ വർഗീകൃതമാകുന്നു. ഇതിൽനിന്നും ഭൂമിയുടെ ഏതു ഭാഗത്തിന്റെയും മാനചിത്രത്തിന് ഈയിനം പ്രക്ഷേപങ്ങള് ഉപയോഗിക്കാവുന്നതാണെന്നു കാണാം. എന്നാൽ ഭൂഗോളത്തിന്റെ ഒന്നാകെയുള്ള പ്രതിനിധാനം ഇവയിലൂടെ സാധ്യമാവുന്നില്ല. | ദർശനരേഖാ(perspective) സമ്പ്രദായത്തിലൂടെ ഊർധ്വതലപ്രക്ഷേപങ്ങള് നിർമിക്കാവുന്നതാണ്. ഈവിധ സമ്പ്രദായങ്ങള് നിയതമായ ജ്യാമതീയവിധികള് ഉള്ക്കൊള്ളുന്നവയുമാണ്. പ്രക്ഷേപണതലം ധ്രുവങ്ങളെയോ മധ്യരേഖയിലെ ഏതെങ്കിലും ഒരു ബിന്ദുവിനെയോ അതുമല്ലെങ്കിൽ ഗോളോപരിതലത്തിലെ ഏതെങ്കിലും ഒരു ബിന്ദുവിനെയോ സ്പർശിക്കുന്ന തരത്തിൽ പ്രതിഷ്ഠിക്കാവുന്നതാണ്; സ്പർശബിന്ദുവിനെ അടിസ്ഥാനമാക്കി ഊർധ്വതലപ്രക്ഷേപങ്ങള് ധ്രുവീയം (polar), മധ്യരേഖീയം(equatorial), തിര്യക് (oblique) എന്നിങ്ങനെ വർഗീകൃതമാകുന്നു. ഇതിൽനിന്നും ഭൂമിയുടെ ഏതു ഭാഗത്തിന്റെയും മാനചിത്രത്തിന് ഈയിനം പ്രക്ഷേപങ്ങള് ഉപയോഗിക്കാവുന്നതാണെന്നു കാണാം. എന്നാൽ ഭൂഗോളത്തിന്റെ ഒന്നാകെയുള്ള പ്രതിനിധാനം ഇവയിലൂടെ സാധ്യമാവുന്നില്ല. | ||
ഏതെങ്കിലുമൊരു പ്രകാശബിന്ദുവിനെ കേന്ദ്രീകരിച്ചുള്ള പ്രക്ഷേപണമാണ് ദർശനാരേഖ സമ്പ്രദായത്തിൽ സ്വീകരിക്കുന്നത്. പ്രക്ഷേപതലത്തിനും പ്രകാശബിന്ദുവിനും ഇടയ്ക്കുള്ള അകലത്തിന് ഏറ്റക്കുറച്ചിൽ വരുത്തി, പ്രക്ഷേപണത്തിൽ അക്ഷാംശ-രേഖാംശങ്ങളുടെ ആപേക്ഷികദൂരങ്ങളിൽ ക്രമീകരണങ്ങള് വരുത്താനാവുന്നു. പ്രകാശബിന്ദു ഭൂഗോളത്തിന്റെ കേന്ദ്രത്തിലാകാം; സ്പർശതലത്തിന്റെ വ്യാസപ്രതിമുഖ(antipodal) ബിന്ദുവിലാകാം; അതുപോലെതന്നെ അനന്തവിദൂരതയിലാണെന്നും സങ്കല്പിക്കാം. ഈ മൂന്ന് അവസ്ഥകളിലും ഉണ്ടാവുന്ന വ്യത്യസ്ത പ്രക്ഷേപങ്ങളെ യഥാക്രമം കേന്ദ്രകം(gnomonic), ത്രിവിമം (sterographic), ലംബികം (orthographic) എന്നിങ്ങനെ വിശേഷിപ്പിക്കുന്നു. സ്പർശതലത്തിന്റെ സ്വഭാവം ആധാരമാക്കിയുള്ള മൂന്നു വിഭാഗങ്ങള്ക്കും പ്രകാശബിന്ദുവിന്റെ സ്ഥാനം അടിസ്ഥാനമാക്കിയുള്ള ഉപവിഭാഗങ്ങളും ഉണ്ടായിരിക്കും. | ഏതെങ്കിലുമൊരു പ്രകാശബിന്ദുവിനെ കേന്ദ്രീകരിച്ചുള്ള പ്രക്ഷേപണമാണ് ദർശനാരേഖ സമ്പ്രദായത്തിൽ സ്വീകരിക്കുന്നത്. പ്രക്ഷേപതലത്തിനും പ്രകാശബിന്ദുവിനും ഇടയ്ക്കുള്ള അകലത്തിന് ഏറ്റക്കുറച്ചിൽ വരുത്തി, പ്രക്ഷേപണത്തിൽ അക്ഷാംശ-രേഖാംശങ്ങളുടെ ആപേക്ഷികദൂരങ്ങളിൽ ക്രമീകരണങ്ങള് വരുത്താനാവുന്നു. പ്രകാശബിന്ദു ഭൂഗോളത്തിന്റെ കേന്ദ്രത്തിലാകാം; സ്പർശതലത്തിന്റെ വ്യാസപ്രതിമുഖ(antipodal) ബിന്ദുവിലാകാം; അതുപോലെതന്നെ അനന്തവിദൂരതയിലാണെന്നും സങ്കല്പിക്കാം. ഈ മൂന്ന് അവസ്ഥകളിലും ഉണ്ടാവുന്ന വ്യത്യസ്ത പ്രക്ഷേപങ്ങളെ യഥാക്രമം കേന്ദ്രകം(gnomonic), ത്രിവിമം (sterographic), ലംബികം (orthographic) എന്നിങ്ങനെ വിശേഷിപ്പിക്കുന്നു. സ്പർശതലത്തിന്റെ സ്വഭാവം ആധാരമാക്കിയുള്ള മൂന്നു വിഭാഗങ്ങള്ക്കും പ്രകാശബിന്ദുവിന്റെ സ്ഥാനം അടിസ്ഥാനമാക്കിയുള്ള ഉപവിഭാഗങ്ങളും ഉണ്ടായിരിക്കും. | ||
Current revision as of 12:46, 1 ജൂലൈ 2014
ഊർധ്വതലപ്രക്ഷേപം
Zenithal Projection
ഭൂ-പ്രക്ഷേപ(map-projection)ങ്ങളിലെ മൂന്നു പ്രധാന വിഭാഗങ്ങളിൽ ഒന്ന്. ഊർധ്വതലപ്രക്ഷേപങ്ങളിൽ ഭൂഗോളത്തിന്റെ ഏതെങ്കിലും ഒരു ഭാഗം നിശ്ചിതബിന്ദുവിനെ കേന്ദ്രീകരിച്ചുള്ള സ്പർശകതലത്തിലേക്കു പ്രക്ഷേപണം ചെയ്യപ്പെടുന്നു. ഇങ്ങനെയുണ്ടാകുന്ന അക്ഷാംശ-രോഖാംശ ജാലികയിൽ ഓരോ രേഖയും കൃത്യമായ ദിശയെ കാണിക്കുന്നു. ഇക്കാരണത്താൽ ഊർധ്വതല പ്രക്ഷേപങ്ങളെ ദിഗംശീയം (azimuthal) എന്നു വിശേഷിപ്പിക്കാറുണ്ട്. ഈയിനം പ്രക്ഷേപങ്ങളെ കോണിക(conical) പ്രക്ഷേപങ്ങളുടെ ഒരു രൂപാന്തരമായും വിവക്ഷിക്കാറുണ്ട്. ഭൂഗോളത്തിന്റെ ഏതെങ്കിലുമൊരുവശത്ത് കമഴ്ത്തിവയ്ക്കുന്ന ഒരു കോണിന്റെ (cone)ശീർഷകോണ് ക്രമമായി വർധിപ്പിച്ച് 180º-യിലെത്തുമ്പോള് അത് അക്ഷരേഖസ്പർശിയായ ബിന്ദുവിലെ സ്പർശകതലമായി പരിണമിക്കും എന്നതിനെ ആസ്പദമാക്കിയാണ് ഈ വിവക്ഷ.
ദർശനരേഖാ(perspective) സമ്പ്രദായത്തിലൂടെ ഊർധ്വതലപ്രക്ഷേപങ്ങള് നിർമിക്കാവുന്നതാണ്. ഈവിധ സമ്പ്രദായങ്ങള് നിയതമായ ജ്യാമതീയവിധികള് ഉള്ക്കൊള്ളുന്നവയുമാണ്. പ്രക്ഷേപണതലം ധ്രുവങ്ങളെയോ മധ്യരേഖയിലെ ഏതെങ്കിലും ഒരു ബിന്ദുവിനെയോ അതുമല്ലെങ്കിൽ ഗോളോപരിതലത്തിലെ ഏതെങ്കിലും ഒരു ബിന്ദുവിനെയോ സ്പർശിക്കുന്ന തരത്തിൽ പ്രതിഷ്ഠിക്കാവുന്നതാണ്; സ്പർശബിന്ദുവിനെ അടിസ്ഥാനമാക്കി ഊർധ്വതലപ്രക്ഷേപങ്ങള് ധ്രുവീയം (polar), മധ്യരേഖീയം(equatorial), തിര്യക് (oblique) എന്നിങ്ങനെ വർഗീകൃതമാകുന്നു. ഇതിൽനിന്നും ഭൂമിയുടെ ഏതു ഭാഗത്തിന്റെയും മാനചിത്രത്തിന് ഈയിനം പ്രക്ഷേപങ്ങള് ഉപയോഗിക്കാവുന്നതാണെന്നു കാണാം. എന്നാൽ ഭൂഗോളത്തിന്റെ ഒന്നാകെയുള്ള പ്രതിനിധാനം ഇവയിലൂടെ സാധ്യമാവുന്നില്ല. ഏതെങ്കിലുമൊരു പ്രകാശബിന്ദുവിനെ കേന്ദ്രീകരിച്ചുള്ള പ്രക്ഷേപണമാണ് ദർശനാരേഖ സമ്പ്രദായത്തിൽ സ്വീകരിക്കുന്നത്. പ്രക്ഷേപതലത്തിനും പ്രകാശബിന്ദുവിനും ഇടയ്ക്കുള്ള അകലത്തിന് ഏറ്റക്കുറച്ചിൽ വരുത്തി, പ്രക്ഷേപണത്തിൽ അക്ഷാംശ-രേഖാംശങ്ങളുടെ ആപേക്ഷികദൂരങ്ങളിൽ ക്രമീകരണങ്ങള് വരുത്താനാവുന്നു. പ്രകാശബിന്ദു ഭൂഗോളത്തിന്റെ കേന്ദ്രത്തിലാകാം; സ്പർശതലത്തിന്റെ വ്യാസപ്രതിമുഖ(antipodal) ബിന്ദുവിലാകാം; അതുപോലെതന്നെ അനന്തവിദൂരതയിലാണെന്നും സങ്കല്പിക്കാം. ഈ മൂന്ന് അവസ്ഥകളിലും ഉണ്ടാവുന്ന വ്യത്യസ്ത പ്രക്ഷേപങ്ങളെ യഥാക്രമം കേന്ദ്രകം(gnomonic), ത്രിവിമം (sterographic), ലംബികം (orthographic) എന്നിങ്ങനെ വിശേഷിപ്പിക്കുന്നു. സ്പർശതലത്തിന്റെ സ്വഭാവം ആധാരമാക്കിയുള്ള മൂന്നു വിഭാഗങ്ങള്ക്കും പ്രകാശബിന്ദുവിന്റെ സ്ഥാനം അടിസ്ഥാനമാക്കിയുള്ള ഉപവിഭാഗങ്ങളും ഉണ്ടായിരിക്കും.
ദിഗംശങ്ങള് കൃത്യമായി കാണിക്കുന്നു എന്നതാണ് ഊർധ്വതലപ്രക്ഷേപങ്ങളുടെ പ്രധാനഗുണം. കേന്ദ്രത്തിൽനിന്നുള്ള അകലത്തിന് ആനുപാതികമായി അളവിലും ആകൃതിയിലും വിരൂപണം(distortion) ഏർപ്പെടുന്നു. പ്രക്ഷേപകേന്ദ്രത്തിലൂടെ കടന്നുപോകുന്ന ഏതു ഗുരുവൃത്തവും നേർരേഖകളായി പ്രതിനിധാനം ചെയ്യപ്പെടുന്നതുമൂലം ഏതെങ്കിലും പ്രത്യേകസ്ഥാനം കേന്ദ്രമാക്കിയുള്ള നാവിക-വ്യോമയാന ചാർട്ടുകള്ക്ക് ഇവ അത്യുത്തമമാണ്. നോ. ഭൂപ്രക്ഷേപം
(പി.ജി. വിഷ്ണുകുമാരി; സ.പ.)