This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഉത്തോലകം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Lever) |
Mksol (സംവാദം | സംഭാവനകള്) (→Lever) |
||
| വരി 2: | വരി 2: | ||
==ഉത്തോലകം== | ==ഉത്തോലകം== | ||
==Lever== | ==Lever== | ||
| - | [[ചിത്രം: | + | [[ചിത്രം:Vol4_599_1.jpg|thumb|ചിത്രം 1 |
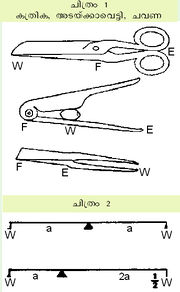
കത്രിക, അടയ്ക്കാവെട്ടി, ചവണ]] | കത്രിക, അടയ്ക്കാവെട്ടി, ചവണ]] | ||
ഭാരോദ്വഹനത്തെ ലഘൂകരിക്കുന്ന ഒരു യാന്ത്രികോപകരണം. സ്വയം ഉയർത്താന് കഴിയാത്ത ഭാര(weight)ത്തെ ഇതിന്റെ സഹായത്തോടെ എളുപ്പത്തിൽ ഉയർത്താന് സാധിക്കുന്നതാണ്. ഇതുപയോഗിക്കുമ്പോള് സ്വയം ഉയർത്തുന്നതിലേറെ സമയമെടുക്കുമെങ്കിലും കൂടുതൽ ഭാരം ഉയർത്താന് ഇതുകൊണ്ടു സാധിക്കുന്നതാണ്; യാന്ത്രികമായ യത്നലാഭവും അനുഭവപ്പെടുന്നു. ഒരു ബിന്ദുവിനെ ആധാരമാക്കി ചലിപ്പിക്കാവുന്ന ദൃഢമായ ഒരു ദണ്ഡു മാത്രമേ ലളിതമായ ഉത്തോലകത്തിൽ അവശ്യം ആവശ്യമുള്ളൂ. ആ ബിന്ദുവിനെ പടങ്ങ്, താങ്ങ്, ധാരം അഥവാ ആലംബം (Fulcrum) എന്നു പറയുന്നു. | ഭാരോദ്വഹനത്തെ ലഘൂകരിക്കുന്ന ഒരു യാന്ത്രികോപകരണം. സ്വയം ഉയർത്താന് കഴിയാത്ത ഭാര(weight)ത്തെ ഇതിന്റെ സഹായത്തോടെ എളുപ്പത്തിൽ ഉയർത്താന് സാധിക്കുന്നതാണ്. ഇതുപയോഗിക്കുമ്പോള് സ്വയം ഉയർത്തുന്നതിലേറെ സമയമെടുക്കുമെങ്കിലും കൂടുതൽ ഭാരം ഉയർത്താന് ഇതുകൊണ്ടു സാധിക്കുന്നതാണ്; യാന്ത്രികമായ യത്നലാഭവും അനുഭവപ്പെടുന്നു. ഒരു ബിന്ദുവിനെ ആധാരമാക്കി ചലിപ്പിക്കാവുന്ന ദൃഢമായ ഒരു ദണ്ഡു മാത്രമേ ലളിതമായ ഉത്തോലകത്തിൽ അവശ്യം ആവശ്യമുള്ളൂ. ആ ബിന്ദുവിനെ പടങ്ങ്, താങ്ങ്, ധാരം അഥവാ ആലംബം (Fulcrum) എന്നു പറയുന്നു. | ||
| + | |||
പടങ്ങുവയ്ക്കുന്ന സ്ഥാനത്തെ അപേക്ഷിച്ച് ഉത്തോലകത്തെ മൂന്നു തരമായി തിരിക്കാം. പടങ്ങ് ഭാരത്തിനും യത്നത്തിനുമിടയ്ക്കാണെങ്കിൽ ഒന്നാമത്തെ തരവും, ഭാരം യത്നത്തിനും പടങ്ങിനുമിടയ്ക്കാണെങ്കിൽ രണ്ടാമത്തെ തരവും, യത്നം (effort) ഭാരത്തിനും പടങ്ങിനുമിടയ്ക്കാണെങ്കിൽ മൂന്നാമത്തെ തരവുമാണെന്നു പറയുന്നു. തടി മറിക്കാന് ഉപയോഗിക്കുന്ന വീണ്ടിയും കത്രികയും ഒന്നാമത്തെ തരം ഉത്തോലകമാണ്. വീൽബാറോ (wheelbarrow), അടയ്ക്കാവെട്ടി എന്നിവ രണ്ടാമത്തെ തരവും ചവണ (forceps) മൂന്നാമത്തെ തരവും. ആർക്കിമിഡീസാണ് ഉത്തോലകത്തിന്റെ തത്ത്വം ആദ്യമായി അവതരിപ്പിച്ചത്. | പടങ്ങുവയ്ക്കുന്ന സ്ഥാനത്തെ അപേക്ഷിച്ച് ഉത്തോലകത്തെ മൂന്നു തരമായി തിരിക്കാം. പടങ്ങ് ഭാരത്തിനും യത്നത്തിനുമിടയ്ക്കാണെങ്കിൽ ഒന്നാമത്തെ തരവും, ഭാരം യത്നത്തിനും പടങ്ങിനുമിടയ്ക്കാണെങ്കിൽ രണ്ടാമത്തെ തരവും, യത്നം (effort) ഭാരത്തിനും പടങ്ങിനുമിടയ്ക്കാണെങ്കിൽ മൂന്നാമത്തെ തരവുമാണെന്നു പറയുന്നു. തടി മറിക്കാന് ഉപയോഗിക്കുന്ന വീണ്ടിയും കത്രികയും ഒന്നാമത്തെ തരം ഉത്തോലകമാണ്. വീൽബാറോ (wheelbarrow), അടയ്ക്കാവെട്ടി എന്നിവ രണ്ടാമത്തെ തരവും ചവണ (forceps) മൂന്നാമത്തെ തരവും. ആർക്കിമിഡീസാണ് ഉത്തോലകത്തിന്റെ തത്ത്വം ആദ്യമായി അവതരിപ്പിച്ചത്. | ||
| + | |||
ഏകതാനമായ (uniform) ദണ്ഡാണ് ഉപയോഗിക്കുന്നത് എങ്കിൽ പടങ്ങിനെ ആധാരമാക്കി സന്തുലനാവസ്ഥയിൽ ആയിരിക്കുമ്പോള് ദണ്ഡിന്റെ ഇരുവശങ്ങളിലേക്കുമുള്ള നീളം തുല്യമായിരിക്കും. അപ്പോള് രണ്ടറ്റത്തും തുല്യമായ ഭാരം വച്ചാൽ സന്തുലനാവസ്ഥയിൽത്തന്നെയായിരിക്കും ദണ്ഡ്. ഒരുവശം മറ്റേതിന്റെ രണ്ടിരട്ടി നീളത്തിലാണെങ്കിൽ തുല്യമായ ഭാരങ്ങള്കൊണ്ട് ദണ്ഡിനെ സന്തുലനാവസ്ഥയിൽ നിർത്തുവാന് കഴിയില്ല; നീളം കുറഞ്ഞവശത്ത് കൂടിയവശത്തുള്ളതിന്റെ രണ്ടിരട്ടി ഭാരംവച്ചാലേ സന്തുലനാവസ്ഥ പ്രാപിക്കുകയുള്ളൂ. | ഏകതാനമായ (uniform) ദണ്ഡാണ് ഉപയോഗിക്കുന്നത് എങ്കിൽ പടങ്ങിനെ ആധാരമാക്കി സന്തുലനാവസ്ഥയിൽ ആയിരിക്കുമ്പോള് ദണ്ഡിന്റെ ഇരുവശങ്ങളിലേക്കുമുള്ള നീളം തുല്യമായിരിക്കും. അപ്പോള് രണ്ടറ്റത്തും തുല്യമായ ഭാരം വച്ചാൽ സന്തുലനാവസ്ഥയിൽത്തന്നെയായിരിക്കും ദണ്ഡ്. ഒരുവശം മറ്റേതിന്റെ രണ്ടിരട്ടി നീളത്തിലാണെങ്കിൽ തുല്യമായ ഭാരങ്ങള്കൊണ്ട് ദണ്ഡിനെ സന്തുലനാവസ്ഥയിൽ നിർത്തുവാന് കഴിയില്ല; നീളം കുറഞ്ഞവശത്ത് കൂടിയവശത്തുള്ളതിന്റെ രണ്ടിരട്ടി ഭാരംവച്ചാലേ സന്തുലനാവസ്ഥ പ്രാപിക്കുകയുള്ളൂ. | ||
| + | |||
ഉത്തോലകത്തിന്റെ സാമാന്യതത്ത്വം ഇതിൽനിന്നു വ്യക്തമാകുന്നു. നീളംകൂടിയ ഭുജത്തിന്റെ അഗ്രത്തിൽ ചെലുത്തുന്ന യത്നത്തെക്കാള് കൂടുതൽ ഭാരം, നീളംകുറഞ്ഞ ഭുജത്തിന്റെ അഗ്രത്തിൽ നിർത്താമെന്ന തത്ത്വമാണ് ഉത്തോലകത്തിന്റെ പ്രവർത്തനത്തിൽ അന്തർലീനമായിരിക്കുന്നത്. പടങ്ങിനെ കേന്ദ്രമാക്കി ദണ്ഡ് തിരിയുമ്പോഴുള്ള ആഘൂർണം moment), a X w എന്നു സൂചിപ്പിക്കാം (ചിത്രം 2). രണ്ടാമത്തേതിലും ആഘൂർണം 2a x œw = a x w തന്നെയാണ്. പടങ്ങ് ഭാരത്തിന്റെ സമീപത്തേക്കടുക്കുകയും ദണ്ഡിന്റെ മറുവശത്തെ നീളം കൂടുകയുമാണെങ്കിൽ കുറഞ്ഞ യത്നംകൊണ്ട് കൂടിയ ഭാരത്തെ ഉയർത്താന് കഴിയുന്നതാണ്. വളരെ നീളംകൂടിയ ഉത്തോലകം ഉപയോഗിച്ച് ഭാരോദ്വഹനം ഇങ്ങനെ എളുപ്പമാക്കാവുന്നതാണ്. സന്തുലനാവസ്ഥയിൽ, ഭാരത്തെ ഭാരഭുജംകൊണ്ടു ഗുണിച്ചുകിട്ടുന്ന ഫലം, യത്നവും യത്നഭുജവും തമ്മിലുള്ള ഗുണനഫലത്തിനു തുല്യമായിരിക്കും. W x a = E x b; ഇതിൽ W, a, E, b എന്നിവ ക്രമത്തിൽ ഭാരം, ഭാരഭുജം, യത്നം, യത്നഭുജം ആണ്. ഉത്തോലകംകൊണ്ടുണ്ടാകുന്ന യാന്ത്രികലാഭം ഭാരത്തെ യത്നംകൊണ്ട് ഹരിച്ചുകിട്ടുന്ന ഫലമായി നിർവചിച്ചിരിക്കുന്നു; ഇതുതന്നെയാണ് യത്നഭുജത്തെ ഭാരഭുജംകൊണ്ടു ഹരിച്ചുകിട്ടുന്ന ഫലവും. ഈ സംവിധാനംകൊണ്ട് യത്നത്തിൽ കുറവുണ്ടെങ്കിലും പ്രയുക്തമാകുന്ന ഊർജത്തിൽ ലാഭമുണ്ടാകുന്നില്ല. ഇതിൽ കുറച്ചു യത്നം കൂടുതൽ സമയത്തേക്കു പ്രയോഗിക്കേണ്ടിവരുന്നു. | ഉത്തോലകത്തിന്റെ സാമാന്യതത്ത്വം ഇതിൽനിന്നു വ്യക്തമാകുന്നു. നീളംകൂടിയ ഭുജത്തിന്റെ അഗ്രത്തിൽ ചെലുത്തുന്ന യത്നത്തെക്കാള് കൂടുതൽ ഭാരം, നീളംകുറഞ്ഞ ഭുജത്തിന്റെ അഗ്രത്തിൽ നിർത്താമെന്ന തത്ത്വമാണ് ഉത്തോലകത്തിന്റെ പ്രവർത്തനത്തിൽ അന്തർലീനമായിരിക്കുന്നത്. പടങ്ങിനെ കേന്ദ്രമാക്കി ദണ്ഡ് തിരിയുമ്പോഴുള്ള ആഘൂർണം moment), a X w എന്നു സൂചിപ്പിക്കാം (ചിത്രം 2). രണ്ടാമത്തേതിലും ആഘൂർണം 2a x œw = a x w തന്നെയാണ്. പടങ്ങ് ഭാരത്തിന്റെ സമീപത്തേക്കടുക്കുകയും ദണ്ഡിന്റെ മറുവശത്തെ നീളം കൂടുകയുമാണെങ്കിൽ കുറഞ്ഞ യത്നംകൊണ്ട് കൂടിയ ഭാരത്തെ ഉയർത്താന് കഴിയുന്നതാണ്. വളരെ നീളംകൂടിയ ഉത്തോലകം ഉപയോഗിച്ച് ഭാരോദ്വഹനം ഇങ്ങനെ എളുപ്പമാക്കാവുന്നതാണ്. സന്തുലനാവസ്ഥയിൽ, ഭാരത്തെ ഭാരഭുജംകൊണ്ടു ഗുണിച്ചുകിട്ടുന്ന ഫലം, യത്നവും യത്നഭുജവും തമ്മിലുള്ള ഗുണനഫലത്തിനു തുല്യമായിരിക്കും. W x a = E x b; ഇതിൽ W, a, E, b എന്നിവ ക്രമത്തിൽ ഭാരം, ഭാരഭുജം, യത്നം, യത്നഭുജം ആണ്. ഉത്തോലകംകൊണ്ടുണ്ടാകുന്ന യാന്ത്രികലാഭം ഭാരത്തെ യത്നംകൊണ്ട് ഹരിച്ചുകിട്ടുന്ന ഫലമായി നിർവചിച്ചിരിക്കുന്നു; ഇതുതന്നെയാണ് യത്നഭുജത്തെ ഭാരഭുജംകൊണ്ടു ഹരിച്ചുകിട്ടുന്ന ഫലവും. ഈ സംവിധാനംകൊണ്ട് യത്നത്തിൽ കുറവുണ്ടെങ്കിലും പ്രയുക്തമാകുന്ന ഊർജത്തിൽ ലാഭമുണ്ടാകുന്നില്ല. ഇതിൽ കുറച്ചു യത്നം കൂടുതൽ സമയത്തേക്കു പ്രയോഗിക്കേണ്ടിവരുന്നു. | ||
Current revision as of 10:31, 1 ജൂലൈ 2014
ഉത്തോലകം
Lever
ഭാരോദ്വഹനത്തെ ലഘൂകരിക്കുന്ന ഒരു യാന്ത്രികോപകരണം. സ്വയം ഉയർത്താന് കഴിയാത്ത ഭാര(weight)ത്തെ ഇതിന്റെ സഹായത്തോടെ എളുപ്പത്തിൽ ഉയർത്താന് സാധിക്കുന്നതാണ്. ഇതുപയോഗിക്കുമ്പോള് സ്വയം ഉയർത്തുന്നതിലേറെ സമയമെടുക്കുമെങ്കിലും കൂടുതൽ ഭാരം ഉയർത്താന് ഇതുകൊണ്ടു സാധിക്കുന്നതാണ്; യാന്ത്രികമായ യത്നലാഭവും അനുഭവപ്പെടുന്നു. ഒരു ബിന്ദുവിനെ ആധാരമാക്കി ചലിപ്പിക്കാവുന്ന ദൃഢമായ ഒരു ദണ്ഡു മാത്രമേ ലളിതമായ ഉത്തോലകത്തിൽ അവശ്യം ആവശ്യമുള്ളൂ. ആ ബിന്ദുവിനെ പടങ്ങ്, താങ്ങ്, ധാരം അഥവാ ആലംബം (Fulcrum) എന്നു പറയുന്നു.
പടങ്ങുവയ്ക്കുന്ന സ്ഥാനത്തെ അപേക്ഷിച്ച് ഉത്തോലകത്തെ മൂന്നു തരമായി തിരിക്കാം. പടങ്ങ് ഭാരത്തിനും യത്നത്തിനുമിടയ്ക്കാണെങ്കിൽ ഒന്നാമത്തെ തരവും, ഭാരം യത്നത്തിനും പടങ്ങിനുമിടയ്ക്കാണെങ്കിൽ രണ്ടാമത്തെ തരവും, യത്നം (effort) ഭാരത്തിനും പടങ്ങിനുമിടയ്ക്കാണെങ്കിൽ മൂന്നാമത്തെ തരവുമാണെന്നു പറയുന്നു. തടി മറിക്കാന് ഉപയോഗിക്കുന്ന വീണ്ടിയും കത്രികയും ഒന്നാമത്തെ തരം ഉത്തോലകമാണ്. വീൽബാറോ (wheelbarrow), അടയ്ക്കാവെട്ടി എന്നിവ രണ്ടാമത്തെ തരവും ചവണ (forceps) മൂന്നാമത്തെ തരവും. ആർക്കിമിഡീസാണ് ഉത്തോലകത്തിന്റെ തത്ത്വം ആദ്യമായി അവതരിപ്പിച്ചത്.
ഏകതാനമായ (uniform) ദണ്ഡാണ് ഉപയോഗിക്കുന്നത് എങ്കിൽ പടങ്ങിനെ ആധാരമാക്കി സന്തുലനാവസ്ഥയിൽ ആയിരിക്കുമ്പോള് ദണ്ഡിന്റെ ഇരുവശങ്ങളിലേക്കുമുള്ള നീളം തുല്യമായിരിക്കും. അപ്പോള് രണ്ടറ്റത്തും തുല്യമായ ഭാരം വച്ചാൽ സന്തുലനാവസ്ഥയിൽത്തന്നെയായിരിക്കും ദണ്ഡ്. ഒരുവശം മറ്റേതിന്റെ രണ്ടിരട്ടി നീളത്തിലാണെങ്കിൽ തുല്യമായ ഭാരങ്ങള്കൊണ്ട് ദണ്ഡിനെ സന്തുലനാവസ്ഥയിൽ നിർത്തുവാന് കഴിയില്ല; നീളം കുറഞ്ഞവശത്ത് കൂടിയവശത്തുള്ളതിന്റെ രണ്ടിരട്ടി ഭാരംവച്ചാലേ സന്തുലനാവസ്ഥ പ്രാപിക്കുകയുള്ളൂ.
ഉത്തോലകത്തിന്റെ സാമാന്യതത്ത്വം ഇതിൽനിന്നു വ്യക്തമാകുന്നു. നീളംകൂടിയ ഭുജത്തിന്റെ അഗ്രത്തിൽ ചെലുത്തുന്ന യത്നത്തെക്കാള് കൂടുതൽ ഭാരം, നീളംകുറഞ്ഞ ഭുജത്തിന്റെ അഗ്രത്തിൽ നിർത്താമെന്ന തത്ത്വമാണ് ഉത്തോലകത്തിന്റെ പ്രവർത്തനത്തിൽ അന്തർലീനമായിരിക്കുന്നത്. പടങ്ങിനെ കേന്ദ്രമാക്കി ദണ്ഡ് തിരിയുമ്പോഴുള്ള ആഘൂർണം moment), a X w എന്നു സൂചിപ്പിക്കാം (ചിത്രം 2). രണ്ടാമത്തേതിലും ആഘൂർണം 2a x œw = a x w തന്നെയാണ്. പടങ്ങ് ഭാരത്തിന്റെ സമീപത്തേക്കടുക്കുകയും ദണ്ഡിന്റെ മറുവശത്തെ നീളം കൂടുകയുമാണെങ്കിൽ കുറഞ്ഞ യത്നംകൊണ്ട് കൂടിയ ഭാരത്തെ ഉയർത്താന് കഴിയുന്നതാണ്. വളരെ നീളംകൂടിയ ഉത്തോലകം ഉപയോഗിച്ച് ഭാരോദ്വഹനം ഇങ്ങനെ എളുപ്പമാക്കാവുന്നതാണ്. സന്തുലനാവസ്ഥയിൽ, ഭാരത്തെ ഭാരഭുജംകൊണ്ടു ഗുണിച്ചുകിട്ടുന്ന ഫലം, യത്നവും യത്നഭുജവും തമ്മിലുള്ള ഗുണനഫലത്തിനു തുല്യമായിരിക്കും. W x a = E x b; ഇതിൽ W, a, E, b എന്നിവ ക്രമത്തിൽ ഭാരം, ഭാരഭുജം, യത്നം, യത്നഭുജം ആണ്. ഉത്തോലകംകൊണ്ടുണ്ടാകുന്ന യാന്ത്രികലാഭം ഭാരത്തെ യത്നംകൊണ്ട് ഹരിച്ചുകിട്ടുന്ന ഫലമായി നിർവചിച്ചിരിക്കുന്നു; ഇതുതന്നെയാണ് യത്നഭുജത്തെ ഭാരഭുജംകൊണ്ടു ഹരിച്ചുകിട്ടുന്ന ഫലവും. ഈ സംവിധാനംകൊണ്ട് യത്നത്തിൽ കുറവുണ്ടെങ്കിലും പ്രയുക്തമാകുന്ന ഊർജത്തിൽ ലാഭമുണ്ടാകുന്നില്ല. ഇതിൽ കുറച്ചു യത്നം കൂടുതൽ സമയത്തേക്കു പ്രയോഗിക്കേണ്ടിവരുന്നു.