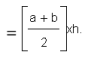This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
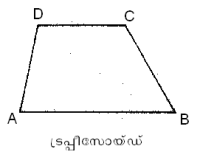
ട്രപ്പീസോയ്ഡ്
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
(→ട്രപ്പീസോയ്ഡ്) |
(→ട്രപ്പീസോയ്ഡ്) |
||
| (ഇടക്കുള്ള 8 പതിപ്പുകളിലെ മാറ്റങ്ങള്‍ ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 2: | വരി 2: | ||
Trapezoid | Trapezoid | ||
| - | + | [[Image:pno444.png|left]]രണ്ടു വശങ്ങള്‍ സമാന്തരവും മറ്റു രണ്ടു വശങ്ങള്‍ സമാന്തരമല്ലാത്തതുമായ ചതുര്‍ഭുജം. സമാന്തരമല്ലാത്ത വശങ്ങളുടെ നീളം തുല്യമാണെങ്കില്‍ ഇതിനെ സമദ്വിഭുജ ട്രപ്പീസോയ്ഡ് (isosceles trapezoid) എന്നു പറയുന്നു. ഒരു ട്രപ്പീസോയ്ഡിന്റെ സമാന്തര വശങ്ങളുടെ നീളം a, bയും അവ തമ്മിലുള്ള അകലം (ലംബം) h ഉം ആയാല്‍ വിസ്തീര്‍ണം | |
| - | മറ്റു രണ്ടു വശങ്ങള്‍ സമാന്തരമല്ലാത്തതുമായ ചതുര്‍ഭുജം. സമാന്തരമല്ലാത്ത വശങ്ങളുടെ നീളം തുല്യമാണെങ്കില്‍ ഇതിനെ സമദ്വിഭുജ ട്രപ്പീസോയ്ഡ് (isosceles trapezoid) എന്നു പറയുന്നു. ഒരു ട്രപ്പീസോയ്ഡിന്റെ സമാന്തര വശങ്ങളുടെ നീളം a, bയും അവ തമ്മിലുള്ള അകലം (ലംബം) h ഉം ആയാല്‍ വിസ്തീര്‍ണം | + | [[Image:444formula5.png]] |
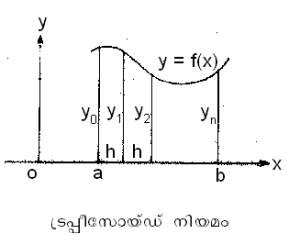
'''ട്രപ്പീസോയ്ഡ് നിയമം.''' X അക്ഷത്തിനു ലംബമായ രണ്ടു കോടി (ordinate) കള്‍ക്കിടയില്‍ ഒരു വക്രം ഉള്‍ക്കൊള്ളുന്ന ഏകദേശ വിസ്തീര്‍ണം നിര്‍ണയിക്കാനുള്ള സൂത്രവാക്യം. വിസ്തീര്‍ണം കണ്ടുപിടിക്കേണ്ട ഭാഗത്തെ X അക്ഷത്തിനു ലംബമായ ട്രപ്പീസോയ്ഡുകളായി (കോളങ്ങളായി) വിഭജിച്ച് അവ ഓരോന്നിന്റേയും വിസ്തീര്‍ണങ്ങള്‍ തമ്മില്‍ കൂട്ടിയാണ് ആകെ വിസ്തീര്‍ണം കണക്കാക്കുന്നത്. | '''ട്രപ്പീസോയ്ഡ് നിയമം.''' X അക്ഷത്തിനു ലംബമായ രണ്ടു കോടി (ordinate) കള്‍ക്കിടയില്‍ ഒരു വക്രം ഉള്‍ക്കൊള്ളുന്ന ഏകദേശ വിസ്തീര്‍ണം നിര്‍ണയിക്കാനുള്ള സൂത്രവാക്യം. വിസ്തീര്‍ണം കണ്ടുപിടിക്കേണ്ട ഭാഗത്തെ X അക്ഷത്തിനു ലംബമായ ട്രപ്പീസോയ്ഡുകളായി (കോളങ്ങളായി) വിഭജിച്ച് അവ ഓരോന്നിന്റേയും വിസ്തീര്‍ണങ്ങള്‍ തമ്മില്‍ കൂട്ടിയാണ് ആകെ വിസ്തീര്‍ണം കണക്കാക്കുന്നത്. | ||
| - | [[Image: | + | |
| - | y = f(x) എന്ന വക്രം x=a, x=b എന്നിവയിലെ കോടികള്‍ക്കിടയില്‍ ഉള്‍ക്കൊള്ളുന്ന ഏകദേശ വിസ്തീര്‍ണം, A= | + | [[Image:pno444a.png|left]] |
| - | +y<sub>n-1</sub>)y<sub>m</sub>]ഇവിടെ തുല്യ ഉപ അന്തരാള (sub-interval)ങ്ങളുടെ നീളം h- | + | |
| + | y = f(x) എന്ന വക്രം x=a, x=b എന്നിവയിലെ കോടികള്‍ക്കിടയില്‍ ഉള്‍ക്കൊള്ളുന്ന ഏകദേശ വിസ്തീര്‍ണം,<math>A=\frac{h}{2}</math>[y<sub>0</sub>+2(y<sub>1</sub>+y<sub>2</sub>+...... | ||
| + | +y<sub>n-1</sub>)y<sub>m</sub>]ഇവിടെ തുല്യ ഉപ അന്തരാള (sub-interval)ങ്ങളുടെ നീളം h-ഉംy<sub>0</sub>,y<sub>1</sub>,y<sub>2</sub>,....y<sub>n</sub>ഇവ (n+1) കോടികളുമാണ്. | ||
(പ്രൊ.കെ.ജയചന്ദ്രന്‍) | (പ്രൊ.കെ.ജയചന്ദ്രന്‍) | ||
Current revision as of 09:14, 12 ജനുവരി 2009
ട്രപ്പീസോയ്ഡ്
Trapezoid
ട്രപ്പീസോയ്ഡ് നിയമം. X അക്ഷത്തിനു ലംബമായ രണ്ടു കോടി (ordinate) കള്‍ക്കിടയില്‍ ഒരു വക്രം ഉള്‍ക്കൊള്ളുന്ന ഏകദേശ വിസ്തീര്‍ണം നിര്‍ണയിക്കാനുള്ള സൂത്രവാക്യം. വിസ്തീര്‍ണം കണ്ടുപിടിക്കേണ്ട ഭാഗത്തെ X അക്ഷത്തിനു ലംബമായ ട്രപ്പീസോയ്ഡുകളായി (കോളങ്ങളായി) വിഭജിച്ച് അവ ഓരോന്നിന്റേയും വിസ്തീര്‍ണങ്ങള്‍ തമ്മില്‍ കൂട്ടിയാണ് ആകെ വിസ്തീര്‍ണം കണക്കാക്കുന്നത്.
y = f(x) എന്ന വക്രം x=a, x=b എന്നിവയിലെ കോടികള്‍ക്കിടയില്‍ ഉള്‍ക്കൊള്ളുന്ന ഏകദേശ വിസ്തീര്‍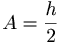ണം,
[y0+2(y1+y2+......
+yn-1)ym]ഇവിടെ തുല്യ ഉപ അന്തരാള (sub-interval)ങ്ങളുടെ നീളം h-ഉംy0,y1,y2,....ynഇവ (n+1) കോടികളുമാണ്.
(പ്രൊ.കെ.ജയചന്ദ്രന്‍)
