This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ടാന്ജെന്റ്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(New page: ടാന്ജെന്റ് ഠമിഴലി ഒരു വക്രത്തിലെ ഒരു ബിന്ദു മാത്രം ഉള്ക്കൊള്ളുന്...) |
|||
| (ഇടക്കുള്ള 30 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 1: | വരി 1: | ||
| - | ടാന്ജെന്റ് | + | =ടാന്ജെന്റ്= |
| + | Tanget | ||
| - | + | ഒരു വക്രത്തിലെ ഒരു ബിന്ദു മാത്രം ഉള്ക്കൊള്ളുന്ന രേഖയാണ് വക്രത്തിന്റെ ആ ബിന്ദുവിലെ ടാന്ജെന്റ്. ഇത് സ്പര്ശകം അഥവാ സ്പര്ശരേഖ (tangent line) എന്നും അറിയപ്പെടുന്നു. വക്രത്തില് ഒരു ബിന്ദുവിലുള്ള സ്പര്ശകം ആ ബിന്ദുവിലൂടെയുള്ള ഏതെങ്കിലും ഛേദകരേഖ(secant)യുടെ സീമാന്തസ്ഥാന (limiting position)മായി കരുതാവുന്നതാണ്. | |
| - | + | [[Image:pno72TT.png|left]] | |
| - | + | ദ്വിവിമീയ സ്പേസില് y=f (x) എന്ന വക്രത്തിലെ P(x,y) എന്ന ബിന്ദുവിലെ സ്പര്ശകം X-അക്ഷത്തിന്റെ ധനാത്മകദിശയുമായി ചരിഞ്ഞിരിക്കുന്ന കോണത്തിന്റെ അളവ് θആയാല് tanθ=f '(x).Tan θ യെ സ്പര്ശകത്തിന്റെ ചരിവ് (slope) എന്നു പറയുന്നു. ചരിവിനെ കുറിക്കാന് 'm' എന്ന പ്രതീകമുപയോഗിച്ചാല് m = f ' (x) എന്നു കിട്ടുന്നു. വക്രത്തിലെ (x<sub>1</sub>, y<sub>1</sub>) എന്ന ബിന്ദുവിലുള്ള സ്പര്ശകത്തിന്റെ സമീകരണമാണ് y - y<sub>1</sub> = f ' (x<sub>1</sub>) (x-x<sub>1</sub>). | |
| - | + | ഉദാഹരണമായി x<sup>2</sup> + y<sup>2</sup> = a<sup>2</sup> എന്ന വൃത്തത്തിലെ (x<sub>1</sub>, y<sub>1</sub>) എന്ന ബിന്ദുവില് വരയ്ക്കുന്ന സ്പര്ശകത്തിന്റെ സമീകരണമാണ് xx<sub>1</sub> + yy<sub>1</sub> = a<sup>2</sup>. പരാബൊളയുടെ മാനക സമീകരണം y<sup>2</sup> = 4ax. ഇതിലെ (x<sub>1</sub>, y<sub>1</sub>) എന്ന ബിന്ദുവിലുള്ള സ്പര്ശകത്തിന്റെ സമീകരണം yy<sub>1</sub> = 2a (x + x<sub>1</sub>) ആണ്. | |
| - | എന്ന | + | ഒരു വക്രത്തിലെ P (x,y) എന്ന ബിന്ദുവിലെ സ്പര്ശകം X അക്ഷത്തെ T എന്ന ബിന്ദുവില് പ്രതിച്ഛേദിച്ചാല് P യും T യും തമ്മിലുള്ള ദൂരത്തെ സ്പര്ശക ദൂരം (length of the tangent) എന്നു പറയുന്നു. |
| - | + | '''സ്പര്ശതലം (tangent plane).''' ഒരു പ്രതല(surface)ത്തിലുള്ള P എന്ന ബിന്ദുവില് ഒരു രേഖ സ്പര്ശകമാകണമെങ്കില് ആ ബിന്ദുവില്ക്കൂടി കടന്നുപോകുന്ന ഒരു വക്രത്തിന് (പ്രതലത്തിലുള്ളത്) ഈ രേഖ സ്പര്ശകമായിരിക്കണം. p യില്ക്കൂടി കടന്നുപോകുന്ന എല്ലാ സ്പര്ശകങ്ങളും ഉള്ള സമതലത്തെ സ്പര്ശതലം എന്നു പറയുന്നു. f (x,y,z) = 0 എന്ന പ്രതലത്തിലെ (x <sub>1</sub>,y<sub>1</sub>,z<sub>1</sub>) എന്ന ബിന്ദുവിലെ സ്പര്ശതലത്തിന്റെ സമീകരണമാണ് f<sub>1</sub>(x<sub>1</sub>,y<sub>1</sub>,z<sub>1</sub>) (x - x<sub>1</sub>) + f<sub>2</sub> (x<sub>1</sub>,y<sub>1</sub>,z<sub>1</sub>) (y - y<sub>1</sub>1) + f<sub>3</sub> (x<sub>1</sub>,y<sub>1</sub>,z<sub>1</sub>) (z-z<sub>1</sub>1)=0. | |
| - | + | ഇതില്f<sub>1</sub>,f<sub>2</sub>,f<sub>3</sub>എന്നിവ(x<sub>1</sub>,y<sub>1</sub>,z<sub>1</sub>)ലെ f ന്റെ x,y,z കൊണ്ടുള്ള ആംശിക (partial) അവകലജങ്ങളാണ്. ഉദാഹരണത്തിന് x<sup>2</sup> + y<sup>2</sup> +z<sup>2</sup> = a<sup>2</sup> എന്ന ഗോളത്തിന്റെ (x<sub>1</sub>y<sub>1</sub>z<sub>1</sub>) എന്ന ബിന്ദുവിലെ സ്പര്ശതലമാണ് x x<sub>1</sub> + yy<sub>1</sub> + zz<sub>1</sub> = a<sup>2</sup>. | |
| - | + | '''ടാന്ജെന്റ് ഫലനം (tangent function).''' സമകോണിക കാര്ട്ടീഷ്യന് തലത്തില് P(x,y) ഏതെങ്കിലും ബിന്ദുവും | |
| + | ∠ XOP = A യും ആയാല് അ യുടെ ടാന്ജെന്റ് ഫലനം <math>tan A = \frac{ y}{x}</math> എന്ന് എഴുതുന്നു. A-യ്ക്ക് മാറ്റം വരുന്നതനുസരിച്ച് tan A യുടെ വിലയും മാറിക്കൊണ്ടിരിക്കും. ഉദാഹരണത്തിന് tan 0°= 0 ; tan 45° = 1;tan 90°= ∞.ഏതെങ്കിലുമൊരു ത്രികോണം ABC യില് കോണങ്ങള് A, B, C യുടെ എതിര്വശങ്ങള് a,b,c ആയാല് | ||
| - | + | <math> tan \frac{B-C}{2} =\frac{b-c}{b+c}Cot\frac{A}{2}</math> | |
| - | + | ത്രികോണമിതിയില് ഇതിനെ ടാന്ജെന്റ് നിയമം (tangent law) എന്നു പറയുന്നു. ലോഗരിതം ഉപയോഗിച്ചുള്ള ത്രികോണനിര്ധാരണത്തിന് ഈ ഫോര്മുലയാണ് ഉപയോഗിക്കുന്നത്. | |
| - | + | [[Image:pno72a.png|300px]] | |
| - | + | y = tan x എന്ന ഫലനത്തിന്റെ ആലേഖ(graph)ത്തെ ടാന്ജെന്റ് വക്രം (tangent curve) എന്നു പറയുന്നു. ഇതൊരു സന്തത (continous) വക്രമല്ല. മൂലബിന്ദുവില്ക്കൂടി പോകുന്ന വക്രത്തിന്റെ ശാഖ [[Image:pno72formula2.png]] | |
| + | ഈ രേഖകള്ക്ക് അനന്തസ്പര്ശരേഖീയ (asymptotic)മാണ് (ചിത്രം നോക്കുക). | ||
| - | + | (പ്രൊ. കെ.ജയചന്ദ്രന്) | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
Current revision as of 09:39, 18 ഡിസംബര് 2008
ടാന്ജെന്റ്
Tanget
ഒരു വക്രത്തിലെ ഒരു ബിന്ദു മാത്രം ഉള്ക്കൊള്ളുന്ന രേഖയാണ് വക്രത്തിന്റെ ആ ബിന്ദുവിലെ ടാന്ജെന്റ്. ഇത് സ്പര്ശകം അഥവാ സ്പര്ശരേഖ (tangent line) എന്നും അറിയപ്പെടുന്നു. വക്രത്തില് ഒരു ബിന്ദുവിലുള്ള സ്പര്ശകം ആ ബിന്ദുവിലൂടെയുള്ള ഏതെങ്കിലും ഛേദകരേഖ(secant)യുടെ സീമാന്തസ്ഥാന (limiting position)മായി കരുതാവുന്നതാണ്.
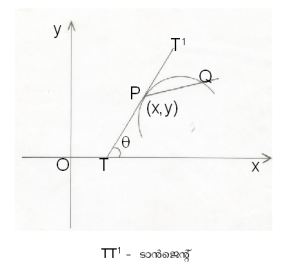
ദ്വിവിമീയ സ്പേസില് y=f (x) എന്ന വക്രത്തിലെ P(x,y) എന്ന ബിന്ദുവിലെ സ്പര്ശകം X-അക്ഷത്തിന്റെ ധനാത്മകദിശയുമായി ചരിഞ്ഞിരിക്കുന്ന കോണത്തിന്റെ അളവ് θആയാല് tanθ=f '(x).Tan θ യെ സ്പര്ശകത്തിന്റെ ചരിവ് (slope) എന്നു പറയുന്നു. ചരിവിനെ കുറിക്കാന് 'm' എന്ന പ്രതീകമുപയോഗിച്ചാല് m = f ' (x) എന്നു കിട്ടുന്നു. വക്രത്തിലെ (x1, y1) എന്ന ബിന്ദുവിലുള്ള സ്പര്ശകത്തിന്റെ സമീകരണമാണ് y - y1 = f ' (x1) (x-x1).
ഉദാഹരണമായി x2 + y2 = a2 എന്ന വൃത്തത്തിലെ (x1, y1) എന്ന ബിന്ദുവില് വരയ്ക്കുന്ന സ്പര്ശകത്തിന്റെ സമീകരണമാണ് xx1 + yy1 = a2. പരാബൊളയുടെ മാനക സമീകരണം y2 = 4ax. ഇതിലെ (x1, y1) എന്ന ബിന്ദുവിലുള്ള സ്പര്ശകത്തിന്റെ സമീകരണം yy1 = 2a (x + x1) ആണ്.
ഒരു വക്രത്തിലെ P (x,y) എന്ന ബിന്ദുവിലെ സ്പര്ശകം X അക്ഷത്തെ T എന്ന ബിന്ദുവില് പ്രതിച്ഛേദിച്ചാല് P യും T യും തമ്മിലുള്ള ദൂരത്തെ സ്പര്ശക ദൂരം (length of the tangent) എന്നു പറയുന്നു.
സ്പര്ശതലം (tangent plane). ഒരു പ്രതല(surface)ത്തിലുള്ള P എന്ന ബിന്ദുവില് ഒരു രേഖ സ്പര്ശകമാകണമെങ്കില് ആ ബിന്ദുവില്ക്കൂടി കടന്നുപോകുന്ന ഒരു വക്രത്തിന് (പ്രതലത്തിലുള്ളത്) ഈ രേഖ സ്പര്ശകമായിരിക്കണം. p യില്ക്കൂടി കടന്നുപോകുന്ന എല്ലാ സ്പര്ശകങ്ങളും ഉള്ള സമതലത്തെ സ്പര്ശതലം എന്നു പറയുന്നു. f (x,y,z) = 0 എന്ന പ്രതലത്തിലെ (x 1,y1,z1) എന്ന ബിന്ദുവിലെ സ്പര്ശതലത്തിന്റെ സമീകരണമാണ് f1(x1,y1,z1) (x - x1) + f2 (x1,y1,z1) (y - y11) + f3 (x1,y1,z1) (z-z11)=0.
ഇതില്f1,f2,f3എന്നിവ(x1,y1,z1)ലെ f ന്റെ x,y,z കൊണ്ടുള്ള ആംശിക (partial) അവകലജങ്ങളാണ്. ഉദാഹരണത്തിന് x2 + y2 +z2 = a2 എന്ന ഗോളത്തിന്റെ (x1y1z1) എന്ന ബിന്ദുവിലെ സ്പര്ശതലമാണ് x x1 + yy1 + zz1 = a2.
ടാന്ജെന്റ് ഫലനം (tangent function). സമകോണിക കാര്ട്ടീഷ്യന് തലത്തില് P(x,y) ഏതെങ്കിലും ബിന്ദുവും
∠ XOP = A യും ആയാല് അ യുടെ ടാന്ജെന്റ് ഫലനം 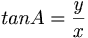 എന്ന് എഴുതുന്നു. A-യ്ക്ക് മാറ്റം വരുന്നതനുസരിച്ച് tan A യുടെ വിലയും മാറിക്കൊണ്ടിരിക്കും. ഉദാഹരണത്തിന് tan 0°= 0 ; tan 45° = 1;tan 90°= ∞.ഏതെങ്കിലുമൊരു ത്രികോണം ABC യില് കോണങ്ങള് A, B, C യുടെ എതിര്വശങ്ങള് a,b,c ആയാല്
എന്ന് എഴുതുന്നു. A-യ്ക്ക് മാറ്റം വരുന്നതനുസരിച്ച് tan A യുടെ വിലയും മാറിക്കൊണ്ടിരിക്കും. ഉദാഹരണത്തിന് tan 0°= 0 ; tan 45° = 1;tan 90°= ∞.ഏതെങ്കിലുമൊരു ത്രികോണം ABC യില് കോണങ്ങള് A, B, C യുടെ എതിര്വശങ്ങള് a,b,c ആയാല്
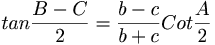
ത്രികോണമിതിയില് ഇതിനെ ടാന്ജെന്റ് നിയമം (tangent law) എന്നു പറയുന്നു. ലോഗരിതം ഉപയോഗിച്ചുള്ള ത്രികോണനിര്ധാരണത്തിന് ഈ ഫോര്മുലയാണ് ഉപയോഗിക്കുന്നത്.
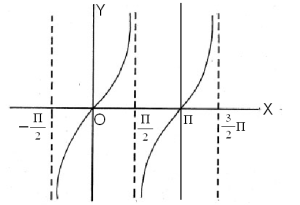
y = tan x എന്ന ഫലനത്തിന്റെ ആലേഖ(graph)ത്തെ ടാന്ജെന്റ് വക്രം (tangent curve) എന്നു പറയുന്നു. ഇതൊരു സന്തത (continous) വക്രമല്ല. മൂലബിന്ദുവില്ക്കൂടി പോകുന്ന വക്രത്തിന്റെ ശാഖ ![]() ഈ രേഖകള്ക്ക് അനന്തസ്പര്ശരേഖീയ (asymptotic)മാണ് (ചിത്രം നോക്കുക).
ഈ രേഖകള്ക്ക് അനന്തസ്പര്ശരേഖീയ (asymptotic)മാണ് (ചിത്രം നോക്കുക).
(പ്രൊ. കെ.ജയചന്ദ്രന്)