This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ട്രപ്പീസിയം (ഗണിതശാസ്ത്രം)
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
(New page: ട്രപ്പീസിയം (ഗണിതശാസ്ത്രം) ഠൃമുല്വശൌാ രണ്ട് സമാന്തര വശങ്ങളുള്ള ചതുര...) |
|||
| വരി 1: | വരി 1: | ||
| - | ട്രപ്പീസിയം (ഗണിതശാസ്ത്രം) | + | =ട്രപ്പീസിയം (ഗണിതശാസ്ത്രം)= |
| + | Trapezium | ||
| - | + | രണ്ട് സമാന്തര വശങ്ങളുള്ള ചതുര്‍ഭുജം. സമാന്തര വശങ്ങളെ ആധാരങ്ങള്‍ (bases) എന്നും അവ തമ്മിലുള്ള ലംബ അകലത്തെ ഉന്നതി (altitude) എന്നും പറയുന്നു. ഒരു ട്രപ്പീസിയത്തിന്റെ വിസ്തീര്‍ണം സമാന്തര വശങ്ങളുടെ തുകയുടെ പകുതിയെ അവ തമ്മിലുള്ള ലംബ അകലം (ഉന്നതി) കൊണ്ടു ഗുണിച്ചതിനു തുല്യമാണ്. സമാന്തര വശങ്ങള്‍ മ, യയും ഉന്നതി വഉം ആയാല്‍ ട്രപ്പീസിയത്തിന്റെ വിസ്തീര്‍ണം = [[Image:444formula1.png|200px]]ആയിരിക്കും. | |
| + | [[Image:444trapism.png|left]] | ||
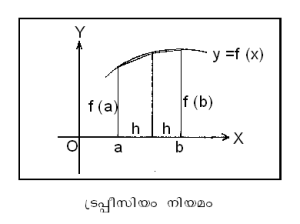
| + | '''ട്രപ്പീസിയം നിയമം (Trapezium rule).''' ഒരു വക്രം രണ്ടു കോടികള്‍ (ordinates)ക്കിടയില്‍ ഉള്‍ക്കൊള്ളുന്ന ഏകദേശ വിസ്തീര്‍ണം (approximate area) കാണാനുപയോഗിക്കുന്ന നിയമം. വിസ്തീര്‍ണം നിര്‍ണയിക്കാനുള്ള വക്രഭാഗത്തെ X അക്ഷത്തിനു ലംബമായ രണ്ടു ട്രപ്പീസിയങ്ങളായി ഭാഗിക്കുന്നു. ട്രപ്പീസിയങ്ങളുടെ വിസ്തീര്‍ണങ്ങളുടെ തുക, വക്രം ഉള്‍ക്കൊള്ളുന്ന വിസ്തീര്‍ണത്തിന്റെ ഏകദേശന(approximation)മാണ്. ഫലനം f ന്റെ വില x = a, b എന്നീ ബിന്ദുക്കളിലും ഇവയുടെ മധ്യബിന്ദുലും <math>\left(\frac{a+b}{2}\right</math>അറിയാമെങ്കില്‍ വിസ്തീര്‍ണം[[Image:444formula2.png|200px]] ന്റെ ഏകദേശമൂല്യം[[Image:444formula3.png]] | ||
| + | ആണ്. ഇവിടെ <math>h=\frac{b-a}{2}</math> . കൂടുതല്‍ സൂക്ഷ്മതയുള്ള ഏകദേശ വിസ്തീര്‍ണം കണ്ടുപിടിക്കാന്‍ വക്രത്തിന്റെ വിസ്തീര്‍ണതയുള്‍ക്കൊള്ളുന്ന ഭാഗത്തെ X അക്ഷത്തിനു ലംബമായ 4, 6, 8, ..... ട്രപ്പീസിയങ്ങളായി ഭാഗിക്കുന്നു. | ||
| - | + | (പ്രൊ. കെ. ജയചന്ദ്രന്‍) | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
05:25, 20 നവംബര്‍ 2008-നു നിലവിലുണ്ടായിരുന്ന രൂപം
ട്രപ്പീസിയം (ഗണിതശാസ്ത്രം)
Trapezium
രണ്ട് സമാന്തര വശങ്ങളുള്ള ചതുര്‍ഭുജം. സമാന്തര വശങ്ങളെ ആധാരങ്ങള്‍ (bases) എന്നും അവ തമ്മിലുള്ള ലംബ അകലത്തെ ഉന്നതി (altitude) എന്നും പറയുന്നു. ഒരു ട്രപ്പീസിയത്തിന്റെ വിസ്തീര്‍ണം സമാന്തര വശങ്ങളുടെ തുകയുടെ പകുതിയെ അവ തമ്മിലുള്ള ലംബ അകലം (ഉന്നതി) കൊണ്ടു ഗുണിച്ചതിനു തുല്യമാണ്. സമാന്തര വശങ്ങള്‍ മ, യയും ഉന്നതി വഉം ആയാല്‍ ട്രപ്പീസിയത്തിന്റെ വിസ്തീര്‍ണം =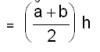 
ആയിരിക്കും.
ട്രപ്പീസിയം നിയമം (Trapezium rule). ഒരു വക്രം രണ്ടു കോടികള്‍ (ordinates)ക്കിടയില്‍ ഉള്‍ക്കൊള്ളുന്ന ഏകദേശ വിസ്തീര്‍ണം (approximate area) കാണാനുപയോഗിക്കുന്ന നിയമം. വിസ്തീര്‍ണം നിര്‍ണയിക്കാനുള്ള വക്രഭാഗത്തെ X അക്ഷത്തിനു ലംബമായ രണ്ടു ട്രപ്പീസിയങ്ങളായി ഭാഗിക്കുന്നു. ട്രപ്പീസിയങ്ങളുടെ വിസ്തീര്‍ണങ്ങളുടെ തുക, വക്രം ഉള്‍ക്കൊള്ളുന്ന വിസ്തീര്‍ണത്തിന്റെ ഏകദേശന(approximation)മാണ്. ഫലനം f ന്റെ വില x = a, b എന്നീ ബിന്ദുക്കളിലും ഇവയുടെ മധ്യബിന്ദുലും parse ചെയ്യുവാന്‍ പരാജയപ്പെട്ടു (Missing texvc executable;
please see math/README to configure.): \left(\frac{a+b}{2}\right
അറിയാമെങ്കില്‍ വിസ്തീര്‍ണം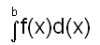
ന്റെ ഏകദേശമൂല്യം
ആണ്. ഇവിടെ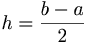 
. കൂടുതല്‍ സൂക്ഷ്മതയുള്ള ഏകദേശ വിസ്തീര്‍ണം കണ്ടുപിടിക്കാന്‍ വക്രത്തിന്റെ വിസ്തീര്‍ണതയുള്‍ക്കൊള്ളുന്ന ഭാഗത്തെ X അക്ഷത്തിനു ലംബമായ 4, 6, 8, ..... ട്രപ്പീസിയങ്ങളായി ഭാഗിക്കുന്നു.
(പ്രൊ. കെ. ജയചന്ദ്രന്‍)
