This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ടണലിങ് (ഇലക്ട്രോണികം)
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
| വരി 2: | വരി 2: | ||
Tunnelling (electronics) | Tunnelling (electronics) | ||
| - | കടന്നു പോകാന്‍ പ്രഥമദൃഷ്ട്യാ പ്രയാസമുള്ള ഊര്‍ജ രോധകങ്ങളെ ( | + | കടന്നു പോകാന്‍ പ്രഥമദൃഷ്ട്യാ പ്രയാസമുള്ള ഊര്‍ജ രോധകങ്ങളെ (energy barriers) സൂക്ഷ്മകണികകള്‍ വേധനം ചെയ്ത് പുറത്തുവരുന്ന ക്വാണ്ടം ബലതന്ത്ര പ്രതിഭാസം. രോധകവേധനം (barrier penetration) എന്നും അറിയപ്പെടുന്നു. ഒരു ഏകമാന പൊട്ടന്‍ഷ്യല്‍ കിണറില്‍ (1-D potential well) E ഊര്‍ജം ഉള്ള ഒരു സൂക്ഷ്മകണിക സ്ഥിതിചെയ്യുന്നു എന്ന് സങ്കല്‍പിക്കുക. |
| + | [[Image:pno5.png]] | ||
| + | കിണറിന്റെ പൊട്ടന്‍ഷ്യല്‍ വേധനത്തിന്റെ ഉയരം/മൂല്യം (height of the potential barrier) V<sub>0</sub> ആണെങ്കില്‍ ക്ലാസിക്കല്‍ ബലതന്ത്രപ്രകാരം V<sub>0</sub>യെ അപേക്ഷിച്ച് E ഉയര്‍ന്നിരുന്നാല്‍ മാത്രമേ കണികയ്ക്കു പുറത്തുവരാനാകു; മറിച്ചാണെങ്കില്‍ കണിക കിണറിനുള്ളില്‍ ത്തന്നെ (C) അനന്തമായി കിടക്കും. എന്നാല്‍ ക്വാണ്ടം ബലതന്ത്രപ്രകാരം V<sub>0</sub> യെക്കാള്‍ E കുറഞ്ഞിരുന്നാലും കണികയ്ക്കു കിണറിനു പുറത്തേക്കു വരാനാകും; ഇതിനുള്ള സംഭാവ്യത E യുടെ മൂല്യത്തിനനുസരിച്ച് മാറിക്കൊണ്ടിരിക്കുമെന്നു മാത്രം. E,V<sub>0</sub>എന്നിവ തമ്മിലുള്ള അന്തരം വളരെക്കുറഞ്ഞു വരുന്ന സന്ദര്‍ഭങ്ങളില്‍ ടണലിങിനുള്ള സംഭാവ്യത പരമാവധിയായിരിക്കും. ടണല്‍ ചെയ്ത് പുറത്തുവരുന്ന കണികയുടെ ഊര്‍ജം E തന്നെയായിരിക്കുകയും ചെയ്യും. | ||
| - | + | മറ്റൊരുദാഹരണത്തിലൂടെ ഇത് കൂടുതല്‍ വിശദീകരിക്കാം. ഉയരമുള്ള മലമുകളിലേക്ക് അതിന്റെ ചരിവിലൂടെ ഒരുപന്തുരുട്ടി വിട്ടാല്‍ പന്തിന്റെ സ്ഥാനംകൊണ്ട് അതിന് ലഭിക്കുന്ന ഗുരുത്വാകര്‍ഷണ പൊട്ടന്‍ഷ്യല്‍ ഊര്‍ജം പന്തിന്റെ മൊത്തം ഊര്‍ജത്തോടു തുല്യമാകുന്നതുവരെ പന്ത് മലമുകളിലേക്കുരുണ്ടു നീങ്ങുന്നു. ഊര്‍ജങ്ങള്‍ തുല്യമായാലുടന്‍ പന്ത് തിരിച്ചു പുറപ്പെട്ട സ്ഥാനത്തെ ലക്ഷ്യമാക്കി കീഴ്പ്പോട്ടുരുണ്ടു തുടങ്ങും. പന്തിന് മല കടന്ന് മറു വശത്തേക്കു പോകണമെങ്കില്‍ മലമുകളില്‍ അനുഭവപ്പെടുന്ന ഗുരുത്വാകര്‍ഷണ പൊട്ടന്‍ഷ്യല്‍ ഊര്‍ജത്തെ തരണം ചെയ്യാനുള്ള ഊര്‍ജം ലഭ്യമാവണം; അല്ലാതെ ഇടയ്ക്കുവച്ച് മല തുരന്ന് പന്തിന് മറുഭാഗത്തേക്കു പോകാനാവില്ല. ഈ ക്ലാസിക്കല്‍ സമീപനരീതിയെ അപേക്ഷിച്ച് തികച്ചും വിഭിന്നമാണ് ക്വാണ്ടം ബലതന്ത്രസമീപനം. ഇതുപ്രകാരം പന്തിന് മല തുരന്ന് മറുവശത്തേക്കും വേണമെങ്കില്‍ പോകാം. അതിനുള്ള സംഭാവ്യത വളരെ ചെറുതാ ണെങ്കിലും പൂജ്യമല്ല. പദാര്‍ഥത്തിന്റെ മാനങ്ങള്‍ വര്‍ധിക്കുന്തോറുമോ അതിനെ നഗ്നനേത്രങ്ങളാല്‍ എളുപ്പത്തില്‍ കാണാനാവുന്തോറുമോ പ്രസ്തുത സംഭാവ്യതയുടെ അളവ് കുറഞ്ഞു വരുന്നു. മറിച്ച് സൂക്ഷ്മാതീതമാനങ്ങളാണ് പദാര്‍ഥത്തിനെങ്കില്‍ (ഉദാ: ആല്‍ഫാ കണികകള്‍, ന്യയൂക്ലിയോണുകള്‍, ഇലക്ട്രോണുകള്‍) ടണലിങ് സംഭാവ്യത വളരെ ഉയര്‍ന്നതായിരിക്കും. | |
| - | + | ടണലിങ് പ്രതിഭാസത്തിലേക്ക് ശ്രദ്ധയാകര്‍ഷിച്ച പ്രഥമ സംഭവം ആല്‍ഫാ കണികാ റേഡിയോ ആക്റ്റിവിറ്റിയാണ്. അണുകേന്ദ്ര ബലത്തെ അതിജീവിച്ചു പുറത്തുവരുന്ന ആല്‍ഫാ കണികകളുടെ ഊര്‍ജം അണുകേന്ദ്ര ബലത്തെ അപേക്ഷിച്ച് തുലോം ചെറുതാണ്. അതുപോലെ എല്ലാത്തരം ആല്‍ഫാ ഉത്സര്‍ജനങ്ങളുടേയും ഊര്‍ജം 2-8 മെഗ ഇലക്ട്രോണ്‍ വോള്‍ട്ട് പരിധിയില്‍പ്പെടുമ്പോള്‍ പ്രസ്തുത ഉത്സര്‍ജനത്തിന് ജന്മം നല്‍കുന്ന അണുകേന്ദ്രങ്ങളുടെ ആയുര്‍ദൈര്‍ഘ്യത്തിന്റെ മൂല്യം 10<sup>11</sup> വര്‍ഷം- 10<sup>-6</sup>സെ. പരിധിയിലാണ് വരുന്നത്; അതായത് 4 മടങ്ങ് ഊര്‍ജവ്യത്യാസം 10<sup>24</sup> മടങ്ങ് ആയുര്‍ദൈര്‍ഘ്യ വ്യതിയാനം സൃഷ്ടി ക്കുന്നു. ഇത്തരം പ്രതിഭാസങ്ങള്‍ വിശദമാക്കാന്‍ ടണലിങ് സിദ്ധാന്തത്തിനേ കഴിയുകയുള്ളു. | |
| - | + | ടണലിങ് പ്രതിഭാസത്തെ അടിസ്ഥാനമാക്കി പ്രവര്‍ത്തിച്ച് പ്രതലങ്ങളുടെ സ്ഥാനീയ ചാലകത മാപനം ചെയ്യാനുപയോഗിക്കുന്ന ഒരുപകരണമാണ് സ്കാനിങ് ടണലിങ് സൂക്ഷ്മദര്‍ശിനി (STM). സൂക്ഷ്മദര്‍ശിനിയെ ഒരു പ്രതലത്തിലൂടെ ചലിപ്പിക്കുമ്പോള്‍ ഉപകരണത്തിലെ ടണലിങ് ധാരയില്‍ അനുഭവപ്പെടുന്ന വ്യത്യാസത്തെ വിശകലനം ചെയ്യുകവഴി പ്രതലത്തിന്റെ കണികാ ഘടനയെ വ്യക്തമാക്കുന്ന പ്രതല ടൊപോഗ്രാഫിക്ക് പ്രതിബിംബം മെനഞ്ഞെടുക്കാനാകും | |
05:43, 4 ഒക്ടോബര്‍ 2008-നു നിലവിലുണ്ടായിരുന്ന രൂപം
ടണലിങ് (ഇലക്ട്രോണികം)
Tunnelling (electronics)
കടന്നു പോകാന്‍ പ്രഥമദൃഷ്ട്യാ പ്രയാസമുള്ള ഊര്‍ജ രോധകങ്ങളെ (energy barriers) സൂക്ഷ്മകണികകള്‍ വേധനം ചെയ്ത് പുറത്തുവരുന്ന ക്വാണ്ടം ബലതന്ത്ര പ്രതിഭാസം. രോധകവേധനം (barrier penetration) എന്നും അറിയപ്പെടുന്നു. ഒരു ഏകമാന പൊട്ടന്‍ഷ്യല്‍ കിണറില്‍ (1-D potential well) E ഊര്‍ജം ഉള്ള ഒരു സൂക്ഷ്മകണിക സ്ഥിതിചെയ്യുന്നു എന്ന് സങ്കല്‍പിക്കുക.
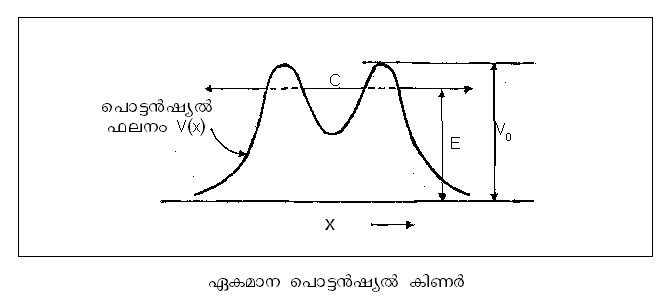കിണറിന്റെ പൊട്ടന്‍ഷ്യല്‍ വേധനത്തിന്റെ ഉയരം/മൂല്യം (height of the potential barrier) V0 ആണെങ്കില്‍ ക്ലാസിക്കല്‍ ബലതന്ത്രപ്രകാരം V0യെ അപേക്ഷിച്ച് E ഉയര്‍ന്നിരുന്നാല്‍ മാത്രമേ കണികയ്ക്കു പുറത്തുവരാനാകു; മറിച്ചാണെങ്കില്‍ കണിക കിണറിനുള്ളില്‍ ത്തന്നെ (C) അനന്തമായി കിടക്കും. എന്നാല്‍ ക്വാണ്ടം ബലതന്ത്രപ്രകാരം V0 യെക്കാള്‍ E കുറഞ്ഞിരുന്നാലും കണികയ്ക്കു കിണറിനു പുറത്തേക്കു വരാനാകും; ഇതിനുള്ള സംഭാവ്യത E യുടെ മൂല്യത്തിനനുസരിച്ച് മാറിക്കൊണ്ടിരിക്കുമെന്നു മാത്രം. E,V0എന്നിവ തമ്മിലുള്ള അന്തരം വളരെക്കുറഞ്ഞു വരുന്ന സന്ദര്‍ഭങ്ങളില്‍ ടണലിങിനുള്ള സംഭാവ്യത പരമാവധിയായിരിക്കും. ടണല്‍ ചെയ്ത് പുറത്തുവരുന്ന കണികയുടെ ഊര്‍ജം E തന്നെയായിരിക്കുകയും ചെയ്യും.
മറ്റൊരുദാഹരണത്തിലൂടെ ഇത് കൂടുതല്‍ വിശദീകരിക്കാം. ഉയരമുള്ള മലമുകളിലേക്ക് അതിന്റെ ചരിവിലൂടെ ഒരുപന്തുരുട്ടി വിട്ടാല്‍ പന്തിന്റെ സ്ഥാനംകൊണ്ട് അതിന് ലഭിക്കുന്ന ഗുരുത്വാകര്‍ഷണ പൊട്ടന്‍ഷ്യല്‍ ഊര്‍ജം പന്തിന്റെ മൊത്തം ഊര്‍ജത്തോടു തുല്യമാകുന്നതുവരെ പന്ത് മലമുകളിലേക്കുരുണ്ടു നീങ്ങുന്നു. ഊര്‍ജങ്ങള്‍ തുല്യമായാലുടന്‍ പന്ത് തിരിച്ചു പുറപ്പെട്ട സ്ഥാനത്തെ ലക്ഷ്യമാക്കി കീഴ്പ്പോട്ടുരുണ്ടു തുടങ്ങും. പന്തിന് മല കടന്ന് മറു വശത്തേക്കു പോകണമെങ്കില്‍ മലമുകളില്‍ അനുഭവപ്പെടുന്ന ഗുരുത്വാകര്‍ഷണ പൊട്ടന്‍ഷ്യല്‍ ഊര്‍ജത്തെ തരണം ചെയ്യാനുള്ള ഊര്‍ജം ലഭ്യമാവണം; അല്ലാതെ ഇടയ്ക്കുവച്ച് മല തുരന്ന് പന്തിന് മറുഭാഗത്തേക്കു പോകാനാവില്ല. ഈ ക്ലാസിക്കല്‍ സമീപനരീതിയെ അപേക്ഷിച്ച് തികച്ചും വിഭിന്നമാണ് ക്വാണ്ടം ബലതന്ത്രസമീപനം. ഇതുപ്രകാരം പന്തിന് മല തുരന്ന് മറുവശത്തേക്കും വേണമെങ്കില്‍ പോകാം. അതിനുള്ള സംഭാവ്യത വളരെ ചെറുതാ ണെങ്കിലും പൂജ്യമല്ല. പദാര്‍ഥത്തിന്റെ മാനങ്ങള്‍ വര്‍ധിക്കുന്തോറുമോ അതിനെ നഗ്നനേത്രങ്ങളാല്‍ എളുപ്പത്തില്‍ കാണാനാവുന്തോറുമോ പ്രസ്തുത സംഭാവ്യതയുടെ അളവ് കുറഞ്ഞു വരുന്നു. മറിച്ച് സൂക്ഷ്മാതീതമാനങ്ങളാണ് പദാര്‍ഥത്തിനെങ്കില്‍ (ഉദാ: ആല്‍ഫാ കണികകള്‍, ന്യയൂക്ലിയോണുകള്‍, ഇലക്ട്രോണുകള്‍) ടണലിങ് സംഭാവ്യത വളരെ ഉയര്‍ന്നതായിരിക്കും.
ടണലിങ് പ്രതിഭാസത്തിലേക്ക് ശ്രദ്ധയാകര്‍ഷിച്ച പ്രഥമ സംഭവം ആല്‍ഫാ കണികാ റേഡിയോ ആക്റ്റിവിറ്റിയാണ്. അണുകേന്ദ്ര ബലത്തെ അതിജീവിച്ചു പുറത്തുവരുന്ന ആല്‍ഫാ കണികകളുടെ ഊര്‍ജം അണുകേന്ദ്ര ബലത്തെ അപേക്ഷിച്ച് തുലോം ചെറുതാണ്. അതുപോലെ എല്ലാത്തരം ആല്‍ഫാ ഉത്സര്‍ജനങ്ങളുടേയും ഊര്‍ജം 2-8 മെഗ ഇലക്ട്രോണ്‍ വോള്‍ട്ട് പരിധിയില്‍പ്പെടുമ്പോള്‍ പ്രസ്തുത ഉത്സര്‍ജനത്തിന് ജന്മം നല്‍കുന്ന അണുകേന്ദ്രങ്ങളുടെ ആയുര്‍ദൈര്‍ഘ്യത്തിന്റെ മൂല്യം 1011 വര്‍ഷം- 10-6സെ. പരിധിയിലാണ് വരുന്നത്; അതായത് 4 മടങ്ങ് ഊര്‍ജവ്യത്യാസം 1024 മടങ്ങ് ആയുര്‍ദൈര്‍ഘ്യ വ്യതിയാനം സൃഷ്ടി ക്കുന്നു. ഇത്തരം പ്രതിഭാസങ്ങള്‍ വിശദമാക്കാന്‍ ടണലിങ് സിദ്ധാന്തത്തിനേ കഴിയുകയുള്ളു.
ടണലിങ് പ്രതിഭാസത്തെ അടിസ്ഥാനമാക്കി പ്രവര്‍ത്തിച്ച് പ്രതലങ്ങളുടെ സ്ഥാനീയ ചാലകത മാപനം ചെയ്യാനുപയോഗിക്കുന്ന ഒരുപകരണമാണ് സ്കാനിങ് ടണലിങ് സൂക്ഷ്മദര്‍ശിനി (STM). സൂക്ഷ്മദര്‍ശിനിയെ ഒരു പ്രതലത്തിലൂടെ ചലിപ്പിക്കുമ്പോള്‍ ഉപകരണത്തിലെ ടണലിങ് ധാരയില്‍ അനുഭവപ്പെടുന്ന വ്യത്യാസത്തെ വിശകലനം ചെയ്യുകവഴി പ്രതലത്തിന്റെ കണികാ ഘടനയെ വ്യക്തമാക്കുന്ന പ്രതല ടൊപോഗ്രാഫിക്ക് പ്രതിബിംബം മെനഞ്ഞെടുക്കാനാകും
