This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam

സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്

ത്രികോണം

Triangle

നേര്‍വരയിലല്ലാത്ത മൂന്ന് ബിന്ദുക്കളെ ഋജുരേഖാഖണ്ഡങ്ങളുപയോഗിച്ച് യോജിപ്പിക്കുമ്പോള്‍ ലഭിക്കുന്ന ജ്യാമിതീയ രൂപം. ബഹുഭുജങ്ങളില്‍ (polygons) ഏറ്റവും ലഘുരൂപമായ ത്രികോണത്തിന് മൂന്ന് വശങ്ങളും മൂന്ന് കോണങ്ങളുമാണുള്ളത്.

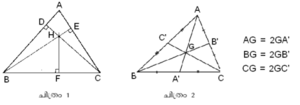
ABC എന്ന ത്രികോണത്തില്‍ (ചിത്രം 1) AB,BC,CA എന്നിവ വശങ്ങളാണ്; വശങ്ങള്‍ തമ്മില്‍ യോജിക്കുന്ന ∠A,∠B,∠ C എന്നീ ബിന്ദുക്കള്‍ ശീര്‍ഷങ്ങളും (vertices). ഇവ കോണങ്ങളാണ് (angles). ഒരു ത്രികോണത്തിന്റെ ശീര്‍ഷത്തില്‍നിന്ന് എതിര്‍വശത്തെ ഏതെങ്കിലും ബിന്ദുവിലേക്കു പതിക്കുന്ന ലംബത്തെ ഉന്നതി (altitude) എന്നു വിളിക്കുന്നു. ഇങ്ങനെ ഒരു ത്രികോണത്തിന് ആകെ മൂന്ന് ഉന്നതികള്‍ (AF,BE,DC) ഉണ്ട്. ഈ മൂന്ന് രേഖകളും സന്ധിക്കുന്ന ബിന്ദുവിനെ ലംബകേന്ദ്രം (orthocentre) എന്നു വിളിക്കുന്നു. ത്രികോണത്തിന്റെ ശീര്‍ഷങ്ങളിലൊന്നിനെ എതിര്‍വശത്തിന്റെ മധ്യബിന്ദുവുമായി യോജിപ്പിക്കുന്ന രേഖാഖണ്ഡമാണ് മധ്യമരേഖ (median). ഒരു ത്രികോണത്തിലെ മൂന്ന് മധ്യമരേഖകളും സന്ധിക്കുന്ന ബിന്ദുവാണ് കേന്ദ്രകം (centroid). കേന്ദ്രകത്തില്‍നിന്ന് ശീര്‍ഷത്തിലേക്കുള്ള അകലം, കേന്ദ്രകത്തില്‍നിന്ന് ആധാരത്തിലേക്കുള്ള അകലത്തിന്റെ ഇരട്ടിയായിരിക്കും (ചിത്രം 2).

ഒരു ത്രികോണത്തിന്റെ ശീര്‍ഷങ്ങളെ സ്പര്‍ശിച്ചുകൊണ്ട് വരയ്ക്കുന്ന വൃത്തത്തിന്റെ കേന്ദ്രത്തെ ത്രികോണത്തിന്റെ പരികേന്ദ്രം (circumcentre) എന്നു വിളിക്കുന്നു (ചിത്രം 3). ത്രികോണങ്ങളില്‍ ലംബകേന്ദ്രം, കേന്ദ്രകം, പരികേന്ദ്രം എന്നിവ ഒരേ ഋജുരേഖയില്‍ത്തന്നെയായിരിക്കും എന്ന് സ്വിസ് ഗണിതശാസ്ത്രജ്ഞനായ ലിയോനാഡ് ഓയ്ലര്‍ സിദ്ധാന്തിക്കുന്നു (1765). ഈ ഋജുരേഖ ഓയ്ലര്‍ രേഖ എന്നാണറിയപ്പെടുന്നത്.

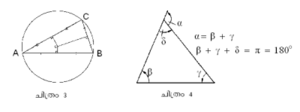
ത്രികോണത്തിലെ വശങ്ങള്‍ ഉള്‍ക്കൊള്ളുന്ന കോണങ്ങളാണ് ആന്തര കോണങ്ങള്‍ (interior angles ചിത്രത്തില്‍ ∠A, ∠B,∠C). ഈ മൂന്ന് കോണങ്ങളുടെയും ആകെ തുക 180° ആയിരിക്കും. വശങ്ങള്‍ നീട്ടിയാല്‍ അവ സമീപവശവുമായി ഉണ്ടാക്കുന്ന കോണങ്ങളാണ് ബാഹ്യകോണങ്ങള്‍ (exterior angles). ഒരു ആന്തര കോണത്തിന്റെയും ഒരു ബാഹ്യ കോണത്തിന്റെയും ആകെത്തുക 180° ആയിരിക്കും.

മൂന്ന് ആന്തര കോണങ്ങളുടെയും സമഭാജികള്‍ ഖണ്ഡിക്കുന്ന ബിന്ദുവിനെ അന്തഃകേന്ദ്രം (incentre) എന്നു പറയുന്നു. ഏതെങ്കിലും ഒരു ശീര്‍ഷത്തിലുള്ള ബാഹ്യകോണത്തിന്റെ മൂല്യം ഇതരശീര്‍ഷങ്ങളിലെ ആന്തര കോണങ്ങളുടെ തുകയ്ക്കു തുല്യമാണ് (ചിത്രം 4).

ത്രികോണങ്ങളെ അവ രൂപപ്പെട്ടിരിക്കുന്ന പ്രതലത്തിനനുസരിച്ച് സമതല ത്രികോണം, ഗോളീയ ത്രികോണം, വക്രരേഖീയ ത്രികോണം എന്നിങ്ങനെ വര്‍ഗീകരിക്കാം.

1. സമതല ത്രികോണം (Plane triangle). ഒരു സമതലത്തില്‍ മൂന്ന് രേഖകള്‍ തമ്മില്‍ ഖണ്ഡിക്കുമ്പോള്‍ സമതല ത്രികോണം രൂപംകൊള്ളുന്നു. വശങ്ങളുടെ അടിസ്ഥാനത്തില്‍ സമതലത്രികോണങ്ങളെ മൂന്നായി തരംതിരിക്കാവുന്നതാണ്. രണ്ട് വശങ്ങള്‍ തുല്യമായ സമദ്വിഭുജ ത്രികോണം (isosceles triangle), മൂന്ന് വശങ്ങളും വ്യത്യസ്തമായ വിഷമഭുജ ത്രികോണം (scalene triangle), മൂന്ന് വശങ്ങളും തുല്യമായ സമപാര്‍ശ്വ ത്രികോണം (equilateral triangle) എന്നിവയാണ് അവ. കോണങ്ങളുടെ അടിസ്ഥാനത്തിലും സമതല ത്രികോണങ്ങളെ വര്‍ഗീകരിക്കാറുണ്ട്. ഒരു കോണം 90° ആയ മട്ട ത്രികോണം (right angled triangle), ഒരു കോണവും 90° അല്ലാത്ത തിര്യക്കോണ ത്രികോണം (oblique angled triangle) എന്നിങ്ങനെയാണ് ആ വര്‍ഗീകരണം.

തിര്യക്കോണ ത്രികോണങ്ങള്‍ രണ്ട് വിധത്തിലുണ്ട്.

1. മൂന്ന് കോണങ്ങളും 90° യില്‍ കുറവായിട്ടുള്ള ന്യൂനകോണ ത്രികോണം (acute angled triangle).

2. ഏതെങ്കിലും ഒരു കോണത്തിന്റെ അളവ് 90°ക്കും 180°ക്കും ഇടയ്ക്കുള്ള അധികകോണ ത്രികോണം (obtuse angled triangle).

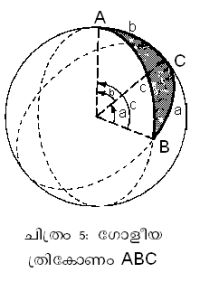
2. ഗോളീയ ത്രികോണം (spherical triangle). ഒരു ഗോളത്തിന്റെ പ്രതലത്തില്‍ മൂന്ന് മഹാവൃത്തങ്ങള്‍ (Great circles) പരസ്പരം ഖണ്ഡിക്കുമ്പോള്‍ ഉണ്ടാകുന്ന ത്രികോണമാണ് ഗോളീയ ത്രികോണം (ചിത്രം 5). ഇവിടെ വക്രരേഖകളായ ചാപങ്ങളാണ് ത്രികോണവശങ്ങളായി വരുന്നത്. രണ്ട് ചാപങ്ങള്‍ അന്യോന്യം ഖണ്ഡിക്കുന്ന ബിന്ദുക്കള്‍ ഗോളീയ ത്രികോണത്തിന്റെ ശീര്‍ഷങ്ങളാകുന്നു. ഗോളീയ ത്രികോണത്തിലെ മൂന്ന് കോണങ്ങളുടെയും (ഗോളീയ കോണങ്ങള്‍) തുക 180°ക്കും 540°ക്കും ഇടയ്ക്കായിരിക്കും.

ഈ ത്രികോണങ്ങളെ പ്രധാനമായും ആറായി തരംതിരിക്കാം.

1. ഒരു കോണം മട്ടകോണമായ ഏകസമകോണീയ ഗോളീയ ത്രികോണം (right spherical triangle)

2. രണ്ട് കോണങ്ങള്‍ മട്ടകോണങ്ങളായ ദ്വിസമകോണീയ (birectangular) ഗോളീയ ത്രികോണം

3. മൂന്ന് കോണങ്ങളും മട്ടകോണങ്ങളായ ത്രിസമകോണീയ (trirectangular) ഗോളീയ ത്രികോണം

4. ഒരു കോണവും 90° അല്ലാത്ത തിര്യക് ഗോളീയ ത്രികോണം

5. രണ്ട് വശങ്ങള്‍ തുല്യമായ സമദ്വിഭുജ ഗോളീയ ത്രികോണം

6. മൂന്ന് വശങ്ങളും വ്യത്യസ്തമായ വിഷമഭുജ ഗോളീയത്രികോണം.

ഗോളീയ ത്രികോണാശയങ്ങള്‍ ഏറെയും പ്രയോജനപ്പെടുന്നത് ജ്യോതിശ്ശാസ്ത്രം, നാവികം തുടങ്ങിയ മേഖലകളിലാണ്.

3. വക്രരേഖീയ ത്രികോണം (Curvilinear triangle). ഒരു ത്രികോണത്തിന്റെ മൂന്ന് വശങ്ങളും വക്രരേഖകളാണെങ്കില്‍ അത്തരം ത്രികോണങ്ങളാണ് വക്രരേഖീയ ത്രികോണങ്ങള്‍.

ത്രികോണങ്ങളുടെ വിസ്തീര്‍ണം. സമതല ത്രികോണങ്ങളുടെ വിസ്തീര്‍ണം,

A = ½bh (b = ആധാര നീളം , h = ശീര്‍ഷലംബ നീളം) എന്ന സൂത്രവാക്യമുപയോഗിച്ചാണ് നിര്‍ണയിക്കുന്നത്.a,b,c എന്നിവ മൂന്ന് വ്യത്യസ്ത വശങ്ങളായിരിക്കുമ്പോള്‍

ത്രികോണങ്ങളെയും ത്രികോണമിതീയ ഫലനങ്ങളെയും (trigonometric function) അവയുടെ പ്രയോഗങ്ങളെയും കുറിച്ചുള്ള ഗണിതശാഖയാണ് ത്രികോണമിതി (Trigonometry).