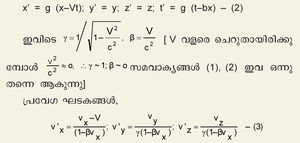This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ആപേക്ഷികതാ സിദ്ധാന്തം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
ഉള്ളടക്കം |
ആപേക്ഷികതാ സിദ്ധാന്തം
Theory of Relativity
സ്ഥലം, കാലം ഇവയെ ബന്ധിപ്പിച്ചുകൊണ്ട് ആല്ബര്ട്ട് ഐന്സ്റ്റൈന് അവതരിപ്പിച്ച പുതിയ ഭൌതിക സിദ്ധാന്തം. 1905-ല് ഐന്സ്റ്റൈന് അവതരിപ്പിച്ച വിശേഷ ആപേക്ഷികതാ സിദ്ധാന്തം ത്രിമാനങ്ങളുള്ള സ്ഥലത്തെയും ഏകമാനമുള്ള കാലത്തെയും ഏകീകരിച്ച് പരന്ന (flat) ചതുര്മാന 'സ്ഥല-കാല സാതത്യ'ത്തിന് (space time Continuum) ജന്മം നല്കി. 1915-ല് അതു വക്രമായ സ്ഥലകാലത്തിലേക്ക് വികസിപ്പിക്കുകയും ഗുരുത്വ ബലത്തെ സ്ഥല-കാല വക്രതയുമായി ബന്ധിപ്പിക്കുകയും ചെയ്തു. ഇതു സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം എന്നറിയപ്പെടുന്നു. 1632-ല് ഗലീലിയോ ആവിഷ്കരിച്ച ആപേക്ഷികതാതത്ത്വത്തിന്റെ തുടര്ച്ച തന്നെയാണ് ഐന്സ്റ്റൈന്റെ സിദ്ധാന്തവും.
ഗലീലിയന് ആപേക്ഷികത
ത്വരണമില്ലാതെ, പരസ്പരം സമവേഗത്തില് ചലിക്കുന്ന ആധാരവ്യവസ്ഥകളെയെല്ലാം ഗലീലിയോ ജഡാധാര വ്യവസ്ഥകള് (Intertial frames of reference) എന്നുവിളിച്ചു. ബലതന്ത്രത്തിലെ നിയമങ്ങളെല്ലാം എല്ലാ ജഡാധാര വ്യവസ്ഥകളിലെ നിരീക്ഷകര്ക്കും ഒരുപോലെയാണ് അനുഭവപ്പെടുക എന്നതാണ് ഗലീലിയോയുടെ ആപേക്ഷികതാ തത്ത്വം. ഈ തത്ത്വത്തെ പൂര്ണമായി വികസിപ്പിച്ചത് ഐസക് ന്യൂട്ടണ് ആയതുകൊണ്ട് ഇത് ന്യൂട്ടന്റെ ആപേക്ഷികതാ തത്ത്വം എന്നും അറിയപ്പെടുന്നു.
നിശ്ചല ജലത്തില് സ്ഥിതിചെയ്യുന്ന ഒരു കപ്പലില് ഇരുന്നുകൊണ്ട് മറ്റൊരു കപ്പല് നിരീക്ഷിക്കുന്ന ആള്ക്ക് അവ ആപേക്ഷികമായി ചലിക്കുന്നുണ്ടോ ഇല്ലയോ എന്നേ പറയാന് പറ്റൂ; തന്റെ കപ്പലിനുള്ളില് വച്ചു നടത്തുന്ന ഒരു ഭൌതികപരീക്ഷണം വഴിയും ഏതു കപ്പലാണ് 'യഥാര്ഥത്തില്' ചലിക്കുന്നത് എന്ന് നിര്ണയിക്കാനാവില്ല-ഇതാണ് ആപേക്ഷികതാ തത്ത്വത്തിന്റെ ഉള്ളടക്കം. സമയത്തെ കേവലം (ആധാര വ്യവസ്ഥാ നിരപേക്ഷം) ആയാണ് ഗലീലിയോയും ന്യൂട്ടണും പരിഗണിച്ചത്.
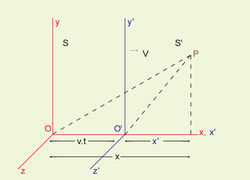
S(x,y,z),S'(x',y',z') എന്നീ രണ്ട് കാര്ട്ടീഷ്യന് ആധാരവ്യവസ്ഥകളെ സങ്കല്പിക്കുക. പ്രാരംഭത്തില് (t=0) O, O' എന്നീ മൂലബിന്ദുക്കള് ഒരിടത്തായിരുന്നു. S',x ദിശയില്, V വേഗത്തില് ചലിക്കുന്നുവെങ്കില് t സമയത്തിനുശേഷം O-O' ദൂരം= V.t ആയിരിക്കുമല്ലൊ. P എന്ന ബിന്ദുവില് നടക്കുന്ന ഒരു സംഭവത്തിന്റെ സ്ഥാനവും സമയവും S ലും S' ലും ഉള്ള നിരീക്ഷകര് രേഖപ്പെടുത്തുക ഇപ്രകാരമായിരിക്കും:
S ലെ നിരീക്ഷകന്: P=P(x,y,z,t)
S' ലെ നിരീക്ഷകന്: P=P(x',y',z',t')
S' ന്റെ ചലനം x ദിശയില് ആയതിനാല്,
x'=x-Vt;y=y;z'=z;t'=t-(1)
ഇതാണ് ഗലീലിയന് പരിവര്ത്തനസമവാക്യങ്ങള് (Galilean transformation equations) എന്നറിയപ്പെടുന്നത്. ഇതില്നിന്ന് P യുടെ പ്രവേഗത്തിന്റെ ഘടകങ്ങള് ഇങ്ങനെ കിട്ടും
v'x = vx - V, v'y = vy;v'z = vz
അതുപോലെ ത്വരണം
(ഇവിടെ vx dx/dt, ax dvx/dt തുടങ്ങിയ ഗണിതബന്ധങ്ങള് ഉപയോഗിച്ചിരിക്കുന്നു)
വിശേഷ ആപേക്ഷികത (Special Theory of Relativity)
ഗലീലിയന് ആപേക്ഷികതയിൽ ഐന്സ്റ്റൈന് രണ്ടു പരിഷ്കരണങ്ങള് വരുത്തി. എല്ലാ ജഡാധാര വ്യവസ്ഥകളിലും ബലതന്ത്ര നിയമങ്ങള്ക്ക് ഒരേ രൂപമായിരിക്കും എന്നതിനുപകരം ഭൗതികനിയമങ്ങള്ക്കെല്ലാം (വിദ്യുത് കാന്തിക നിയമങ്ങള് ഉള്പ്പെടെ) ഒരേ രൂപമായിരിക്കും എന്നു മാറ്റി. കൂടാതെ, എല്ലാ ജഡാധാര വ്യവസ്ഥകളിലും ശൂന്യതയിലെ പ്രകാശത്തിന്റെ പ്രവേഗം (c) ഒന്നുതന്നെ ആയിരിക്കും എന്ന ഒരു പുതിയ തത്ത്വം കൂട്ടിച്ചേർക്കുകയും ചെയ്തു. ഇതിന്റെ ഫലമായി മുന് സമവാക്യങ്ങള് ഈ വിധം മാറ്റേണ്ടിവന്നു. (പുതിയ സമവാക്യങ്ങള് ലോറന്റ്സ് പരിവർത്തന സമവാക്യങ്ങള് എന്നറിയപ്പെടുന്നു).
ലോറന്റ്സ് പരിവർത്തന സമവാക്യങ്ങളിൽ നിന്ന് നിർധരിച്ചെടുത്ത ചില നിഗമനങ്ങള് സാമാന്യ ബുദ്ധിക്കു നിരക്കാത്തവയും ശാസ്ത്രലോകത്തെ ഞെട്ടിച്ചവയും ആയിരുന്നു.
1. നീളത്തിന്റെ ചുരുങ്ങലും സമയത്തിന്റെ ദീർഘീകരണവും. S എന്ന ജഡാധാര വ്യവസ്ഥയിൽ Lo നീളമുള്ള ഒരു ദണ്ഡ് x- ദിശയിൽ വച്ചിരിക്കുന്നു എന്നിരിക്കട്ടെ. V വേഗത്തിൽ +x ദിശയിൽ സഞ്ചരിക്കുന്ന S എന്ന വ്യവസ്ഥയിൽ നിന്ന് നിരീക്ഷിക്കുന്ന ഒരാള് അതിന്റെ നീളം അളന്നാൽ കിട്ടുക L= എന്നായിരിക്കും. ഉദാ: V = 0.8c ആണെന്നിരിക്കട്ടെ. ഇതിൽനിന്ന് L= 0.6 Lo എന്നുകിട്ടുന്നു. ഇതുപോലെ, S എന്ന ജഡാധാര വ്യവസ്ഥയിൽ നടക്കുന്ന രണ്ടു സംഭവങ്ങളുടെ സമയാന്തരാളം t2 - t1 = t0 എന്ന് അതിലെ നിരീക്ഷകർ അളക്കുമ്പോള്, അതേ സമയാന്തരാളം S' ലെ നിരീക്ഷകന് അളക്കുക t'=gt0 എന്നായിരിക്കും. അതായത് സംഭവങ്ങള്ക്കിടയിലെ സമയാന്തരാളം കൂടുന്നതായി, അഥവാ സമയം മന്ദഗതിയിലാകുന്നതായി അയാള്ക്ക് അനുഭവപ്പെടുന്നു.
സമകാലികതയുടെ ആപേക്ഷികത
S വ്യവസ്ഥയിൽ ഉള്ള ഒരു നിരീക്ഷകന് x1,x2 എന്ന രണ്ട് സ്ഥാനങ്ങളിൽ നടക്കുന്ന രണ്ടു സംഭവങ്ങളെ ഒരേ സമയത്ത് കാണുന്നുവെങ്കിൽ അയാള്ക്ക് ആ സംഭവങ്ങള് സമകാലികങ്ങള് (Simultaneous) ആണ്. എന്നാൽ S' ലെ നിരീക്ഷകന് അവ സമകാലികമാകണമെന്നില്ല എന്ന് സമവാക്യം (2) പരിശോധിച്ചാൽ മനസ്സിലാകും.
പിണ്ഡത്തിന്റെ ആപേക്ഷികത
ഒരു ജഡാധാര വ്യവസ്ഥയിൽ നിശ്ചലമായിരിക്കുന്ന ഒരു വസ്തുവിന്റെ പിണ്ഡത്തെ (m0 അതിന്റെ നിശ്ചല പിണ്ഡം എന്നു വിളിക്കുന്നു. V വേഗത്തിൽ വസ്തു ചലിക്കുമ്പോള് (അല്ലെങ്കിൽ V വേഗത്തിൽ നിരീക്ഷകന്റെ ആധാരവ്യവസ്ഥ ചലിച്ചാലും മതി). അതിന്റെ പിണ്ഡം m= g m0 ആയിരിക്കും. ഉദാ. 0.8c വേഗത്തിൽ സഞ്ചരിക്കുന്ന വസ്തുവിന്റെ പിണ്ഡം 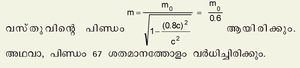
പദാർഥ ഊർജ സർവസമത
ഒരു വസ്തുവിന്റെ വേഗത വർധിക്കുംതോറും അതിന്റെ പിണ്ഡവും വർധിക്കുന്നു എന്നതിനർഥം ചെലവിടുന്ന ഊർജം പദാർഥമായി മാറുന്നു എന്നാണല്ലോ. ഇതിൽനിന്ന് ഐന്സ്റ്റൈന് എത്തിയ നിഗമനം ഇതാണ്: പദാർഥത്തിന്റെ പിണ്ഡത്തെയും ഊർജത്തെയും രണ്ടായി കാണേണ്ടതില്ല; രണ്ടും സർവസമമാണ്. m പിണ്ഡം, E=mc2 ഊർജത്തിനു തുല്യമാണ്. ഭൗതിക ശാസ്ത്രത്തിൽ കോളിളക്കം സൃഷ്ടിച്ച ഈ സമവാക്യമാണ് ജ്യോതിശ്ശാസ്ത്രത്തിലും ഏറെ പ്രധാനമായ "ഫ്യൂഷന്',"ഫിഷന്' തുടങ്ങിയ പ്രതിമാസങ്ങളുടെ അടിസ്ഥാനം.
സ്ഥല-കാല ജ്യാമിതി
ഹെർമന് മിന്കോവ്സ്കി എന്ന ജർമന് ഗണിതജ്ഞന് സ്ഥലത്തെയും കാലത്തെയും സംബന്ധിച്ച ഒരു പുതിയ കാഴ്ചപ്പാട് രൂപപ്പെടുത്തുകയും അങ്ങനെ ഐന്സ്റ്റൈന് ആപേക്ഷികതാ സിദ്ധാന്തത്തിന്റെ ഗണിതശാസ്ത്രപരമായ അടിത്തറ ശക്തിപ്പെടുത്തുകയും ചെയ്തു.ഐന്സ്റ്റൈനു മുമ്പ് സ്ഥലവും കാലവും വ്യത്യസ്തവും കേവലവുമായി കരുതപ്പെട്ടിരുന്നു. പക്ഷേ ഇവയെ കൂട്ടിയിണക്കി ഒരു സ്ഥലകാല സാതത്യം (Space-time Continuum) ആയി പരിഗണിച്ചാൽ ലോറന്റ്സിന്റെയും ഐന്സ്റ്റൈന്റെയും സിദ്ധാന്തങ്ങള്ക്കു സ്ഫടിക തുല്യമായ വ്യക്തതയുണ്ടാകുമെന്ന് മിന്കോവ്സ്കി കണ്ടെത്തി. പിന്നീട് ഐന്സ്റ്റൈനു തന്റെ സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം വികസിപ്പിക്കാന് ഇവ വളരെയേറെ സഹായകമായി.
ഒരു പ്രകാശ കണം ഒരു സ്ഥാനത്തുനിന്നും ഒരു നിമിഷം പുറപ്പെട്ട് മറ്റൊരു സ്ഥാനത്ത് വേറൊരു നിമിഷം എത്തി എന്നു കരുതുക. ഈ രണ്ടു സംഭവങ്ങളെയും നിരീക്ഷിക്കുന്ന ഒരു നിരീക്ഷകന് "സഞ്ചരിച്ച ദൂരം' ഇങ്ങനെ എഴുതാം:
Δx cΔt
Δx എന്നത് നിരീക്ഷകന്റെ ജഡാധാരവ്യവസ്ഥയിൽ പ്രകാശം സഞ്ചരിച്ച ദൂരവും അതിനെടുത്ത സമയവും c പ്രകാശ പ്രവേഗവുമാണ്. ഇനി ഈ നിരീക്ഷകനുമായി സമആപേക്ഷികചലനത്തിലുള്ള(Uniform relative motion)മറ്റൊരു നിരീക്ഷകനെ സങ്കല്പിക്കുക. ഇവർ സഞ്ചരിക്കുന്നത് പൊതുവായ x ദിശയിലാണെന്നിരിക്കട്ടെ. വിശേഷ ആപേക്ഷികതാ സിദ്ധാന്തപ്രകാരം പ്രകാശവേഗം c സ്ഥിരമായതുകൊണ്ട് രണ്ടാമത്തെ നിരീക്ഷകന് മുകളിൽ പറഞ്ഞ സമവാക്യം എഴുതേണ്ടത് എന്നാണ്.
പ്രകാശം ഇവരുടെ പൊതുവായ x ദിശയിലല്ല സഞ്ചരിച്ചതെങ്കിൽ x,y,z എന്നീ മൂന്ന് ചരങ്ങളും കണക്കിലെടുക്കേണ്ടിവരും. അപ്പോള് മേല്പറഞ്ഞ സമവാക്യങ്ങള് എഴുതേണ്ടത് ഇപ്രകാരമായിരിക്കും.
ഒരു പ്രകാശരശ്മിയുടെ വികിരണവും എത്തിച്ചേരലുമാണിവിടെ രണ്ടു സംവങ്ങളായി എടുത്തത്. ഏതു രണ്ടു സംഭവങ്ങള്ക്കും ഈ സമവാക്യം ബാധകമാകുമെന്ന് സങ്കല്പിച്ചാൽ അതിൽനിന്നും നമുക്കു വിശേഷ ആപേക്ഷികത സിദ്ധിക്കാന് കഴിയും.
സമവാക്യം (6) സ്ഥലകാലത്തെ സംബന്ധിക്കുന്ന പൈതഗോറസ് തിയറമായി പരിഗണിക്കാം എന്നാണ് മിങ്കോവ്സ്കി കണ്ടെത്തിയത്. രണ്ടു വ്യത്യസ്ത നിരീക്ഷകർക്ക്, അവർ ആപേക്ഷികമായി സഞ്ചരിച്ചു കൊണ്ടിരിക്കുമ്പോള്, ദൂരവും സമയദൈർഘ്യവും ഒറ്റയ്ക്കൊറ്റയ്ക്കു കേവലമായിരിക്കണമെന്നു നിർബന്ധമില്ല. രണ്ടു സംഭവങ്ങള്ക്കിടയിലെ ദൂരം വ്യത്യസ്തമായി അനുഭവപ്പെടുമ്പോള് അതനുസരിച്ച് സമയദൈർഘ്യവും വ്യത്യസ്തമായാൽ മതി എന്നാണ് സമവാക്യം (6) പറയുന്നത്. സ്ഥലകാല സാതത്യത്തിലെ ഒരിടവേള Δ,എല്ലാ നിരീക്ഷകർക്കും ഒന്നുതന്നെയായിരിക്കണം എന്നുള്ളതാണ് പ്രധാന സംഗതി.
Δs2 = c2Δt2 - (Δx2+Δy2+Δz2) = c2Δt'2 - (Δx'2+Δy'2+Δz'2) -(7)
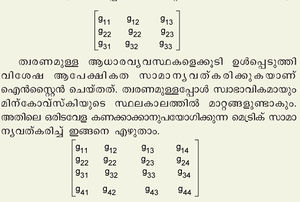
ആപേക്ഷികതാ സിദ്ധാന്തത്തിൽ സ്ഥലവും കാലവും ആപേക്ഷികമാണെങ്കിലും സ്ഥലകാല സാതത്യത്തിലെ ഇടവേളയായ ഉ ആെപേക്ഷികമല്ല, കേവലമാണെന്ന് മിന്കോവ്സ്കി കണ്ടെത്തി. സാധാരണ പൈതഗോറസ് സിദ്ധാന്തത്തിൽ (Δt2 = Δx2+Δy2+Δz2,c=1 എന്നെടുത്തിരിക്കുന്നു.) Δt2 കണ്ടുപിടിക്കാന് വേണ്ട ഘടകങ്ങളുടെ കൂട്ടത്തിൽ ΔxΔy, ΔxΔz, ΔyΔz തുടങ്ങിയവ വരുന്നില്ല. Δx2, Δy2, Δz2 എന്നിവയ്ക്ക് ഗുണകങ്ങളായി വരുന്ന സംഖ്യ ഒന്ന് (1) ആണ്. വരാത്തവയുടെ ഗുണകങ്ങളെ പൂജ്യം (0) എന്നു രേഖപ്പെടുത്താമെങ്കിൽ ഈ ഒന്പത് ഗുണകങ്ങളെ താഴെക്കാണിച്ചിരിക്കുന്നതുപോലെ ചിട്ടയായി എഴുതാന് കഴിയും.
ഇത്തരം മെട്രിക്കാണ് സ്ഥലകാലത്തിന്റെ ജ്യാമിതി നിശ്ചയിക്കുന്നത്.
സാമാന്യ ആപേക്ഷികതാസിദ്ധാന്തം
(General Theory of Relativity). 1915-ലാണ് ആൽബർട്ട് ഐന്സ്റ്റൈന് സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം അവതരിപ്പിക്കുന്നത്. വിശേഷ ആപേക്ഷികതയുടെ സാമാന്യവത്കരണമായാണ് ഇത് നിർദേശിക്കപ്പെട്ടത്. എങ്കിലും ഗുരുത്വാകർഷണത്തെപ്പറ്റിയുള്ള ഒരു നൂതന സിദ്ധാന്തമായി ഇതു രൂപാന്തരപ്പെട്ടു.
ഒരു വസ്തു മറ്റൊന്നിൽ പ്രയോഗിക്കുന്ന ബലം എന്ന ന്യൂട്ടന്റെ ഗുരുത്വാകർഷണ തത്ത്വത്തിൽനിന്നു വ്യത്യസ്തമായി സ്ഥലകാലത്തിന്റെ വക്രതമൂലം വസ്തുക്കളിലെ പാതയിലുണ്ടാകുന്ന വ്യതിയാനമായി ഗുരുത്വാകർഷണത്തെ ചിത്രീകരിക്കുകയാണ് ഐന്സ്റ്റൈന് ചെയ്തത്. ശക്തികുറഞ്ഞ ഗുരുത്വാകർഷണമേഖലകളിൽ സാമാന്യ ആപേക്ഷികതയും ന്യൂട്ടന്റെ നിയമവും ഒരേ ഫലം തന്നെ തരുമ്പോള് ഗുരുത്വബലം ശക്തമായ മേഖലകളിൽ സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം മാത്രമാണ് ശരിയായ ഉത്തരങ്ങള് തരാന് പ്രാപ്തമായത്.
മിന്കോവ്സ്കിയുടെ സ്ഥലകാലം യൂക്ലിഡിയനല്ലെങ്കിലും വക്രമല്ല. വക്രതലത്തിന് ഉദാഹരണമാണ് ഒരു ഗോളത്തിന്റെ ഉപരിതലം. ഇതൊരു ദ്വിമാനതലമാണ്. ഇതിലെ ഏതെങ്കിലുമൊരു ബിന്ദുവിനെ സൂചിപ്പിക്കാന് രണ്ടുചരങ്ങള് നല്കിയാൽ മതി. ഭൂമിയുടെ ഉപരിതലത്തിൽ ഒരു നഗരത്തെ സൂചിപ്പിക്കാന് അതിന്റെ അക്ഷാംശവും രേഖാംശവും മതിയല്ലോ.
യൂക്ലിഡിയന് അല്ലാത്ത, വക്രതലത്തിലെ ദൂരം കണക്കാക്കാന് ബേർണാർഡ് റീമാന് പൈതഗോറസ് തിയറത്തിൽ മാറ്റം വരുത്തി; Δt2 = Δx2+Δy2+Δz2 എന്നതിനുപകരം ΔxΔy, ΔxΔz, ΔyΔz തുടങ്ങിയ എല്ലാ ഘടകങ്ങളുമുള്പ്പെടുത്തി,
Δt2 = g11Δx2 + g12ΔxΔy + g13ΔxΔz + g21ΔyΔx + g22Δy2 + g23ΔyΔz + g31ΔzΔy + g33 Δz2
എന്ന് എഴുതി. അപ്പോള് അതിന്റെ മെട്രിക് ഇങ്ങനെയാകും:
ഈ സ്ഥിതിയിൽ ഇതൊരു വക്രമായ സ്ഥലകാലമായിരിക്കും. ഇത് ഗുരുത്വാകർഷണത്തെപ്പറ്റിയുള്ള സിദ്ധാന്തമാക്കി മാറ്റാന്വേണ്ടി ഐന്സ്റ്റൈന് ഒരു സർവസമതാ തത്ത്വത്തിനു (equivalence principle) രൂപംനല്കി. ഒരു ആധാരവ്യവസ്ഥയിൽ സ്ഥിതിചെയ്യുന്ന നിരീക്ഷകന് തന്റെ നിരീക്ഷണഫലങ്ങള് ഗുരുത്വം കാരണമാണോ അതോ ആധാരവ്യവസ്ഥയുടെ ത്വരണം മൂലമാണോ എന്ന് തിരിച്ചറിയാന് സാധ്യമല്ല എന്നാണ് ഈ തത്ത്വം പറയുന്നത്. ത്വരണമുള്ളപ്പോള് മിന്കോവ്സ്കിയുടെ സ്ഥലകാലം വക്രമായിരിക്കും എന്ന് ഐന്സ്റ്റൈന് മനസ്സിലാക്കി. എങ്കിൽ ഗുരുത്വാകർഷണ മണ്ഡലവും വക്രസ്ഥലകാലവുമായി ബന്ധപ്പെട്ടതാകണം. വളരെച്ചെറിയ സ്ഥലകാല പരിധിക്കുള്ളിൽ മാത്രമാണ് പൂർണമായ തോതിൽ സർവസമതാ തത്ത്വം ബാധകമാകുന്നത്. കാരണം ഗുരുത്വാകർഷണം പല സ്ഥലത്ത് പല അളവിലും ദിശയിലുമായിരിക്കും.
അതുകൊണ്ട് ഒരിടത്തെ ഗുരുത്വമണ്ഡലം നിർവചിക്കാന് അവിടത്തെ വക്രസ്ഥലകാലത്തിന്റെ മെട്രിക്കിലെ g11, g12 തുടങ്ങിയ ഘടകങ്ങള് കണ്ടുപിടിക്കുകയാണ് വേണ്ടത്. ഇതിനായി പൊതുആപേക്ഷികതയുടെ അടിസ്ഥാനമായ "ഐന്സ്റ്റൈന് സ്ഥിതി സമവാക്യം' (equation of state) നിർധാരണം ചെയ്യണം.
ഗുരുത്വാകർഷണത്തിലെ ന്യൂട്ടന്റെ സമവാക്യവുമായി താരതമ്യം ചെയ്താൽ ഐന്സ്റ്റൈന്റെ സമവാക്യം സങ്കീർണമാണ്. നമുക്കു കണ്ടുപിടിക്കേണ്ട മെട്രിക്കിന്റെ ഘടകങ്ങള് ഉള്പ്പെടുന്ന ടെന്സർ സമവാക്യമാണത്. ഓരോ തരത്തിലുള്ള പദാർഥ-ഊർജ ഘടനകളുടെ സാമീപ്യത്തിലും സ്ഥലകാലത്തിന്റെ മെട്രിക് ഈ സമവാക്യം നിർധാരണം ചെയ്തുകണ്ടുപിടിക്കാം. തമോഗർത്തങ്ങളെ വിശദീകരിക്കുന്ന ഷ്വാർത്സ് ചൈൽഡ് മെട്രിക്, പ്രപഞ്ച വിജ്ഞാനീയത്തിലുപയോഗിക്കുന്ന ഡി സിറ്റർ മാതൃക, സ്വയം കറങ്ങുന്ന തമോഗർത്തങ്ങളുടെ കെർ മെട്രിക് തുടങ്ങിയവ ഐന്സ്റ്റൈന് സമവാക്യത്തിന്റെ പ്രസിദ്ധങ്ങളായ നിർധാരണങ്ങളാണ്.
സാമാന്യ ആപേക്ഷികതയുടെ അനന്തരഫലങ്ങള്
സൗരസമീപക ബിന്ദുവിന്റെ പുരസ്സരണം
ഗ്രഹങ്ങളുടെ സഞ്ചാരപഥങ്ങള് ദീർഘവൃത്തങ്ങളാണ്. ഗ്രഹം സൂര്യന് ഏറ്റവും അടുത്തെത്തുമ്പോഴുള്ള അതിന്റെ സ്ഥാനത്തിന് സൗരസമീപകബിന്ദു എന്നു പറയും. ഈ ബിന്ദുവിന്റെ സ്ഥാനം മന്ദഗതിയിൽ സൂര്യനെ പ്രദക്ഷിണം വയ്ക്കുന്നതായി കാണുന്നു. സൗരയൂഥത്തിലെ ആദ്യത്തെ ഗ്രഹമായ ബുധന് ഒരു നൂറ്റാണ്ടിൽ 5600.730 ± 0.41 ആർക് സെക്കണ്ട് വീതം ഈവിധം പ്രദക്ഷിണം നടത്തുന്നു. ഇതു ന്യൂട്ടന്റെ സിദ്ധാന്തംകൊണ്ട് പൂർണമായും വിശദീകരിക്കാന് കഴിഞ്ഞിരുന്നില്ല. ഒരു നൂറ്റാണ്ടിൽ ഏതാണ്ട് 43 ആർക്സെക്കന്ണ്ട് കൂടുതലായി സംഭവിക്കുന്നതെന്തുകൊണ്ട് എന്ന അന്വേഷണത്തിലായിരുന്നു ജ്യോതിശ്ശാസ്ത്രജ്ഞർ. സാമാന്യ ആപേക്ഷികതയുപയോഗിച്ച് ഐന്സ്റ്റൈന് അത് പൂർണമായും വിശദീകരിക്കാന് കഴിഞ്ഞു. സാമാന്യ ആപേക്ഷികതയുടെ വിജയകരമായ ആദ്യപ്രയോഗമായിരുന്നു അത്.
പ്രകാശപഥത്തിന്റെ വ്യതിചലനം
ഗുരുത്വം സ്ഥലകാലത്തിന്റെ വക്രതമൂലമാണെങ്കിൽ ആ സ്ഥലകാലത്തിലെ നേർരേഖ (ജിയോഡെസിക്)യിൽക്കൂടി സഞ്ചരിക്കുന്ന പ്രകാശത്തിന്റെ പാത നമ്മുടെ നിരീക്ഷണത്തിൽ വളഞ്ഞുകാണപ്പെടേണ്ടതാണ്. ഈ പ്രവചനം ശരിയാണോ എന്നു പരിശോധിക്കുകയായിരുന്നു സാമാന്യ ആപേക്ഷികതയുടെ പ്രധാന സംശോധനം. സൂര്യന്റെ വളരെ അടുത്തുകൂടി കടന്നുവരുന്ന നക്ഷത്ര രശ്മികളെ സൂര്യഗ്രഹണസമയത്ത് നിരീക്ഷിക്കുകയും അതിന്റെ പാതയുടെ വളയൽ സാമാന്യ ആപേക്ഷികതയിൽ പ്രവചിക്കപ്പെട്ടതു തന്നെയാണോ എന്നു പരിശോധിക്കുകയും വേണ്ടിയിരുന്നു. 1919 മേയ് 20-ലെ സൂര്യഗ്രഹണസമയത്ത് ആർതർ എഡിങ്ടണും കൂട്ടരും നടത്തിയ പ്രസിദ്ധമായ നിരീക്ഷണത്തിൽ ഐന്സ്റ്റൈന്റെ പ്രവചനം ശരിവയ്ക്കുന്നതായി തെളിയിക്കപ്പെട്ടു.
പ്രകാശത്തിന്റെ ആവൃത്തിമാറ്റം
ഒരുഗുരുത്വമണ്ഡലത്തിലേക്ക് കടന്നുവരുന്ന പ്രകാശത്തിന്റെ ആവൃത്തി വർധിച്ച് നീലയുടെ ഭാഗത്തേക്കും ഗുരുത്വമണ്ഡലത്തിൽ നിന്നും പുറത്തേക്കു പോകുന്ന പ്രകാശത്തിന്റെ ആവൃത്തി കുറഞ്ഞ് ചുവപ്പിന്റെ ഭാഗത്തേക്കും നീങ്ങുന്നു എന്നത് സാമാന്യ ആപേക്ഷികതയുടെ മറ്റൊരു പ്രവചനമാണ്. പ്രകാശത്തിന്റെ സ്പെക്ട്രമെടുക്കുമ്പോള് അവയിലെ വർണരാജി രേഖകള്ക്ക് ഈ പറഞ്ഞതനുസരിച്ചുള്ള സ്ഥാനമാറ്റം ഉണ്ടാകുന്നതായി പരീക്ഷണശാലകളിൽ നടത്തിയ പരീക്ഷണങ്ങളിലും ജ്യോതിശ്ശാസ്ത്ര നിരീക്ഷണങ്ങളിലും തെളിഞ്ഞിട്ടുണ്ട്.
ഗുരുത്വമണ്ഡലത്തിലെ സമയ ദീർഘീകരണം
വിശേഷ ആപേക്ഷികതയിൽ സംഭവിക്കുന്ന സമയദീർഘീകരണം ഗുരുത്വമണ്ഡലത്തിലും സംഭവിക്കാമെന്ന് സർവസമത്വതത്ത്വത്തിൽനിന്നുതന്നെ നമുക്കൂഹിക്കാം. ആറ്റോമിക് ക്ലോക്കുകളും ഗ്ലോബൽ പൊസിഷനിങ് സിസ്റ്റ(GPS)വും മറ്റും ഉപയോഗിച്ച് ഈ പ്രവചനവും ശരിവയ്ക്കാന് കഴിഞ്ഞിട്ടുണ്ട്.
ഗുരുത്വതരംഗങ്ങള്
വിദ്യുത് കാന്തിക തരംഗങ്ങളെപ്പോലെ ഗുരുത്വതരംഗങ്ങളും ഉണ്ടാകാം എന്നത് സാമാന്യ ആപേക്ഷികതയുടെ ശക്തമായ ഒരു പ്രവചനമാണെങ്കിലും ഇന്നുവരെ അത് നേരിട്ടു നിരീക്ഷിക്കാന് കഴിഞ്ഞിട്ടില്ല. എന്നാൽ ഗുരുത്വതരംഗങ്ങളെ തിരിച്ചറിഞ്ഞ് പഠനവിധേയമാക്കുക വഴി മഹാവിസ്ഫോടനാനന്തരമുള്ള പ്രപഞ്ചത്തെക്കുറിച്ച് വ്യക്തമായി മനസ്സിലാക്കാന് സാധിക്കുമെന്ന് ജ്യോതിശ്ശാസ്ത്രജ്ഞർ അഭ്യൂഹിക്കുന്നു. അതുകൊണ്ടുതന്നെ ശാസ്ത്രലോകം ഗുരുത്വതരംഗങ്ങളെ തിരിച്ചറിയാനുള്ള സാധ്യത അന്വേഷിക്കുകയാണ്. ഇതിനായി ലോകത്തിന്റെ വിവിധ ഭാഗങ്ങളിൽ നിരവധി ഗുരുത്വതരംഗ ഡിറ്റക്ടറുകള് സ്ഥാപിച്ചിട്ടുണ്ട്. മാസച്യൂസെറ്റ്സ് ഇന്സ്റ്റിറ്റ്യൂട്ട് ഒഫ് ടെക്നോളജിയും കെൽടക്ക് സർവകലാശാലയും സംയുക്തമായി സ്ഥാപിച്ചിട്ടുള്ള ലേസർ ഇന്റർഫെറോമീറ്റർ ഗ്രാവിറ്റേഷണൽ വേവ് ഒബ്സർവേറ്ററി (LIGO) ആണ് ഇതിൽ ഏറ്റവും പ്രധാനപ്പെട്ടത്. ഖഗോള വസ്തുക്കളിൽ നിന്നും വരുന്ന ഗുരുത്വതരംഗങ്ങളെ തിരിച്ചറിയാന് നാസയും യൂറോപ്യന് സ്പെയ്സ് ഏജന്സിക്കും (LISA)സംയുക്തമായി ലേസർ ഇന്റർഫെറോമീറ്റർ സ്പെയ്സ് ആന്റിന എന്ന പേരിൽ ഒരു പദ്ധതിയും ആവിഷ്കരിച്ചിട്ടുണ്ട്. 2013-ഓടെ ഇത് പ്രവർത്തന സജ്ജമാകും.
ഗ്രാവിറ്റേഷണൽ ലെന്സ്
ഗുരുത്വാകർഷണ ക്ഷേത്രത്തിൽ പ്രകാശപഥത്തിന് വ്യതിചലനം സംഭവിക്കുന്നതിനാൽ ദ്രവ്യത്തിന്റെ അത്യധികമായ കേന്ദ്രീകരണം (ഗാലക്സിക സമൂഹം) ലെന്സ് എന്നപോലെ പ്രവർത്തിച്ച് വിദൂരസ്ഥമായ പ്രകാശസ്രോതസ്സിന്റെ പ്രതിബിംബം സൃഷ്ടിക്കാന് സാധ്യതയുണ്ട്. സാമാന്യാപേക്ഷികതാ സിദ്ധാന്തത്തിന്റെ ഈ പ്രവചനം നിരീക്ഷണങ്ങളിലൂടെ സ്ഥാപിക്കാന് കഴിഞ്ഞിരിക്കുന്നു. "ഗ്രാവിറ്റേഷണൽ ലെന്സിങ്' (Gravitational Lensing) എന്ന ഈ പ്രതിഭാസം 1979-ൽ ആദ്യമായി നിരീക്ഷിക്കുകയുണ്ടായി. ഒരു ക്വാസാറിന്റെ പ്രതിബിംബമാണ് ഇങ്ങനെ ദർശിക്കാന് കഴിഞ്ഞത്. അതിനുശേഷം നിരവധി ഗ്രാവിറ്റേഷണൽ ലെന്സുകള് നിരീക്ഷണ വിധേയമായിട്ടുണ്ട്. ദൃശ്യപ്രകാശം മാത്രമല്ല റേഡിയോ തരംഗങ്ങളും ഗാലക്സികളാൽ ഇപ്രകാരം "ഫോക്കസ്' ചെയ്യപ്പെടുന്നതായി തെളിഞ്ഞിട്ടുണ്ട്.
(മോന്സി. വി. ജോണ്)